【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修五同步课件:1.2解三角形应用举例(3课时)(共38张PPT)
文档属性
| 名称 | 【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修五同步课件:1.2解三角形应用举例(3课时)(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 843.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-26 23:37:19 | ||
图片预览





文档简介
课件38张PPT。1.2 解三角形应用举例
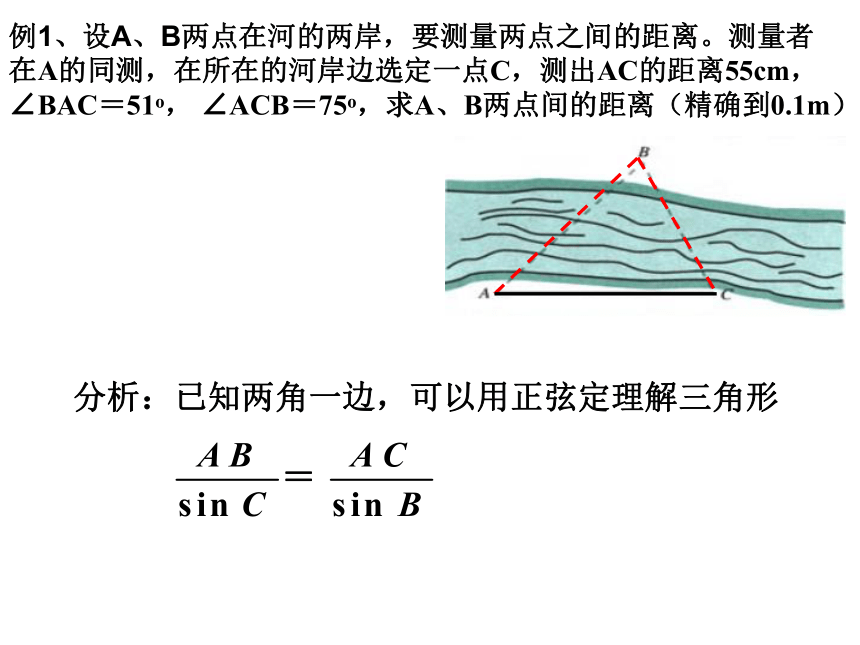
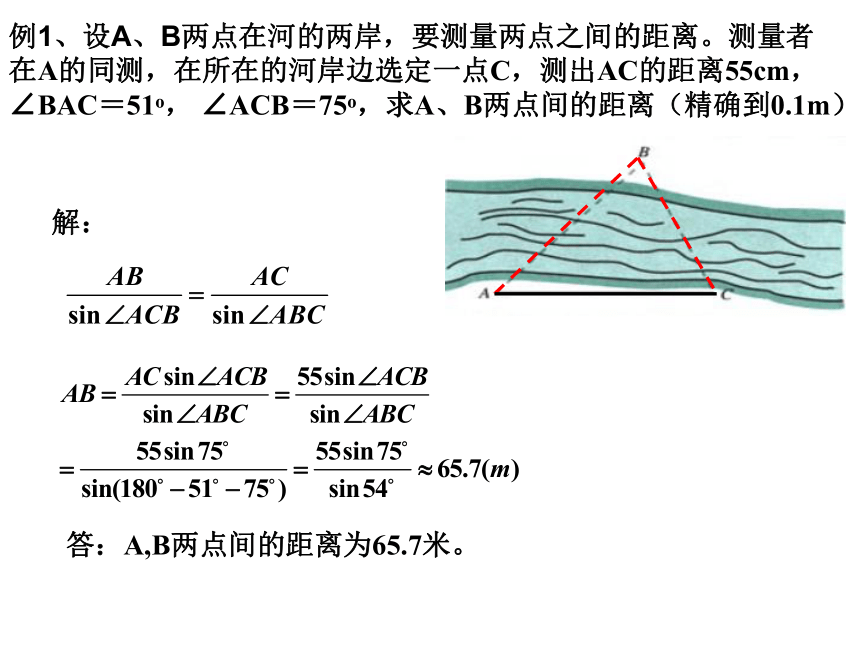
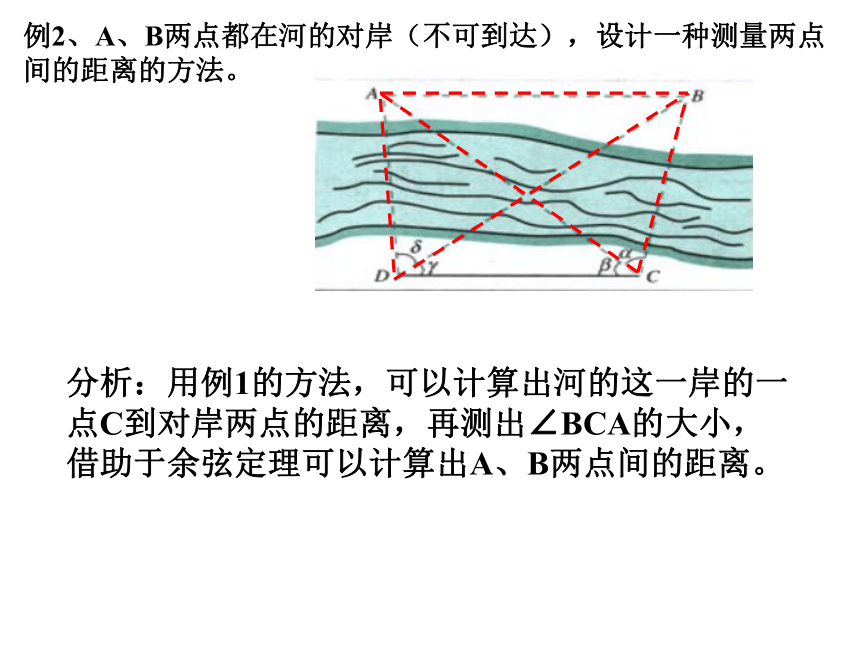
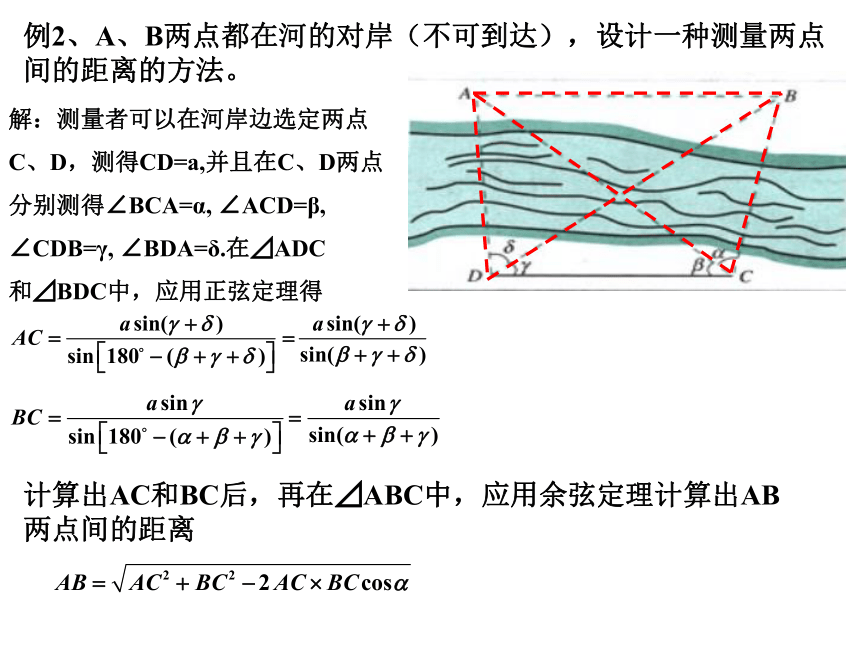
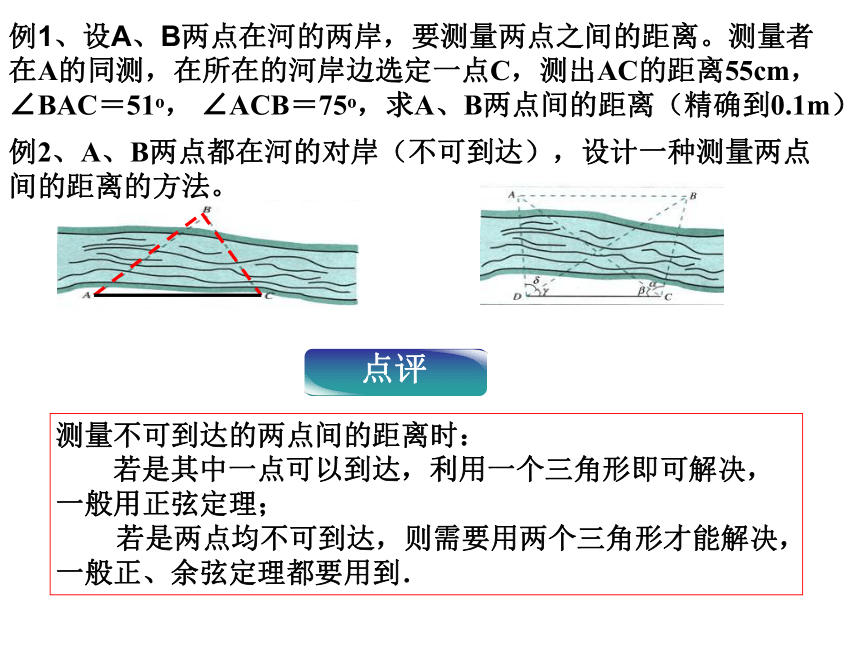
第一课时 正弦定理、余弦定理的应用距离问题高度问题角度问题有关三角形的计算问题正余弦定理在有关距离问题中的应用例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)分析:已知两角一边,可以用正弦定理解三角形例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)答:A,B两点间的距离为65.7米。解:例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。解:测量者可以在河岸边选定两点
C、D,测得CD=a,并且在C、D两点
分别测得∠BCA=α, ∠ACD=β,
∠CDB=γ, ∠BDA=δ.在⊿ADC
和⊿BDC中,应用正弦定理得计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离测量不可到达的两点间的距离时:
若是其中一点可以到达,利用一个三角形即可解决,一般用正弦定理;
若是两点均不可到达,则需要用两个三角形才能解决,一般正、余弦定理都要用到.例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。例3.自动卸货汽车的车厢采用液压机构。设计时需要计算
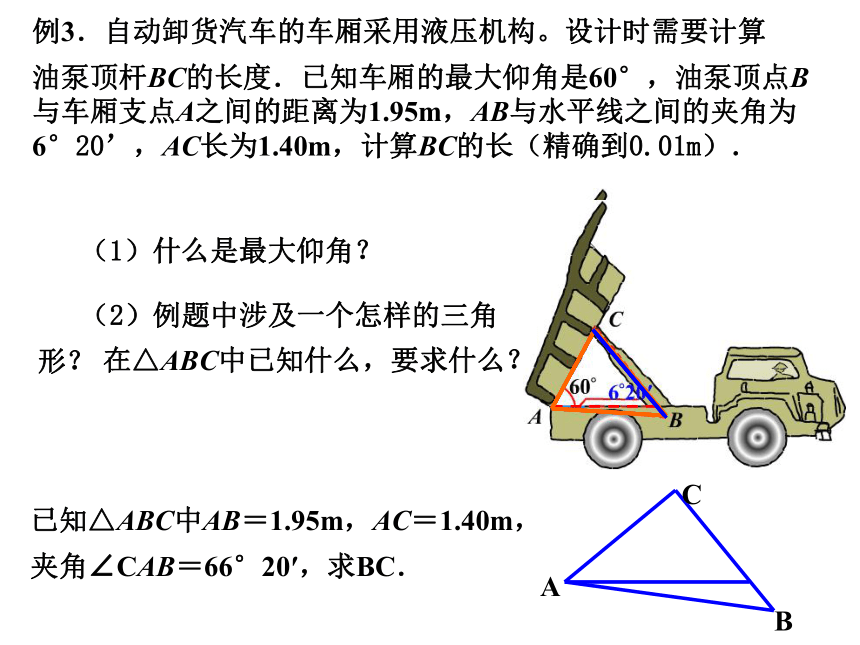
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). (1)什么是最大仰角? (2)例题中涉及一个怎样的三角
形?在△ABC中已知什么,要求什么?已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.例3.自动卸货汽车的车厢采用液压机构。设计时需要计算
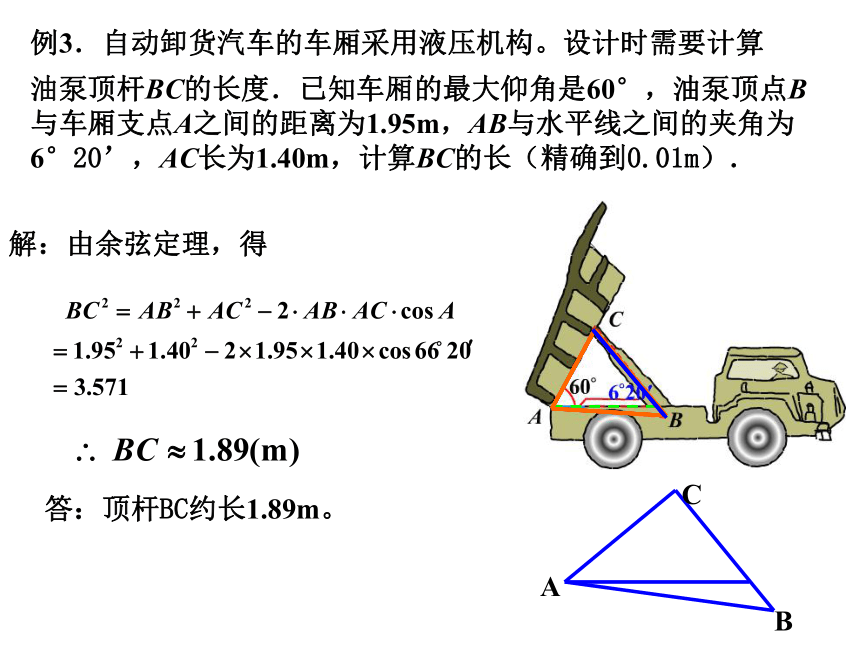
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 解:由余弦定理,得答:顶杆BC约长1.89m。 练习1:如图7所示,隔河可以看见目标A,B,但不能到达,在岸边选择相距 km的C,D两点,并测得∠DCB=45°,∠BDC=75°,∠ADC=30°,∠ACD=120°
(A、B、C、D在同一平面内),求两目标A、B之间的距离.练习2.一货轮在海上由西向东航行,在A处望见灯塔C在货轮的东北方向,半小时后在B处望见灯塔C在货轮的北偏东30°方向.若货轮的速度为30 n mile/h,当货轮航行到D处望见灯塔C在货轮的西北方向时,求A,D两处的距离.课堂小结实际问题 作业:阅读教材12页,理解并掌握基准线定义1.2 解三角形应用举例
第二课时 正弦定理、余弦定理的应用距离问题高度问题角度问题有关三角形的计算问题正余弦定理在有关高度问题中的应用例3 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法分析:由于建筑物的底部B是不可到达的,所以不能直接测量出建筑物的高。由解直角三角形的知识,只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。例3 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在⊿ACD中,根据正弦定理可得例4 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)分析:根据已知条件,应该设法计算出AB或AC的长例4 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,所以,CD=BD-BC≈177-27.3=150(m)答:山的高度约为150米。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。正余弦定理在有关角度问题中的应用例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01n mile)?解:在⊿ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,所以,∠CAB=19.0°,
75°-∠CAB=56.0°.答:此船应该沿北偏东56.0°的方向航行,
需要航行113.15n mile.练习.甲船在A处观察到乙船在它的北偏东60°方向的B处,两船相距a(n mile),乙船向正北方向行驶.若甲船的速度是乙船速度的√3 倍,问甲船应取什么方向前进才能尽快追上乙船?相遇时乙船已行驶多少海里?
1.测量一个底部不能到达的建筑物的高度
解决这类问题的思路是先分别在某水平面和垂直面内构造一个直角三角形,利用正弦定理求出水平三角形的一条直角边长,然后在垂直面内的直角三角形中解出另一直角边(建筑物高)的长.课堂小结2.角的测量
要测量角的大小,可利用测角仪及测距离的钢卷尺等工具结合正弦定理及余弦定理解三角形,实际解决不能直接测得的角的大小的问题.
在解决测量问题的有关题目时,要搞清方位角、俯角与仰角的含义,合理的构造三角形求解,即把实际问题数学化.
1.2 解三角形应用举例
第三课时 正弦定理、余弦定理的应用距离问题高度问题角度问题有关三角形的计算问题正余弦定理在有关三角形的计算问题中的应用[例1] 在△ABC中,BC=5,AC=4,cos∠CAD= 且AD=BD,求△ABC的面积.迁移变式2
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,求AB的长.“边化角”“角化边”提示:可以运用“角化边”,从右向左证明. 解决三角形中计算问题的关键是转化为求三角形中的边或角,再分析所解三角形中已知哪些元素,还需要求出哪些元素.通常情况下,求线段的长转化为求三角形的边长,求角的大小转化为求三角形中角的大小,即放到“形中求”.
第一课时 正弦定理、余弦定理的应用距离问题高度问题角度问题有关三角形的计算问题正余弦定理在有关距离问题中的应用例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)分析:已知两角一边,可以用正弦定理解三角形例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)答:A,B两点间的距离为65.7米。解:例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。解:测量者可以在河岸边选定两点
C、D,测得CD=a,并且在C、D两点
分别测得∠BCA=α, ∠ACD=β,
∠CDB=γ, ∠BDA=δ.在⊿ADC
和⊿BDC中,应用正弦定理得计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离测量不可到达的两点间的距离时:
若是其中一点可以到达,利用一个三角形即可解决,一般用正弦定理;
若是两点均不可到达,则需要用两个三角形才能解决,一般正、余弦定理都要用到.例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离55cm,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。例3.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). (1)什么是最大仰角? (2)例题中涉及一个怎样的三角
形?在△ABC中已知什么,要求什么?已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.例3.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 解:由余弦定理,得答:顶杆BC约长1.89m。 练习1:如图7所示,隔河可以看见目标A,B,但不能到达,在岸边选择相距 km的C,D两点,并测得∠DCB=45°,∠BDC=75°,∠ADC=30°,∠ACD=120°
(A、B、C、D在同一平面内),求两目标A、B之间的距离.练习2.一货轮在海上由西向东航行,在A处望见灯塔C在货轮的东北方向,半小时后在B处望见灯塔C在货轮的北偏东30°方向.若货轮的速度为30 n mile/h,当货轮航行到D处望见灯塔C在货轮的西北方向时,求A,D两处的距离.课堂小结实际问题 作业:阅读教材12页,理解并掌握基准线定义1.2 解三角形应用举例
第二课时 正弦定理、余弦定理的应用距离问题高度问题角度问题有关三角形的计算问题正余弦定理在有关高度问题中的应用例3 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法分析:由于建筑物的底部B是不可到达的,所以不能直接测量出建筑物的高。由解直角三角形的知识,只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。例3 AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在⊿ACD中,根据正弦定理可得例4 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)分析:根据已知条件,应该设法计算出AB或AC的长例4 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,所以,CD=BD-BC≈177-27.3=150(m)答:山的高度约为150米。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。正余弦定理在有关角度问题中的应用例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01n mile)?解:在⊿ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,所以,∠CAB=19.0°,
75°-∠CAB=56.0°.答:此船应该沿北偏东56.0°的方向航行,
需要航行113.15n mile.练习.甲船在A处观察到乙船在它的北偏东60°方向的B处,两船相距a(n mile),乙船向正北方向行驶.若甲船的速度是乙船速度的√3 倍,问甲船应取什么方向前进才能尽快追上乙船?相遇时乙船已行驶多少海里?
1.测量一个底部不能到达的建筑物的高度
解决这类问题的思路是先分别在某水平面和垂直面内构造一个直角三角形,利用正弦定理求出水平三角形的一条直角边长,然后在垂直面内的直角三角形中解出另一直角边(建筑物高)的长.课堂小结2.角的测量
要测量角的大小,可利用测角仪及测距离的钢卷尺等工具结合正弦定理及余弦定理解三角形,实际解决不能直接测得的角的大小的问题.
在解决测量问题的有关题目时,要搞清方位角、俯角与仰角的含义,合理的构造三角形求解,即把实际问题数学化.
1.2 解三角形应用举例
第三课时 正弦定理、余弦定理的应用距离问题高度问题角度问题有关三角形的计算问题正余弦定理在有关三角形的计算问题中的应用[例1] 在△ABC中,BC=5,AC=4,cos∠CAD= 且AD=BD,求△ABC的面积.迁移变式2
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,求AB的长.“边化角”“角化边”提示:可以运用“角化边”,从右向左证明. 解决三角形中计算问题的关键是转化为求三角形中的边或角,再分析所解三角形中已知哪些元素,还需要求出哪些元素.通常情况下,求线段的长转化为求三角形的边长,求角的大小转化为求三角形中角的大小,即放到“形中求”.
