【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修五同步课件:3.1不等关系与不等式(两课时)(共35张PPT)
文档属性
| 名称 | 【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修五同步课件:3.1不等关系与不等式(两课时)(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 414.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-26 18:07:31 | ||
图片预览









文档简介
课件35张PPT。3.1 不等关系与不等式
第一课时横看成岭侧成峰
远近高低各不同日常生活中长短大小轻重高矮数学中,我们用不等式表示不等关系.长短大小轻重高矮1.不等式的定义:用不等号表示不等关系的式子叫不等式。2.初中所学不等式的性质:①不等式的两边都加上(或减去)同一个数或同一个整式,
不等号的方向不变。②不等式的两边都乘以(或除以)同一个正数,不等号的
方向不变。
③不等式的两边都乘以(或除以)同一个负数,不等号的
方向改变。
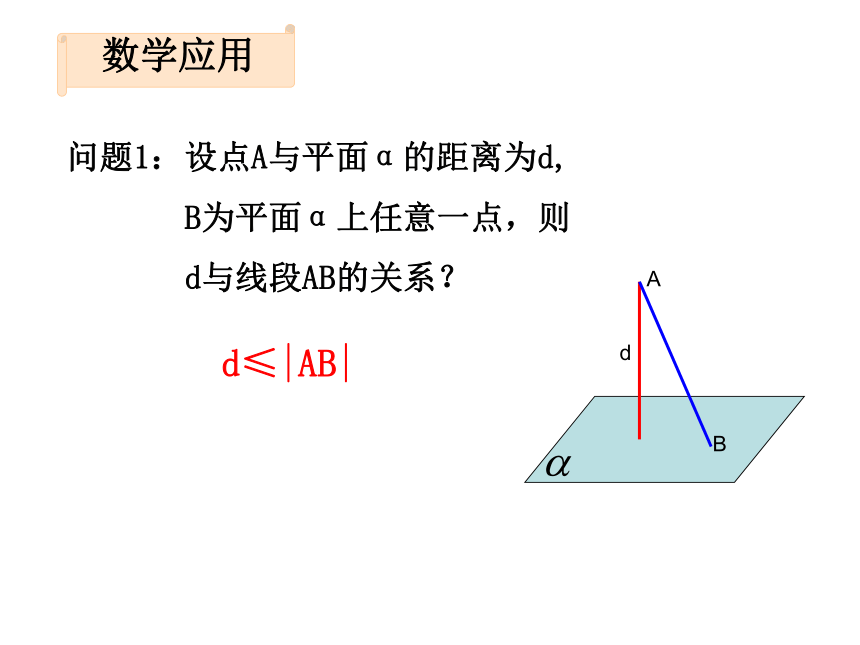
问题1:设点A与平面α的距离为d,
B为平面α上任意一点,则
d与线段AB的关系?
d≤|AB|
数学应用数学应用问题2.某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?分析(1)销售量减少了多少?(2)现在销售量是多少?(3)销售总收入为多少?
用不等式表示为:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
(3)截得两种钢管的数量都不能为负.(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;(1)截得两种钢管的总长度不能超过4000mm;数学应用分析:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
(3)截得两种钢管的数量都不能为负.(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;数学应用分析:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
(3)截得两种钢管的数量都不能为负.数学应用分析:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
数学应用分析:x≥0,y≥0问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式.上面三个不等关系,是“且”的关系,要同时满足的话,用不等式组表示:数学应用分析:x≥0,y≥0考虑到本例的实际意义,还应有x,y∈N问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式.数学应用上面三个不等关系,是“且”的关系,要同时满足的话,用不等式组表示为:x,y∈N1.数轴的三要素:原点、长度单位、正方向2.如何表示数轴上两个点所对数的大小:数轴上右边的点所对的数大于左边的点所对的数。3.A、B是数轴上的两个点,A、B所对的实数分别为a、b,
试比较a-b与0的大小不等式的基本原理 不等式的基本原理解:基本原理的应用基本原理的应用本结论称为
“糖水加糖水更甜原理”<倒数法则:基本原理的应用练习.用不等号填空0____________________≥<<>1.不等关系是普遍存在的2.用不等式(组)来表示不等关系3.不等式基本原理
a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
4.作差比较法
步骤:作差,变形,定号,下结论课堂小结3.1 不等关系与不等式
第二课时复习:不等式的基本原理练习.比较a2+b2+3与2(a-b)的大小。 作差比较大小步骤:
作差—变形—判断—结论 同向不等式: 在两个不等式中,如果每个不等式的左边都大于
(或小于)右边,这两个不等式就是同向不等式。异向不等式: 在两个不等式中,如果一个不等式的左边大于(或
小于)右边,另一个不等式的左边小于(或大于)右边
这两个不等式就是异向不等式。
概念准备证明:由正数的相反数是负数,得即后半部分同学们自己证 不等式的对称性不等式的性质性质2.如果证明:∵两个正数的和仍是正数 ∴ ∴不等式的传递性不等式的性质证明:∵∴从而可得移项法则: 不等式中任何一项改变符号后,可以把它从一边移到
另一边。不等式的可加性不等式的性质性质4. 如果a>b,且c>0,那么ac>bc;
如果a>b,且c<0,那么ac证明:ac-bc=( a-b )c
因为 a >b
所以 a-b>0,
根据同号相乘得正,异号相乘得负,得
当c>0时,(a-b)c>0, 即 ac>bc
当c<0 时,(a-b)c<0, 即 acb>0, c>d>0,则 ac>bd.a1> b1 >0, a2 > b2 > 0,…..,an > bn> 0 a1 a2……an > b1b2……..bn性质7.如果 a>b>0,那么 an > bn > 0
( n∈N,n ≥2 ) a1= a2=….=an > 0 , b1 = b2= ……= bn> 0不等式的同向可乘性不等式的乘方法则不等式的性质 性质8. 如果a>b>0,那么
( n∈N,且 n> 1 )证明:假设则:若 ∴ 不等式的开方法则不等式的性质例证明:例证明二:课堂练习判断下列各式的真假?为什么?
(1) 如果a >b,那么a-c>b-c
(2)如果a > b,那么a/c>b/c
(3)如果ac(4) 如果ac2 > bc2,那么a>b真假假真 课堂小结 不等式的性质思考探究
第一课时横看成岭侧成峰
远近高低各不同日常生活中长短大小轻重高矮数学中,我们用不等式表示不等关系.长短大小轻重高矮1.不等式的定义:用不等号表示不等关系的式子叫不等式。2.初中所学不等式的性质:①不等式的两边都加上(或减去)同一个数或同一个整式,
不等号的方向不变。②不等式的两边都乘以(或除以)同一个正数,不等号的
方向不变。
③不等式的两边都乘以(或除以)同一个负数,不等号的
方向改变。
问题1:设点A与平面α的距离为d,
B为平面α上任意一点,则
d与线段AB的关系?
d≤|AB|
数学应用数学应用问题2.某种杂志原以每本2.5元的价格销售,可以售出8万本。据市场调查,若单价每提高0.1元销售量就可能相应减少2000本。若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?分析(1)销售量减少了多少?(2)现在销售量是多少?(3)销售总收入为多少?
用不等式表示为:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
(3)截得两种钢管的数量都不能为负.(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;(1)截得两种钢管的总长度不能超过4000mm;数学应用分析:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
(3)截得两种钢管的数量都不能为负.(2)截得600mm钢管的数量不能超过500mm
的钢管数量的3倍;数学应用分析:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
(3)截得两种钢管的数量都不能为负.数学应用分析:问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式. 假设截得500mm的钢管x根,截得600mm的钢管y根。
根据题意,应当有什么样的不等式呢?
数学应用分析:x≥0,y≥0问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式.上面三个不等关系,是“且”的关系,要同时满足的话,用不等式组表示:数学应用分析:x≥0,y≥0考虑到本例的实际意义,还应有x,y∈N问题3.某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍, 写出满足上述所有不等关系的不等式.数学应用上面三个不等关系,是“且”的关系,要同时满足的话,用不等式组表示为:x,y∈N1.数轴的三要素:原点、长度单位、正方向2.如何表示数轴上两个点所对数的大小:数轴上右边的点所对的数大于左边的点所对的数。3.A、B是数轴上的两个点,A、B所对的实数分别为a、b,
试比较a-b与0的大小不等式的基本原理 不等式的基本原理解:基本原理的应用基本原理的应用本结论称为
“糖水加糖水更甜原理”<倒数法则:基本原理的应用练习.用不等号填空0____________________≥<<>1.不等关系是普遍存在的2.用不等式(组)来表示不等关系3.不等式基本原理
a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
4.作差比较法
步骤:作差,变形,定号,下结论课堂小结3.1 不等关系与不等式
第二课时复习:不等式的基本原理练习.比较a2+b2+3与2(a-b)的大小。 作差比较大小步骤:
作差—变形—判断—结论 同向不等式: 在两个不等式中,如果每个不等式的左边都大于
(或小于)右边,这两个不等式就是同向不等式。异向不等式: 在两个不等式中,如果一个不等式的左边大于(或
小于)右边,另一个不等式的左边小于(或大于)右边
这两个不等式就是异向不等式。
概念准备证明:由正数的相反数是负数,得即后半部分同学们自己证 不等式的对称性不等式的性质性质2.如果证明:∵两个正数的和仍是正数 ∴ ∴不等式的传递性不等式的性质证明:∵∴从而可得移项法则: 不等式中任何一项改变符号后,可以把它从一边移到
另一边。不等式的可加性不等式的性质性质4. 如果a>b,且c>0,那么ac>bc;
如果a>b,且c<0,那么ac
因为 a >b
所以 a-b>0,
根据同号相乘得正,异号相乘得负,得
当c>0时,(a-b)c>0, 即 ac>bc
当c<0 时,(a-b)c<0, 即 ac
( n∈N,n ≥2 ) a1= a2=….=an > 0 , b1 = b2= ……= bn> 0不等式的同向可乘性不等式的乘方法则不等式的性质 性质8. 如果a>b>0,那么
( n∈N,且 n> 1 )证明:假设则:若 ∴ 不等式的开方法则不等式的性质例证明:例证明二:课堂练习判断下列各式的真假?为什么?
(1) 如果a >b,那么a-c>b-c
(2)如果a > b,那么a/c>b/c
(3)如果ac
