【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修五同步课件:3.2.2补充不等式的解法举例(共15张PPT)
文档属性
| 名称 | 【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修五同步课件:3.2.2补充不等式的解法举例(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-26 18:08:26 | ||
图片预览






文档简介
课件15张PPT。3.2 知识拓充
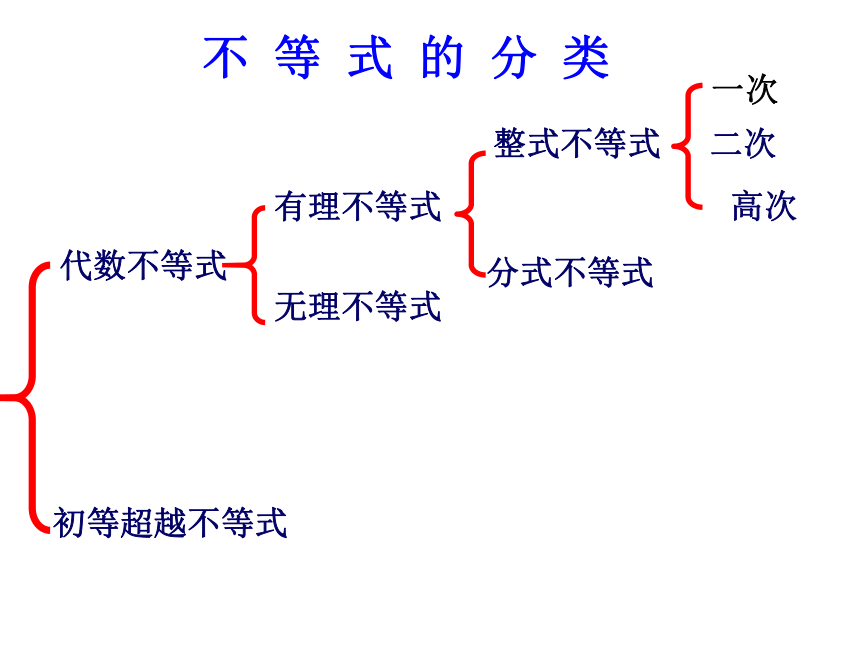
不等式的解法举例不 等 式 的 分 类代数不等式初等超越不等式有理不等式无理不等式整式不等式分式不等式二次高次一次 例1.解不等式解:去分母:12(x+1)+2(x-2)>21x-6去括号:14x+8>21x-6移项、整理:-7x > -14原不等式的解集为{x|x<2}(一) 一元一次不等式(组)的解法例2.解不等式组 10+2x≤11+3x
5x-3 ≤4x-1
7+2x>6+3x解:各不等式的解集分别是
{x|x≥-1},{x|x ≤2},{x|x<1}所以,不等式组的解集是
{x|x≥-1}∩{x|x≤2} ∩{x|x<1}={x|-1≤x<1}(一) 一元一次不等式(组)的解法“三个二次”的关系
一元二次不等式与一元二次方程以及二次函数的图象的关 系有两异根
x1x1=x2=无实根xx2x1 不重不漏的原则2.含有多个绝对值符号的不等式步骤:
1.找零点
2.划区间,并对每个区间解不等式。
3.合并得不等式的解。(三) 含有绝对值的不等式(组)的解法例2、解不等式:x(x-1)(x-2)2(x2-1)(x3-1)>0解:将不等式化为 x(x-1)3(x-2)2(x+1)(x2+x+1)>0∵ x2+x+1>0∴不等式等价于x(x-1)3(x-2)2(x+1)>0∴不等式的解集为{x|-11且x≠2.}两个强调:
1.每个因式中,变量的最高次幂为正
2.遵循“奇过偶不过”原则012-1(四)高次不等式的解法根轴法要注意“点实点虚”根轴法(数轴曲线法)(五)分式不等式的解法1.转化为整式型不等式(组)
等价变形如下 :例1.解不等式解法一:这个不等式的解集是下面的不等式组 (1) 及不等式组(2)的解集的并集: x2-3x+2>0 ①
x2-2x-3<0 ②x2-3x+2<0 ③
x2-2x-3>0 ④(1)(2)不等式①的解集为 {x|x<1或x>2},不等式②的解集为{x|-1 {x|-13},因此不等式组(2)的解集为?.由此可知,原不等式的解集为{x|-1 利用根轴法(数轴曲线法)解法二:原不等式(六)指数、对数不等式的解法【方法指导】
关键先“统一形式”,再利用函数自身及其性质不等式(1)为原不等式的解集是原不等式的解集是(七)含参不等式的解法“分类讨论”小结:常见不等式的解法(一) 一元一次不等式(组)的解法(二) 一元二次不等式(组)的解法
利用“三个二次”的关系(三) 含有绝对值的不等式(组)的解法
多个绝对值符号的“零点讨论法”(四) 高次不等式的解法 “根轴法”(五) 分式不等式的解法
讨论符号,或转化为整式不等式.(六) 指数、对数不等式的解法 关键“统一形式”(七) 含参不等式的解法 “分类讨论”x2-4x+ 4
x2-7x+12
解下列不等式
1. ≥0.
2. x2(x-3)3(x+1)2(x-2)<0.练习
不等式的解法举例不 等 式 的 分 类代数不等式初等超越不等式有理不等式无理不等式整式不等式分式不等式二次高次一次 例1.解不等式解:去分母:12(x+1)+2(x-2)>21x-6去括号:14x+8>21x-6移项、整理:-7x > -14原不等式的解集为{x|x<2}(一) 一元一次不等式(组)的解法例2.解不等式组 10+2x≤11+3x
5x-3 ≤4x-1
7+2x>6+3x解:各不等式的解集分别是
{x|x≥-1},{x|x ≤2},{x|x<1}所以,不等式组的解集是
{x|x≥-1}∩{x|x≤2} ∩{x|x<1}={x|-1≤x<1}(一) 一元一次不等式(组)的解法“三个二次”的关系
一元二次不等式与一元二次方程以及二次函数的图象的关 系有两异根
x1
1.找零点
2.划区间,并对每个区间解不等式。
3.合并得不等式的解。(三) 含有绝对值的不等式(组)的解法例2、解不等式:x(x-1)(x-2)2(x2-1)(x3-1)>0解:将不等式化为 x(x-1)3(x-2)2(x+1)(x2+x+1)>0∵ x2+x+1>0∴不等式等价于x(x-1)3(x-2)2(x+1)>0∴不等式的解集为{x|-1
1.每个因式中,变量的最高次幂为正
2.遵循“奇过偶不过”原则012-1(四)高次不等式的解法根轴法要注意“点实点虚”根轴法(数轴曲线法)(五)分式不等式的解法1.转化为整式型不等式(组)
等价变形如下 :例1.解不等式解法一:这个不等式的解集是下面的不等式组 (1) 及不等式组(2)的解集的并集: x2-3x+2>0 ①
x2-2x-3<0 ②x2-3x+2<0 ③
x2-2x-3>0 ④(1)(2)不等式①的解集为 {x|x<1或x>2},不等式②的解集为{x|-1
关键先“统一形式”,再利用函数自身及其性质不等式(1)为原不等式的解集是原不等式的解集是(七)含参不等式的解法“分类讨论”小结:常见不等式的解法(一) 一元一次不等式(组)的解法(二) 一元二次不等式(组)的解法
利用“三个二次”的关系(三) 含有绝对值的不等式(组)的解法
多个绝对值符号的“零点讨论法”(四) 高次不等式的解法 “根轴法”(五) 分式不等式的解法
讨论符号,或转化为整式不等式.(六) 指数、对数不等式的解法 关键“统一形式”(七) 含参不等式的解法 “分类讨论”x2-4x+ 4
x2-7x+12
解下列不等式
1. ≥0.
2. x2(x-3)3(x+1)2(x-2)<0.练习
