3.9 弧长及扇形面积 同步练习(含详解) 2024-2025学年九年级数学北师大版下册
文档属性
| 名称 | 3.9 弧长及扇形面积 同步练习(含详解) 2024-2025学年九年级数学北师大版下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 20:13:07 | ||
图片预览


文档简介
3.9弧长及扇形面积 同步练习
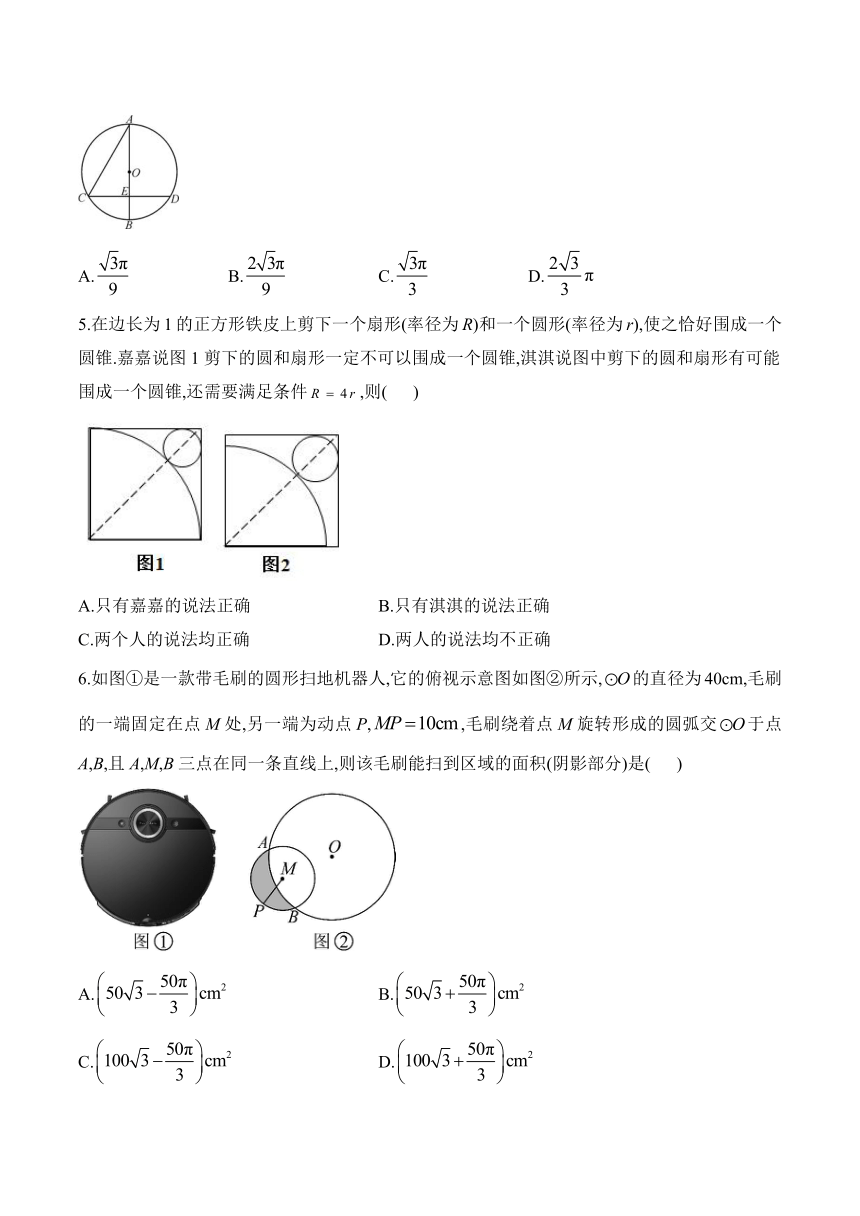
1.如图,已知的半径为6,,是的弦,若,则弧的长是( )
A. B. C. D.
2.如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若,,则阴影部分的面积为( )
A. B. C. D.
3.如图,AB是的直径,点C是上一点,点D在BA的延长线上,CD与交于另一点E,,,则弧BC的长度为( )
A. B. C. D.
4.如图,以AB为直径的与弦CD相交于点E,且,,,则弧BD的长是( )
A. B. C. D.
5.在边长为1的正方形铁皮上剪下一个扇形(率径为R)和一个圆形(率径为r),使之恰好围成一个圆锥.嘉嘉说图1剪下的圆和扇形一定不可以围成一个圆锥,淇淇说图中剪下的圆和扇形有可能围成一个圆锥,还需要满足条件,则( )
A.只有嘉嘉的说法正确 B.只有淇淇的说法正确
C.两个人的说法均正确 D.两人的说法均不正确
6.如图①是一款带毛刷的圆形扫地机器人,它的俯视示意图如图②所示,的直径为40cm,毛刷的一端固定在点M处,另一端为动点P,,毛刷绕着点M旋转形成的圆弧交于点A,B,且A,M,B三点在同一条直线上,则该毛刷能扫到区域的面积(阴影部分)是( )
A. B.
C. D.
7.如图,四边形是边长为的正方形,曲线是由多段的圆心角所对的弧组成的,的圆心为A,半径为,的圆心为B,半径为,的圆心为C,半径为,的圆心为D,半径为,…,,,,的圆心依次为A、B、C、D循环,则弧的长是( )
A. B. C. D.
8.如图,在平行四边形中,点A,B,C在上,连接,若,则图中阴影部分的面积为( )
A. B. C. D.
9.如图,菱形中,分别以点B,D为圆心,以长为半径画弧,分别交边,于点E,F.若,,则图中阴影部分的面积为______.(结果保留)
10.如图,正八边形ABCDEFGH的边长为3,以顶点A为圆心,AB的长为半径画圆,则阴影部分的面积为_______(结果保留π)
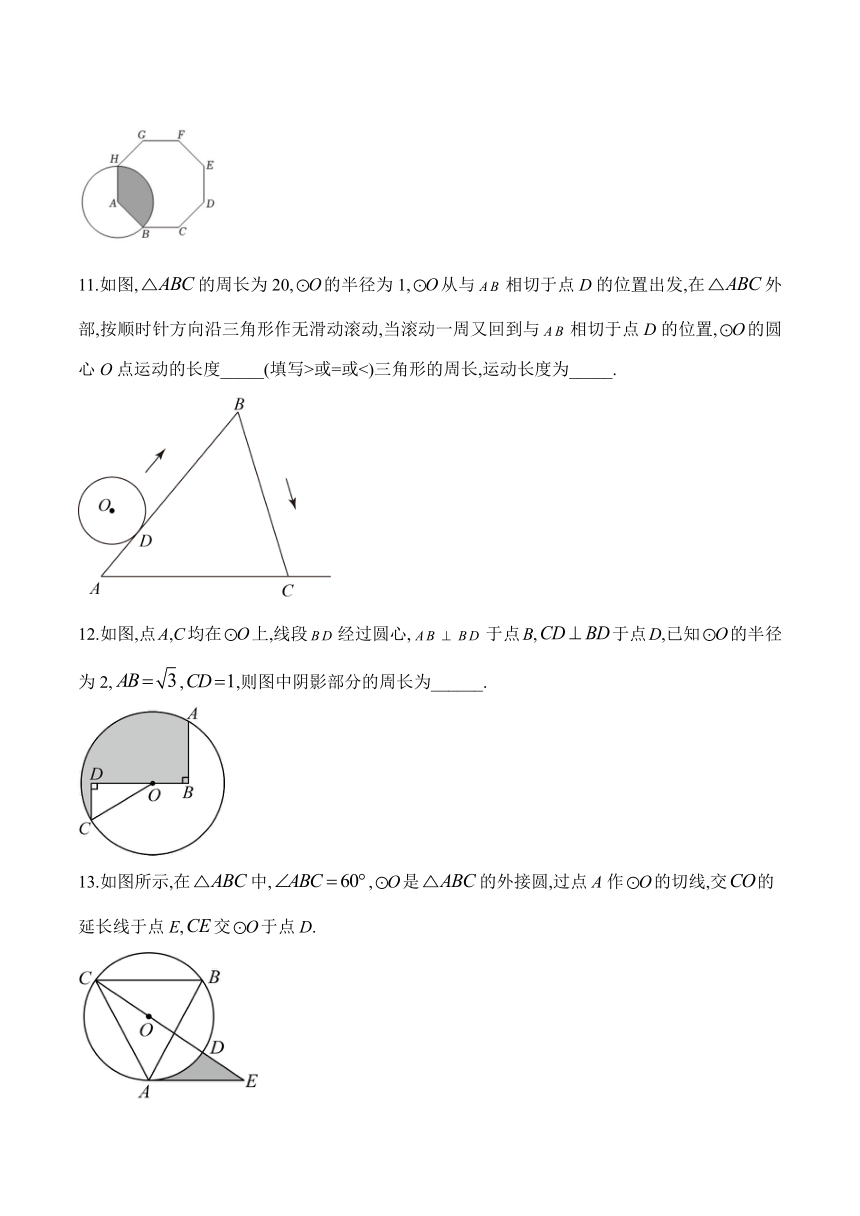
11.如图,的周长为20,的半径为1,从与相切于点D的位置出发,在外部,按顺时针方向沿三角形作无滑动滚动,当滚动一周又回到与相切于点D的位置,的圆心O点运动的长度_____(填写>或=或<)三角形的周长,运动长度为_____.
12.如图,点A,C均在上,线段经过圆心,于点B,于点D,已知的半径为2,,,则图中阴影部分的周长为______.
13.如图所示,在中,,是的外接圆,过点A作的切线,交的延长线于点E,交于点D.
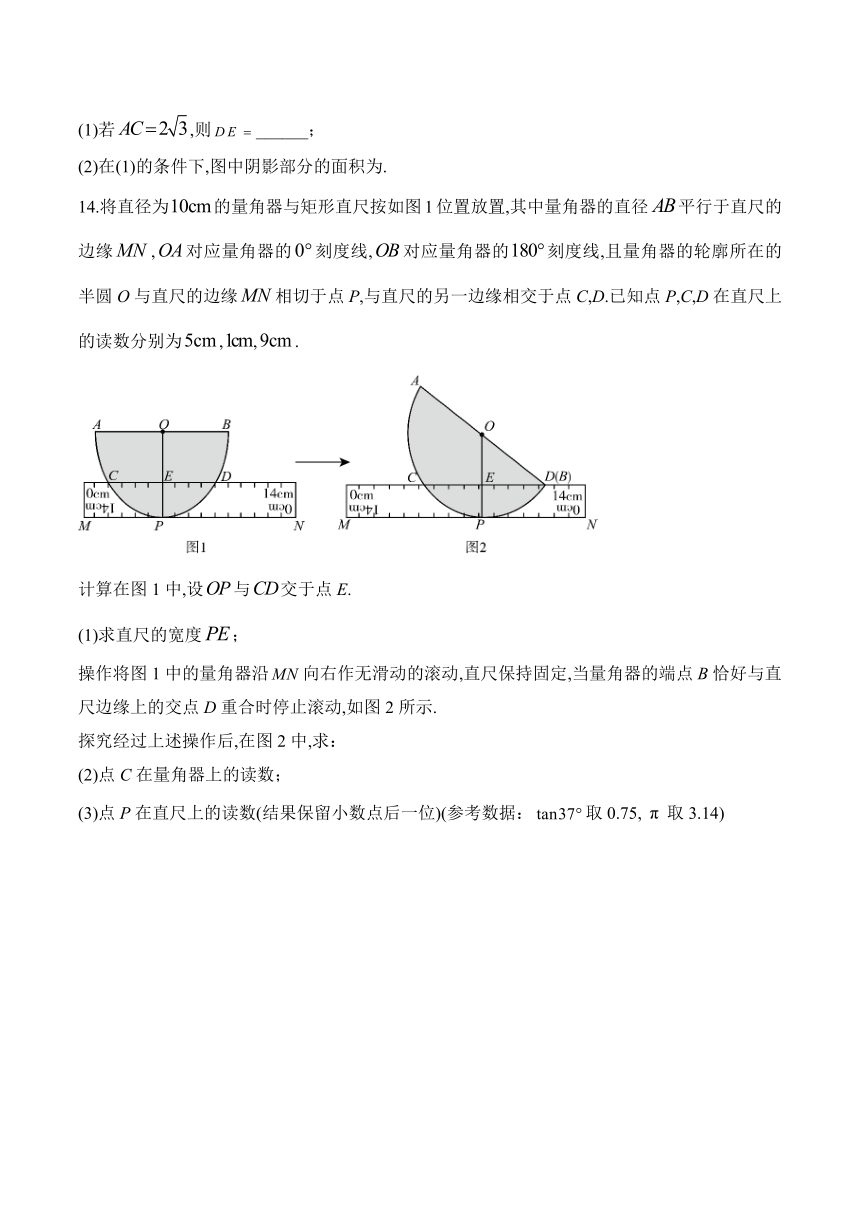
(1)若,则______;
(2)在(1)的条件下,图中阴影部分的面积为.
14.将直径为的量角器与矩形直尺按如图1位置放置,其中量角器的直径平行于直尺的边缘,对应量角器的刻度线,对应量角器的刻度线,且量角器的轮廓所在的半圆O与直尺的边缘相切于点P,与直尺的另一边缘相交于点C,D.已知点P,C,D在直尺上的读数分别为,,.
计算在图1中,设与交于点E.
(1)求直尺的宽度;
操作将图1中的量角器沿向右作无滑动的滚动,直尺保持固定,当量角器的端点B恰好与直尺边缘上的交点D重合时停止滚动,如图2所示.
探究经过上述操作后,在图2中,求:
(2)点C在量角器上的读数;
(3)点P在直尺上的读数(结果保留小数点后一位)(参考数据:取0.75,取3.14)
答案以及解析
1.答案:C
解析:如图,连接OA,OC,
,
弧AC的长为:,
故选:C.
2.答案:D
解析:连接,
四边形是矩形,
,
中,,,
,,
,
.
故选:D.
3.答案:A
解析:连接OE、OC,如图,
∵,
∴,
∴,
∵,
∴,
∴,
∴的长度,
故选A.
4.答案:B
解析:连接OC.
∵中,,,,∴,∴是直角三角形,即AE⊥CD.
∵,∴,∴,∴,即,解得:.
∵,∴,∴.
故选B.
5.答案:C
解析:由题图(1),知正方形的边长为R,
正方形的对角线,
.
,,
要使剪下的圆和扇形可以围成一个圆锥,则扇形的弧长等于底面圆(小圆)的周长
,,
将代人,得
题图(1)剪下的圆利扇形一定不可以围成一个圆锥,瞢諪说的对.
题图(2)中当时,
,淇淇说的对.
故选C.
6.答案:C
解析:如图,连接,,,由题意可知点M是点A,P,B所在圆的圆心.
∵A,M,B三点在同一条直线上,
∴是的直径,
∴.
∵的直径为40cm,
∴,
∵,
∴,
∴是等边三角形,
∴.
∴,
∴,
∴.
故选:C.
7.答案:A
解析:四边形是边长为的正方形,
,
,
弧所对的半径为1,
,
弧所对的半径为,
同理可知:弧的所对的半径为2,弧的所对的半径为,
曲线是由一段度的弧组成的,半径每次比前一段弧半径加,
弧的半径为3,弧的半径为5,弧的半径为7,
弧的半径为,
弧的半径为,
弧的长为,
故选A.
8.答案:B
解析:连接,与交于点D,如图:
∵点A,B,C在上,
,
∵在平行四边形中,,
∴四边形为菱形,
又∵,
,,即为等边三角形,
,
同理,
∴,
,
∴,
在中,,
,
,,
,
故选:B.
9.答案:
解析:如图,连接AC交BD于点O,则
四边形ABCD是菱形,,
,,
在中,,,
,,
,
故答案为:.
10.答案:;
解析:由题意得,,
故答案为:.
11.答案:>;/
解析:如图,四边形、四边形、四边形都是矩形,
根据题意可知,的圆心O的运动的总长度为线段、、及、、的长度的和,
∵,,,
∴的圆心O点运动的长度大于的周长,
∵,
∴,
∴、、的长度和等于一个半径长为1的圆的周长,即,
∵,
∴圆心O点运动长度为,
故答案为:>,.
12.答案:
解析:∵于点B,于点D,
∴,,
∵的半径为2,
∴,
∵,,
∴,,
∴,,
∴,,
∴,
∴的长度为:,
∴图中阴影部分的周长为;
故答案为:.
13.答案:2;
解析:如图,连接AD、OA,
是的直径,
由圆周角定理得,
,
在中,,
,
即,
解得,
是的切线,
由圆周角定理得,
,
,
故答案为:2;
(2)在中,
阴影部分的面积
故答案为:.
14.答案:(1)
(2)
(3)
解析:(1)∵C,D在直尺上的读数分别为,,
∴,
∵半圆O与相切于点P,
∴,
又∵,
∴,
∴,
连接,在中,,
,
∴;
(2)连接,在中,,
∴,
∴,
即点C在量角器上的读数为;
(3)取半圆弧的中点为Q,连接,
∴,
∴,
∴,
即经操作后,点P移动的距离为,
∴点P在直尺上的读数为.
1.如图,已知的半径为6,,是的弦,若,则弧的长是( )
A. B. C. D.
2.如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若,,则阴影部分的面积为( )
A. B. C. D.
3.如图,AB是的直径,点C是上一点,点D在BA的延长线上,CD与交于另一点E,,,则弧BC的长度为( )
A. B. C. D.
4.如图,以AB为直径的与弦CD相交于点E,且,,,则弧BD的长是( )
A. B. C. D.
5.在边长为1的正方形铁皮上剪下一个扇形(率径为R)和一个圆形(率径为r),使之恰好围成一个圆锥.嘉嘉说图1剪下的圆和扇形一定不可以围成一个圆锥,淇淇说图中剪下的圆和扇形有可能围成一个圆锥,还需要满足条件,则( )
A.只有嘉嘉的说法正确 B.只有淇淇的说法正确
C.两个人的说法均正确 D.两人的说法均不正确
6.如图①是一款带毛刷的圆形扫地机器人,它的俯视示意图如图②所示,的直径为40cm,毛刷的一端固定在点M处,另一端为动点P,,毛刷绕着点M旋转形成的圆弧交于点A,B,且A,M,B三点在同一条直线上,则该毛刷能扫到区域的面积(阴影部分)是( )
A. B.
C. D.
7.如图,四边形是边长为的正方形,曲线是由多段的圆心角所对的弧组成的,的圆心为A,半径为,的圆心为B,半径为,的圆心为C,半径为,的圆心为D,半径为,…,,,,的圆心依次为A、B、C、D循环,则弧的长是( )
A. B. C. D.
8.如图,在平行四边形中,点A,B,C在上,连接,若,则图中阴影部分的面积为( )
A. B. C. D.
9.如图,菱形中,分别以点B,D为圆心,以长为半径画弧,分别交边,于点E,F.若,,则图中阴影部分的面积为______.(结果保留)
10.如图,正八边形ABCDEFGH的边长为3,以顶点A为圆心,AB的长为半径画圆,则阴影部分的面积为_______(结果保留π)
11.如图,的周长为20,的半径为1,从与相切于点D的位置出发,在外部,按顺时针方向沿三角形作无滑动滚动,当滚动一周又回到与相切于点D的位置,的圆心O点运动的长度_____(填写>或=或<)三角形的周长,运动长度为_____.
12.如图,点A,C均在上,线段经过圆心,于点B,于点D,已知的半径为2,,,则图中阴影部分的周长为______.
13.如图所示,在中,,是的外接圆,过点A作的切线,交的延长线于点E,交于点D.
(1)若,则______;
(2)在(1)的条件下,图中阴影部分的面积为.
14.将直径为的量角器与矩形直尺按如图1位置放置,其中量角器的直径平行于直尺的边缘,对应量角器的刻度线,对应量角器的刻度线,且量角器的轮廓所在的半圆O与直尺的边缘相切于点P,与直尺的另一边缘相交于点C,D.已知点P,C,D在直尺上的读数分别为,,.
计算在图1中,设与交于点E.
(1)求直尺的宽度;
操作将图1中的量角器沿向右作无滑动的滚动,直尺保持固定,当量角器的端点B恰好与直尺边缘上的交点D重合时停止滚动,如图2所示.
探究经过上述操作后,在图2中,求:
(2)点C在量角器上的读数;
(3)点P在直尺上的读数(结果保留小数点后一位)(参考数据:取0.75,取3.14)
答案以及解析
1.答案:C
解析:如图,连接OA,OC,
,
弧AC的长为:,
故选:C.
2.答案:D
解析:连接,
四边形是矩形,
,
中,,,
,,
,
.
故选:D.
3.答案:A
解析:连接OE、OC,如图,
∵,
∴,
∴,
∵,
∴,
∴,
∴的长度,
故选A.
4.答案:B
解析:连接OC.
∵中,,,,∴,∴是直角三角形,即AE⊥CD.
∵,∴,∴,∴,即,解得:.
∵,∴,∴.
故选B.
5.答案:C
解析:由题图(1),知正方形的边长为R,
正方形的对角线,
.
,,
要使剪下的圆和扇形可以围成一个圆锥,则扇形的弧长等于底面圆(小圆)的周长
,,
将代人,得
题图(1)剪下的圆利扇形一定不可以围成一个圆锥,瞢諪说的对.
题图(2)中当时,
,淇淇说的对.
故选C.
6.答案:C
解析:如图,连接,,,由题意可知点M是点A,P,B所在圆的圆心.
∵A,M,B三点在同一条直线上,
∴是的直径,
∴.
∵的直径为40cm,
∴,
∵,
∴,
∴是等边三角形,
∴.
∴,
∴,
∴.
故选:C.
7.答案:A
解析:四边形是边长为的正方形,
,
,
弧所对的半径为1,
,
弧所对的半径为,
同理可知:弧的所对的半径为2,弧的所对的半径为,
曲线是由一段度的弧组成的,半径每次比前一段弧半径加,
弧的半径为3,弧的半径为5,弧的半径为7,
弧的半径为,
弧的半径为,
弧的长为,
故选A.
8.答案:B
解析:连接,与交于点D,如图:
∵点A,B,C在上,
,
∵在平行四边形中,,
∴四边形为菱形,
又∵,
,,即为等边三角形,
,
同理,
∴,
,
∴,
在中,,
,
,,
,
故选:B.
9.答案:
解析:如图,连接AC交BD于点O,则
四边形ABCD是菱形,,
,,
在中,,,
,,
,
故答案为:.
10.答案:;
解析:由题意得,,
故答案为:.
11.答案:>;/
解析:如图,四边形、四边形、四边形都是矩形,
根据题意可知,的圆心O的运动的总长度为线段、、及、、的长度的和,
∵,,,
∴的圆心O点运动的长度大于的周长,
∵,
∴,
∴、、的长度和等于一个半径长为1的圆的周长,即,
∵,
∴圆心O点运动长度为,
故答案为:>,.
12.答案:
解析:∵于点B,于点D,
∴,,
∵的半径为2,
∴,
∵,,
∴,,
∴,,
∴,,
∴,
∴的长度为:,
∴图中阴影部分的周长为;
故答案为:.
13.答案:2;
解析:如图,连接AD、OA,
是的直径,
由圆周角定理得,
,
在中,,
,
即,
解得,
是的切线,
由圆周角定理得,
,
,
故答案为:2;
(2)在中,
阴影部分的面积
故答案为:.
14.答案:(1)
(2)
(3)
解析:(1)∵C,D在直尺上的读数分别为,,
∴,
∵半圆O与相切于点P,
∴,
又∵,
∴,
∴,
连接,在中,,
,
∴;
(2)连接,在中,,
∴,
∴,
即点C在量角器上的读数为;
(3)取半圆弧的中点为Q,连接,
∴,
∴,
∴,
即经操作后,点P移动的距离为,
∴点P在直尺上的读数为.
