3.8圆内接正多边形 同步练习 (含详解) 2024-2025学年九年级数学北师大版下册
文档属性
| 名称 | 3.8圆内接正多边形 同步练习 (含详解) 2024-2025学年九年级数学北师大版下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 931.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 00:00:00 | ||
图片预览


文档简介
3.8圆内接正多边形 同步练习
1.如图,正五边形ABCDE内接于点F为的中点,直线AP与相切于点A,则的度数是( )
A.36° B.54° C.60° D.72°
2.早在1800多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积,如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为( )
A.3 B. C. D.6
3.如图,多边形是的内接正n边形,已知的半径为r,的度数为,点O到的距离为d,的面积为S.下面三个推断中.
①当n变化时,随n的变化而变化,与n满足的函数关系是反比例函数关系;
②若为定值,当r变化时,d随r的变化而变化,d与r满足的函数关系是正比例函数关系;
③若n为定值,当r变化时,S随r的变化而变化,S与r满足的函数关系是二次函数关系.
其中正确的是( )
A.①② B.①③ C.②③ D.①②③
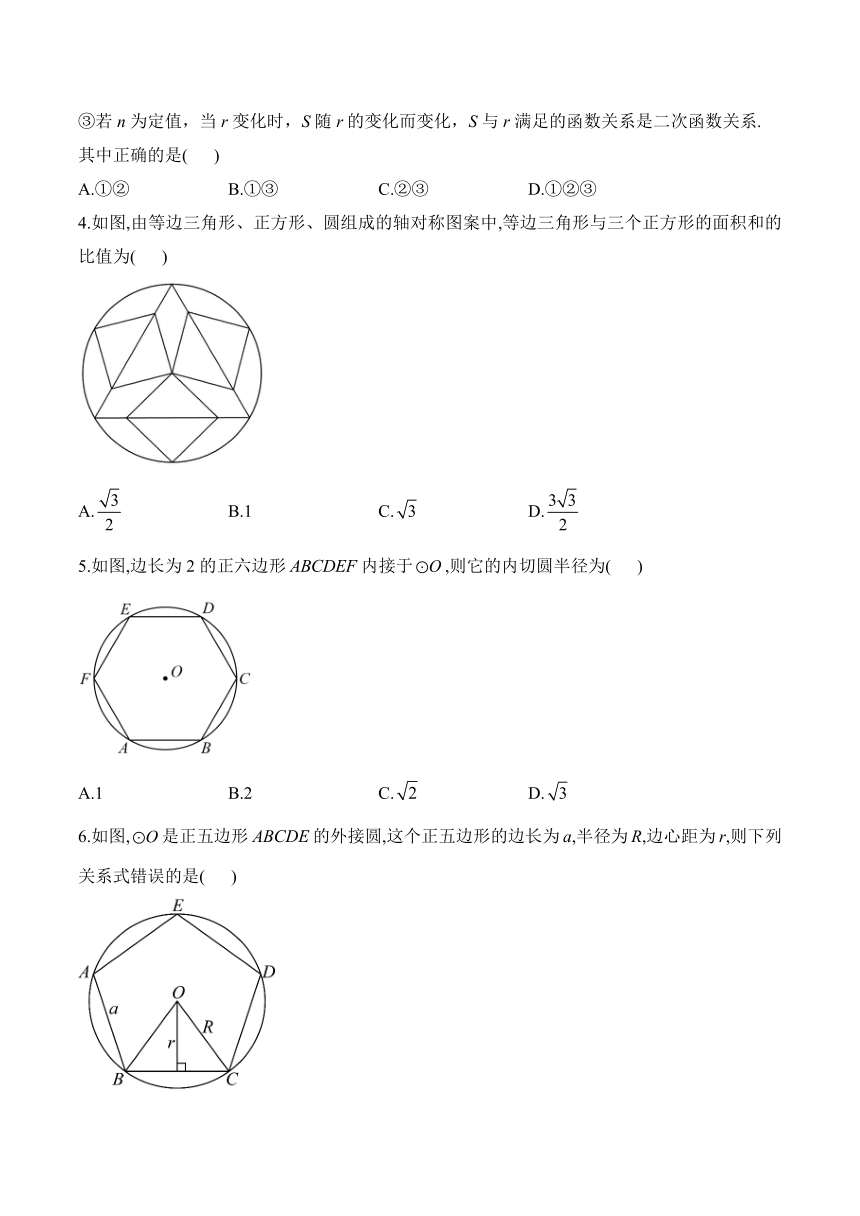
4.如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与三个正方形的面积和的比值为( )
A. B.1 C. D.
5.如图,边长为2的正六边形内接于,则它的内切圆半径为( )
A.1 B.2 C. D.
6.如图,是正五边形的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A. B. C. D.
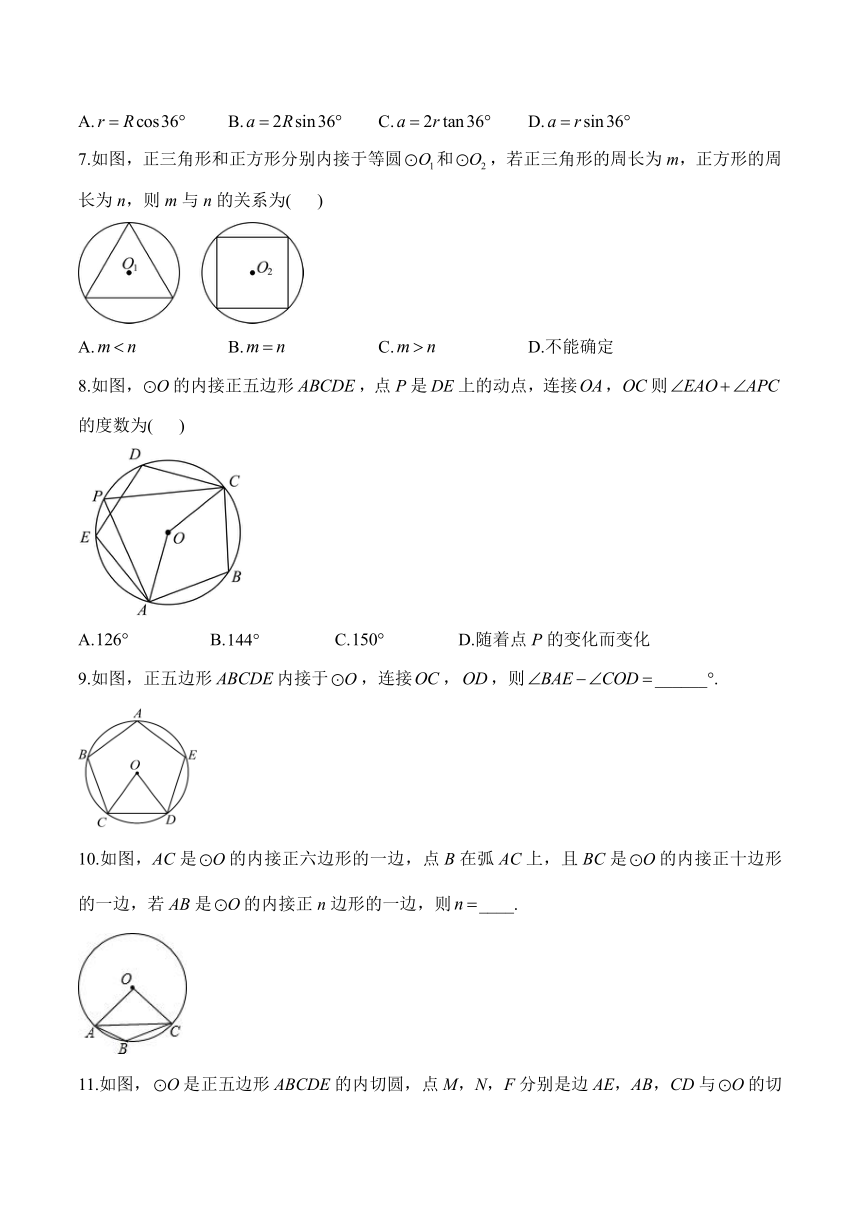
7.如图,正三角形和正方形分别内接于等圆和,若正三角形的周长为m,正方形的周长为n,则m与n的关系为( )
A. B. C. D.不能确定
8.如图,的内接正五边形,点P是上的动点,连接,则的度数为( )
A. B. C. D.随着点P的变化而变化
9.如图,正五边形内接于,连接,,则______°.
10.如图,AC是的内接正六边形的一边,点B在弧AC上,且BC是的内接正十边形的一边,若AB是的内接正n边形的一边,则____.
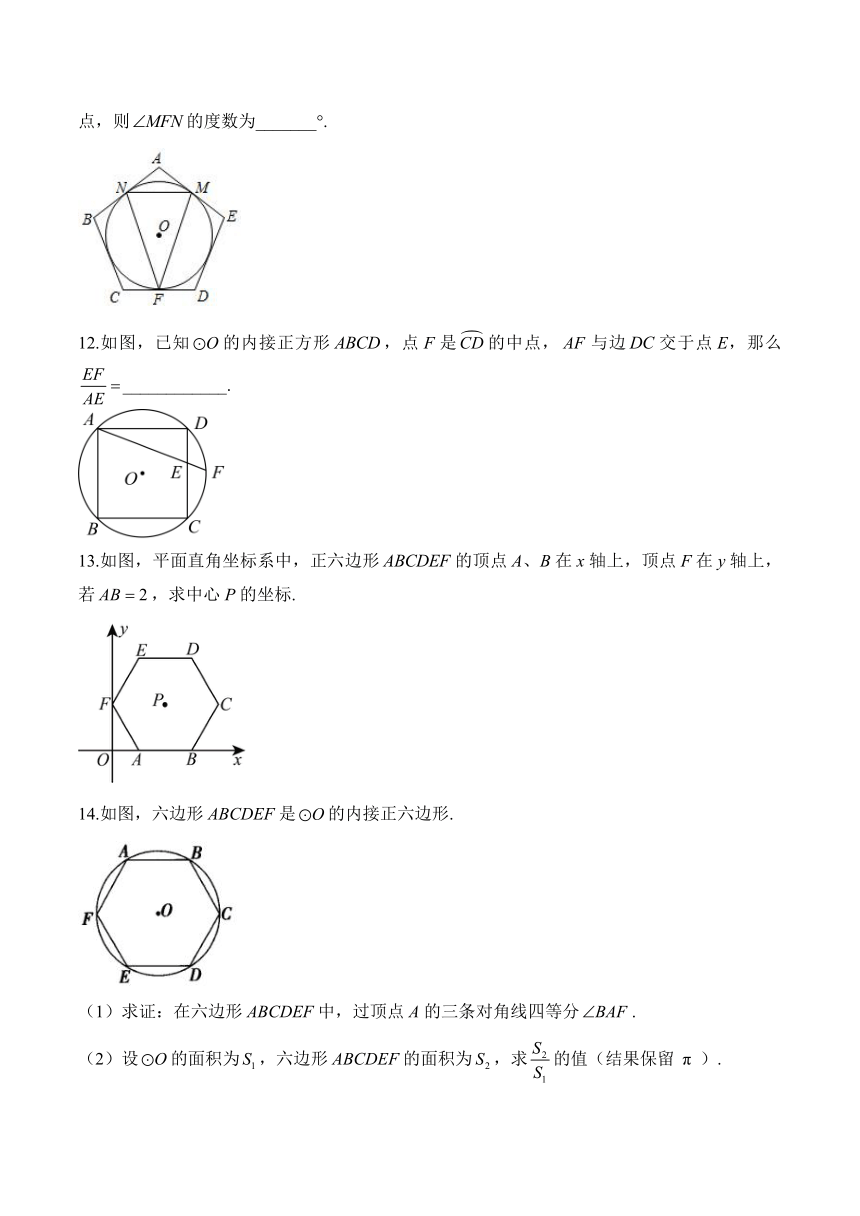
11.如图,是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与的切点,则的度数为_______°.
12.如图,已知的内接正方形,点F是的中点,与边交于点E,那么____________.
13.如图,平面直角坐标系中,正六边形的顶点A、B在x轴上,顶点F在y轴上,若,求中心P的坐标.
14.如图,六边形ABCDEF是的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分.
(2)设的面积为,六边形ABCDEF的面积为,求的值(结果保留).
答案以及解析
1.答案:B
解析:连接EF,
正五边形ABCDE内接于O点F为BC的中点,
所对的圆心角为,
,
直线AP与O相切于点A,
故选B.
2.答案:A
解析:如图,过A作于C,
∵圆的内接正十二边形的圆心角为,,
∴,
∴,
∴这个圆的内接正十二边形的面积为,
故选:A.
3.答案:D
解析:①,所以与n满足的函数关系是反比例函数关系,正确;
②,所以,所以d与r满足的函数关系是正比例函数关系,正确;
③,所以S与r满足的函数关系是二次函数关系,正确.
故选D.
4.答案:A
解析:如图,设圆的圆心为O,过A作于于D,则AD必过点O,且;
的边长为,则,,,
∴正方形的边长为,面积为,三个正方形的面积和为,
的面积为,
∴等边三角形与三个正方形的面积和的比值为.
故选A.
5.答案:D
解析:如图,连接,,作于G,
∵,,
∴是等边三角形,
∴,
∵,
∴,
∴,
即它的内切圆半径为,
故选:D.
6.答案:D
解析:是正五边形的外接圆,
,
∵,,
,,
∴,即,故B不符合题意;D符合题意;
,即,故C不符合题意;
,即,故A不符合题意;
故选:D.
7.答案:A
解析:设等圆和的半径为r,如图,,
正三角形和正方形分别内接于等圆和,
∴,,
,,,
,,
,
,
,
;
故选A.
8.答案:A
解析:连接,
是的内接正五边形,
,,
,,
,
,
在与中,
,
,
,
,
,
故选:A.
9.答案:
解析:∵五边形是正五边形,
∴,,
∴,
故答案为:.
10.答案:15
解析:连接OB,是的内接正六边形的一边,
,
是的内接正十边形的一边,
,
,
即,,
故答案为15.
11.答案:36
解析:如图,连接OM,ON.
M,N,F分别是AE,AB,CD与的切点,
,,
,
,
,
,
故答案为:36.
12.答案:
解析:如图所示,连接,交于点G,连接,
的内接正方形,
经过点O,
点F是的中点,
,
设,则
,
,
,
故答案为:.
13.答案:
解析:连接、,过点P作轴于Q,
六边形是正六边形,,
,,,,
,是等边三角形,,
,,,
,
,
中心P的坐标为.
14.答案:(1)证明见解析
(2)
解析:(1)证明:如图,连接AE,AD,AC,
六边形ABCDEF是的内接正六边形,
,
,
,
过顶点A的三条对角线四等分.
(2)如图,过点O作于点G,连接OE.
设的半径为R,
,,
是边长为R的等边三角形,
六边形ABCDEF的周长.
在中,,,
利用勾股定理得,
正六边形ABCDEF的面积.
的面积,
.
1.如图,正五边形ABCDE内接于点F为的中点,直线AP与相切于点A,则的度数是( )
A.36° B.54° C.60° D.72°
2.早在1800多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积,如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为( )
A.3 B. C. D.6
3.如图,多边形是的内接正n边形,已知的半径为r,的度数为,点O到的距离为d,的面积为S.下面三个推断中.
①当n变化时,随n的变化而变化,与n满足的函数关系是反比例函数关系;
②若为定值,当r变化时,d随r的变化而变化,d与r满足的函数关系是正比例函数关系;
③若n为定值,当r变化时,S随r的变化而变化,S与r满足的函数关系是二次函数关系.
其中正确的是( )
A.①② B.①③ C.②③ D.①②③
4.如图,由等边三角形、正方形、圆组成的轴对称图案中,等边三角形与三个正方形的面积和的比值为( )
A. B.1 C. D.
5.如图,边长为2的正六边形内接于,则它的内切圆半径为( )
A.1 B.2 C. D.
6.如图,是正五边形的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A. B. C. D.
7.如图,正三角形和正方形分别内接于等圆和,若正三角形的周长为m,正方形的周长为n,则m与n的关系为( )
A. B. C. D.不能确定
8.如图,的内接正五边形,点P是上的动点,连接,则的度数为( )
A. B. C. D.随着点P的变化而变化
9.如图,正五边形内接于,连接,,则______°.
10.如图,AC是的内接正六边形的一边,点B在弧AC上,且BC是的内接正十边形的一边,若AB是的内接正n边形的一边,则____.
11.如图,是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与的切点,则的度数为_______°.
12.如图,已知的内接正方形,点F是的中点,与边交于点E,那么____________.
13.如图,平面直角坐标系中,正六边形的顶点A、B在x轴上,顶点F在y轴上,若,求中心P的坐标.
14.如图,六边形ABCDEF是的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分.
(2)设的面积为,六边形ABCDEF的面积为,求的值(结果保留).
答案以及解析
1.答案:B
解析:连接EF,
正五边形ABCDE内接于O点F为BC的中点,
所对的圆心角为,
,
直线AP与O相切于点A,
故选B.
2.答案:A
解析:如图,过A作于C,
∵圆的内接正十二边形的圆心角为,,
∴,
∴,
∴这个圆的内接正十二边形的面积为,
故选:A.
3.答案:D
解析:①,所以与n满足的函数关系是反比例函数关系,正确;
②,所以,所以d与r满足的函数关系是正比例函数关系,正确;
③,所以S与r满足的函数关系是二次函数关系,正确.
故选D.
4.答案:A
解析:如图,设圆的圆心为O,过A作于于D,则AD必过点O,且;
的边长为,则,,,
∴正方形的边长为,面积为,三个正方形的面积和为,
的面积为,
∴等边三角形与三个正方形的面积和的比值为.
故选A.
5.答案:D
解析:如图,连接,,作于G,
∵,,
∴是等边三角形,
∴,
∵,
∴,
∴,
即它的内切圆半径为,
故选:D.
6.答案:D
解析:是正五边形的外接圆,
,
∵,,
,,
∴,即,故B不符合题意;D符合题意;
,即,故C不符合题意;
,即,故A不符合题意;
故选:D.
7.答案:A
解析:设等圆和的半径为r,如图,,
正三角形和正方形分别内接于等圆和,
∴,,
,,,
,,
,
,
,
;
故选A.
8.答案:A
解析:连接,
是的内接正五边形,
,,
,,
,
,
在与中,
,
,
,
,
,
故选:A.
9.答案:
解析:∵五边形是正五边形,
∴,,
∴,
故答案为:.
10.答案:15
解析:连接OB,是的内接正六边形的一边,
,
是的内接正十边形的一边,
,
,
即,,
故答案为15.
11.答案:36
解析:如图,连接OM,ON.
M,N,F分别是AE,AB,CD与的切点,
,,
,
,
,
,
故答案为:36.
12.答案:
解析:如图所示,连接,交于点G,连接,
的内接正方形,
经过点O,
点F是的中点,
,
设,则
,
,
,
故答案为:.
13.答案:
解析:连接、,过点P作轴于Q,
六边形是正六边形,,
,,,,
,是等边三角形,,
,,,
,
,
中心P的坐标为.
14.答案:(1)证明见解析
(2)
解析:(1)证明:如图,连接AE,AD,AC,
六边形ABCDEF是的内接正六边形,
,
,
,
过顶点A的三条对角线四等分.
(2)如图,过点O作于点G,连接OE.
设的半径为R,
,,
是边长为R的等边三角形,
六边形ABCDEF的周长.
在中,,,
利用勾股定理得,
正六边形ABCDEF的面积.
的面积,
.
