3.7切线长定理 同步练习 (含详解) 2024-2025学年九年级数学北师大版下册
文档属性
| 名称 | 3.7切线长定理 同步练习 (含详解) 2024-2025学年九年级数学北师大版下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 00:00:00 | ||
图片预览



文档简介
3.7切线长定理 同步练习
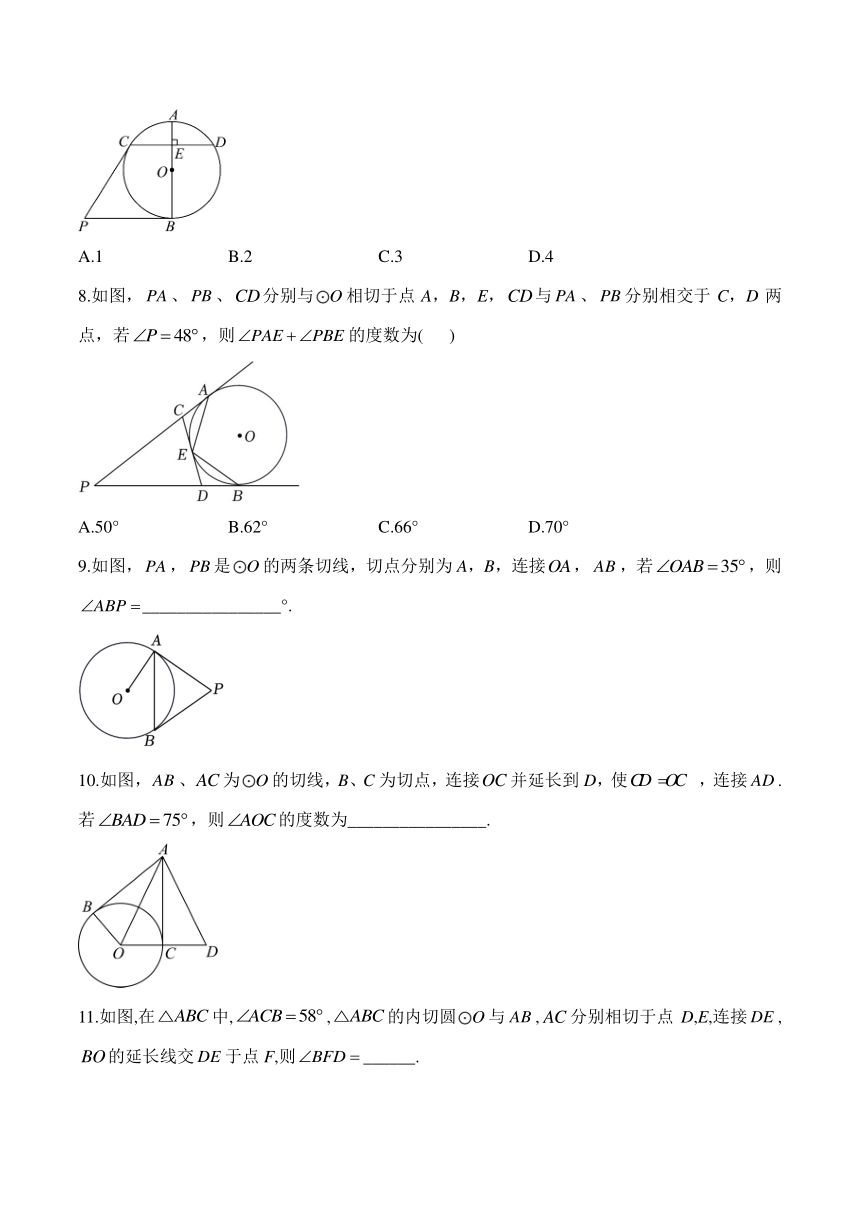
1.如图,P为外一点,PA、PB分别切于点A、B,CD切于点E,分别交PA、PB于点C、D,若,则的周长为( )
A.8 B.6 C.12 D.10
2.如图,已知半圆O与四边形的边相切,切点分别为D,E,C,设半圆的半径为2,,则四边形的周长为( )
A.7 B.9 C.12 D.14
3.如图,PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若的周长为8,OP=5,则⊙O的半径为( )
A.2 B.3 C.4 D.不能确定
4.如图,等边三角形的边长为8,以上一点O为圆心的圆分别与边,相切,则的半径为( )
A. B.3 C.4 D.
5.如图,,是的切线,切点为A,D,点B,C在上,若,则( )
A. B. C. D.
6.如图,是的直径,,分别与相切于点A,点C,若,,则的长为( )
A.1 B.2 C. D.
7.如图,为的直径,,分别与相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( )
A.1 B.2 C.3 D.4
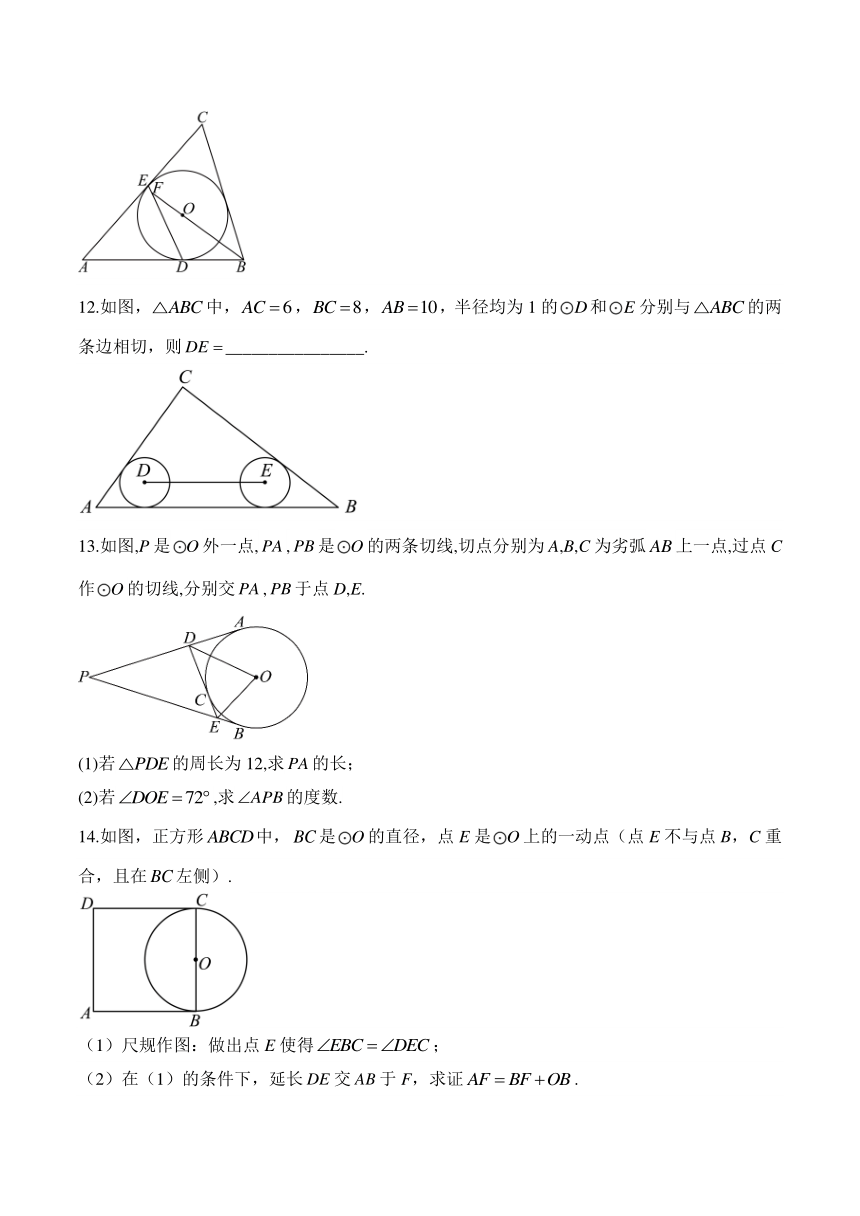
8.如图,、、分别与相切于点A,B,E,与、分别相交于C,D两点,若,则的度数为( )
A.50° B.62° C.66° D.70°
9.如图,,是的两条切线,切点分别为A,B,连接,,若,则________________°.
10.如图,、为的切线,B、C为切点,连接并延长到D,使,连接.若,则的度数为________________.
11.如图,在中,,的内切圆与,分别相切于点D,E,连接,的延长线交于点F,则______.
12.如图,中,,,,半径均为1的和分别与的两条边相切,则________________.
13.如图,P是外一点,,是的两条切线,切点分别为A,B,C为劣弧上一点,过点C作的切线,分别交,于点D,E.
(1)若的周长为12,求的长;
(2)若,求的度数.
14.如图,正方形中,是的直径,点E是上的一动点(点E不与点B,C重合,且在左侧).
(1)尺规作图:做出点E使得;
(2)在(1)的条件下,延长交于F,求证.
答案以及解析
1.答案:C
解析:∵PA、PB分别切于点A、B,CD切于点E,
,,,
,
即的周长为12,
故选:C.
2.答案:D
解析:∵半圆O与四边形的边相切,切点分别为D,E,C,
∴,
∴,
∵,
∴四边形是周长.
故选:D.
3.答案:B
解析:连接OA.
PA、PB、DE分别切⊙O于A、B、C点,
BD=CD,CE=AE,PA=PB,.
的周长为2AP=8
AP=4
在直角三角形OAP中,根据勾股定理,得AO==3,
⊙O的半径为3.
故选:B.
4.答案:A
解析:设与的切点为E,
连接,,
等边三角形的边长为8,
,,
圆分别与边,相切,
,
,
,
,
,
的半径为,
故选:A.
5.答案:C
解析:如图,连接,
四边形是的内接四边形,
,
,
,
即,
,
,是的切线,根据切线长定理得,
,
,
.
故选:C.
6.答案:B
解析:,分别与相切于点A,点C,
,
,
是等边三角形,
,,
与相切于点A,
,
,
,
是直径,
,
,
,
故选:B.
7.答案:C
解析:作于H,
直径于H,
,
,分别切于C,B,
,直径,
四边形是矩形,
,,
,
,
.
故选:C.
8.答案:C
解析:、、分别切于A、B、E,交、于C、D两点,
,,
,,
,,
,,
即,,
,
.
故选:C.
9.答案:
解析:,是的两条切线,
,,
,
,
,
.
故答案为:.
10.答案:/65度
解析:、为的切线,B、C为切点,
,,
是的平分线,
,
,
是等腰三角形,
是的角平分线,
,
,
,
,
故答案为:.
11.答案:/29度
解析:的内切圆与,分别相切于点D,E,
,,
,
,
∵,
,
故答案为:.
12.答案:5
解析:设和分别与的两条边相切的切点分别为G,N,H,K,连接DN,DG,EH,EK
,,,
则,,
作于点F,于点M,
中,,,,,
,
是直角三角形,
,
四边形,四边形,四边形都是矩形,
,,,
设,,
则
,,
,
,
设,,
,
,
,
,
解得,
则.
故答案为5.
13.答案:(1)6
(2)
解析:(1)由切线长定理可知,,,.
则的周长.
.
(2)如图,连接,,,
则,.
.
在四边形中,,,
即,
.
14.答案:(1)见解析
(2)见解析
解析:(1)如图,连接,作的垂直平分线,交于点K,以K为圆心,
为半径作圆,交于一点,该点即为所求作的点E;
连接、,、,,
四边形为正方形,
,
为的直径,
又直径所对的圆周角为直角,
点C在上,
是的直径,
,
为的直径,
,
,
,
,
,
.
(2)证明:延长交于点G,如图所示:
为的直径,
,
,,
,为半径,
、为的切线,
,
,
四边形为正方形,
,,
,
,
,
,
,
,
为半径,
为的切线,
,
,
,,
垂直平分,
,
,
,
即,
,,
,
,
,
.
1.如图,P为外一点,PA、PB分别切于点A、B,CD切于点E,分别交PA、PB于点C、D,若,则的周长为( )
A.8 B.6 C.12 D.10
2.如图,已知半圆O与四边形的边相切,切点分别为D,E,C,设半圆的半径为2,,则四边形的周长为( )
A.7 B.9 C.12 D.14
3.如图,PA,PB,DE分别切⊙O于点A,B,C,过C的切线分别交PA,PB于点E,D,若的周长为8,OP=5,则⊙O的半径为( )
A.2 B.3 C.4 D.不能确定
4.如图,等边三角形的边长为8,以上一点O为圆心的圆分别与边,相切,则的半径为( )
A. B.3 C.4 D.
5.如图,,是的切线,切点为A,D,点B,C在上,若,则( )
A. B. C. D.
6.如图,是的直径,,分别与相切于点A,点C,若,,则的长为( )
A.1 B.2 C. D.
7.如图,为的直径,,分别与相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( )
A.1 B.2 C.3 D.4
8.如图,、、分别与相切于点A,B,E,与、分别相交于C,D两点,若,则的度数为( )
A.50° B.62° C.66° D.70°
9.如图,,是的两条切线,切点分别为A,B,连接,,若,则________________°.
10.如图,、为的切线,B、C为切点,连接并延长到D,使,连接.若,则的度数为________________.
11.如图,在中,,的内切圆与,分别相切于点D,E,连接,的延长线交于点F,则______.
12.如图,中,,,,半径均为1的和分别与的两条边相切,则________________.
13.如图,P是外一点,,是的两条切线,切点分别为A,B,C为劣弧上一点,过点C作的切线,分别交,于点D,E.
(1)若的周长为12,求的长;
(2)若,求的度数.
14.如图,正方形中,是的直径,点E是上的一动点(点E不与点B,C重合,且在左侧).
(1)尺规作图:做出点E使得;
(2)在(1)的条件下,延长交于F,求证.
答案以及解析
1.答案:C
解析:∵PA、PB分别切于点A、B,CD切于点E,
,,,
,
即的周长为12,
故选:C.
2.答案:D
解析:∵半圆O与四边形的边相切,切点分别为D,E,C,
∴,
∴,
∵,
∴四边形是周长.
故选:D.
3.答案:B
解析:连接OA.
PA、PB、DE分别切⊙O于A、B、C点,
BD=CD,CE=AE,PA=PB,.
的周长为2AP=8
AP=4
在直角三角形OAP中,根据勾股定理,得AO==3,
⊙O的半径为3.
故选:B.
4.答案:A
解析:设与的切点为E,
连接,,
等边三角形的边长为8,
,,
圆分别与边,相切,
,
,
,
,
,
的半径为,
故选:A.
5.答案:C
解析:如图,连接,
四边形是的内接四边形,
,
,
,
即,
,
,是的切线,根据切线长定理得,
,
,
.
故选:C.
6.答案:B
解析:,分别与相切于点A,点C,
,
,
是等边三角形,
,,
与相切于点A,
,
,
,
是直径,
,
,
,
故选:B.
7.答案:C
解析:作于H,
直径于H,
,
,分别切于C,B,
,直径,
四边形是矩形,
,,
,
,
.
故选:C.
8.答案:C
解析:、、分别切于A、B、E,交、于C、D两点,
,,
,,
,,
,,
即,,
,
.
故选:C.
9.答案:
解析:,是的两条切线,
,,
,
,
,
.
故答案为:.
10.答案:/65度
解析:、为的切线,B、C为切点,
,,
是的平分线,
,
,
是等腰三角形,
是的角平分线,
,
,
,
,
故答案为:.
11.答案:/29度
解析:的内切圆与,分别相切于点D,E,
,,
,
,
∵,
,
故答案为:.
12.答案:5
解析:设和分别与的两条边相切的切点分别为G,N,H,K,连接DN,DG,EH,EK
,,,
则,,
作于点F,于点M,
中,,,,,
,
是直角三角形,
,
四边形,四边形,四边形都是矩形,
,,,
设,,
则
,,
,
,
设,,
,
,
,
,
解得,
则.
故答案为5.
13.答案:(1)6
(2)
解析:(1)由切线长定理可知,,,.
则的周长.
.
(2)如图,连接,,,
则,.
.
在四边形中,,,
即,
.
14.答案:(1)见解析
(2)见解析
解析:(1)如图,连接,作的垂直平分线,交于点K,以K为圆心,
为半径作圆,交于一点,该点即为所求作的点E;
连接、,、,,
四边形为正方形,
,
为的直径,
又直径所对的圆周角为直角,
点C在上,
是的直径,
,
为的直径,
,
,
,
,
,
.
(2)证明:延长交于点G,如图所示:
为的直径,
,
,,
,为半径,
、为的切线,
,
,
四边形为正方形,
,,
,
,
,
,
,
,
为半径,
为的切线,
,
,
,,
垂直平分,
,
,
,
即,
,,
,
,
,
.
