3.1 圆 同步练习 (含详解)2024-2025学年九年级数学北师大版下册
文档属性
| 名称 | 3.1 圆 同步练习 (含详解)2024-2025学年九年级数学北师大版下册 |  | |
| 格式 | docx | ||
| 文件大小 | 644.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 20:17:15 | ||
图片预览




文档简介
3.1圆 同步练习
1.下列语句是有关几何作图的叙述:
①以O为圆心作弧;
②延长射线AB到点C;
③作∠AOB,使∠AOB=∠1;
④作直线AB,使AB=a;
⑤延长线段AB到C,使BC=AB.
其中正确的数量是( )
A.1个 B.2个 C.3个 D.4个
2.下列命题中,正确的有( )
①直径是弦,但弦不一定是直径;
②半圆是弧,但弧不一定是半圆;
③半径相等的两个圆是等圆;
④一条弦把圆分成的两段弧中,至少有一段是优弧;
⑤长度相等的两条弧是等弧.
A.1个 B.2个 C.3个 D.4个
3.如图,在两个同心圆中,,分别是大圆和小圆的直径,且与不在同一条直线上,则可直接判定以点A,C,B,D为顶点的四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.一组对边平行且相等 D.对角线互相平分
4.在平面直角坐标系中,是以点为圆心,5为半径的圆.则下列说法正确的是( )
A.原点O在外 B.原点O在内 C.原点O在上 D.无法确定
5.定义:点P、点Q分别为两个图形、上任一点,如果线段的长度存在最小值时,就称该最小值为图形和的“近距离”;如果线段的长度存在最大值时,就称该最大值为图形和的“远距离”.线段和是平面直角坐标系中的两个图形,其中,点,,半径为1.下列关于线段与的“距离”说法,正确的是( )
A.“近距离”是4 B.“近距离”是5 C.“远距离”是6 D.“远距离”是8
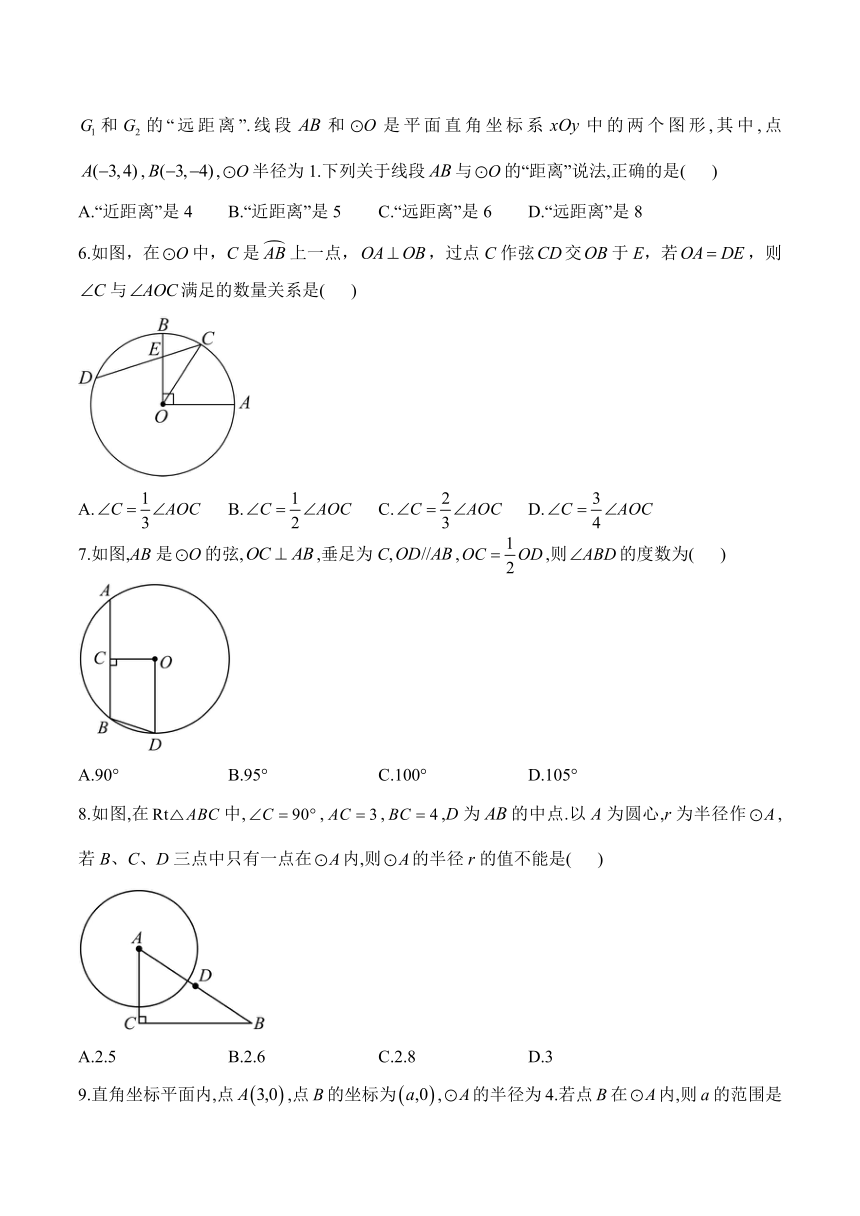
6.如图,在中,C是上一点,,过点C作弦交于E,若,则与满足的数量关系是( )
A. B. C. D.
7.如图,AB是的弦,,垂足为C,,,则的度数为( )
A.90° B.95° C.100° D.105°
8.如图,在中,,,,D为的中点.以A为圆心,r为半径作,若B、C、D三点中只有一点在内,则的半径r的值不能是( )
A.2.5 B.2.6 C.2.8 D.3
9.直角坐标平面内,点,点B的坐标为,的半径为4.若点B在内,则a的范围是______.
10.如图,的直径,半径,点D在弧上,,,垂足分别为E、F,若点E为的中点,弧的度数为______.
11.如图,已知矩形的边,,现以点A为圆心作圆,如果B,C,D至少有一点在圆内,且至少有一点在圆外,那么半径r的取值范围是______.
12.如图,点P为上一动点,点A为圆内一点,且满足,当最大时,则的长是______.
13.如图,以的AB边为直径作半圆,交BC于点D,交AC于点E,若,,求的度数.
14.定义:点P、点Q分别为两个图形、上任一点,如果线段PQ的长度存在最小值时,就称该最小值为图形和的“近距离”;如果线段PQ的长度存在最大值时,就称该最大值为图形和的“远距离”.
请你在理解上述定义的基础上,解决下面问题:
在平面直角坐标系xOy中,点,,,.
(1)直接写出线段AB与线段CD的“近距离”是______,“远距离”是______;
(2)设半径为1,直接写出与四边形ABCD的“近距离”是______,“远距离”______;
(3)若的半径为,且圆心M在射线.上移动,当与四边形ABCD的“近距离”不大于时,求与四边形ABCD的“远距离”d的取值范围.
答案以及解析
1.答案:B
解析:①以O为圆心作弧,因为半径不固定,可以作出无数条弧,则原叙述错误;
②射线是由A向B无限延伸,则原叙述错误;
③基本作图:作一个角等于已知角可知,可以作,使,则原叙述正确;
④直线可以向两方无限延伸,不可度量,则原叙述错误;
⑤基本作图:作线段,可以延长线段到,使,则原叙述正确;
综上,正确的数量是2个,
故选:B.
2.答案:C
解析:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径,直径是圆中最长的弦,直径是弦,但弦不一定是直径,故①说法正确,符合题意;
圆上任意两点间的部分叫做弧,半圆是弧,但弧不一定是半圆,故②说法正确,符合题意;
半径决定圆的大小,半径相等的两个圆是等圆,故③说法正确,符合题意;
弧可以分为劣弧、优弧、半圆三种,当一条弦是直径时,直径把圆分成两个半圆,既不是优弧也不是劣弧,故④说法不正确,不符合题意;
长度相等的两条弧只有弧所在的半径也相同或相等时才是等弧,故⑤说法错误,不符合题意;
综上所述,正确的选项有①②③,正确的个数共3个,
故选:C.
3.答案:D
解析:在两个同心圆中,,分别是大圆和小圆的直径,且与不在同一条直线上,
∴,,
∴四边形是平行四边形
故选:D
4.答案:C
解析:∵点P的坐标是,
∴,
而的半径为5,
∴等于圆的半径,
∴点P在上.
故选:C.
5.答案:C
解析:如图所示,
E点距离线段最近,为与线段的近距离,,,
F点距离线段最远,为与线段的远距离,,,
,
.
故选:C.
6.答案:C
解析:连接,
,
,
,,
,
,
,,
,
;
故选C.
7.答案:D
解析:如图:连接OB,
∴,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∴.
故选D.
8.答案:A
解析:∵在中,,,
∴,
∵D为的中点,
∴.
当的半径时,点D在上,点C、B在圆外,
当的半径时,点C在上,点D在圆内,点B在圆外,
当的半径时,点B在上,点C、D在圆内,
当的半径满足时,点D在内,
当的半径满足时,点C、D在内,
当的半径满足时,点B、C、D在内,
∴若B、C、D三点中只有一点在内,
则的半径r的取值范围是.
故选:A.
9.答案:/
解析:由题意知,,
∵点B在内,
∴,即,
解得,,
故答案为:.
10.答案:/度
解析:如图所示,连接,交于点G,
∵,,,
∴四边形是矩形,
∴
∵点E为的中点,
∴
∴
∴是等边三角形,
∴,即弧的度数为
故答案为:.
11.答案:
解析:如图,连结,,
四边形是矩形,
,
,
以点A为圆心作圆,如果B、C、D至少有一点在圆内,
,
至少有一点在圆外,
,
半径r的取值范围是:.
故答案为:.
12.答案:
解析:如图,过作于,,
∴,
∴最大,则最大,
∴此时,
∴,
故答案为:
13.答案:
解析:,.
,..
,.
,,.
14.答案:(1)6,10
(2)2,6
(3)
解析:(1)观察图象可知,线段AB与线段CD的“近距离”是6,“远距离”是10.
故答案为6,10.
(2)由图1可知,与四边形ABCD的“近距离”是2,“远距离”是6,故答案为2,6.
(3)如图2中,
当和时,与四边形ABCD的近距离恰为
由于,,可知此时:与四边形ABCD的远距离为
与四边形ABCD的远距离为
.
1.下列语句是有关几何作图的叙述:
①以O为圆心作弧;
②延长射线AB到点C;
③作∠AOB,使∠AOB=∠1;
④作直线AB,使AB=a;
⑤延长线段AB到C,使BC=AB.
其中正确的数量是( )
A.1个 B.2个 C.3个 D.4个
2.下列命题中,正确的有( )
①直径是弦,但弦不一定是直径;
②半圆是弧,但弧不一定是半圆;
③半径相等的两个圆是等圆;
④一条弦把圆分成的两段弧中,至少有一段是优弧;
⑤长度相等的两条弧是等弧.
A.1个 B.2个 C.3个 D.4个
3.如图,在两个同心圆中,,分别是大圆和小圆的直径,且与不在同一条直线上,则可直接判定以点A,C,B,D为顶点的四边形是平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.一组对边平行且相等 D.对角线互相平分
4.在平面直角坐标系中,是以点为圆心,5为半径的圆.则下列说法正确的是( )
A.原点O在外 B.原点O在内 C.原点O在上 D.无法确定
5.定义:点P、点Q分别为两个图形、上任一点,如果线段的长度存在最小值时,就称该最小值为图形和的“近距离”;如果线段的长度存在最大值时,就称该最大值为图形和的“远距离”.线段和是平面直角坐标系中的两个图形,其中,点,,半径为1.下列关于线段与的“距离”说法,正确的是( )
A.“近距离”是4 B.“近距离”是5 C.“远距离”是6 D.“远距离”是8
6.如图,在中,C是上一点,,过点C作弦交于E,若,则与满足的数量关系是( )
A. B. C. D.
7.如图,AB是的弦,,垂足为C,,,则的度数为( )
A.90° B.95° C.100° D.105°
8.如图,在中,,,,D为的中点.以A为圆心,r为半径作,若B、C、D三点中只有一点在内,则的半径r的值不能是( )
A.2.5 B.2.6 C.2.8 D.3
9.直角坐标平面内,点,点B的坐标为,的半径为4.若点B在内,则a的范围是______.
10.如图,的直径,半径,点D在弧上,,,垂足分别为E、F,若点E为的中点,弧的度数为______.
11.如图,已知矩形的边,,现以点A为圆心作圆,如果B,C,D至少有一点在圆内,且至少有一点在圆外,那么半径r的取值范围是______.
12.如图,点P为上一动点,点A为圆内一点,且满足,当最大时,则的长是______.
13.如图,以的AB边为直径作半圆,交BC于点D,交AC于点E,若,,求的度数.
14.定义:点P、点Q分别为两个图形、上任一点,如果线段PQ的长度存在最小值时,就称该最小值为图形和的“近距离”;如果线段PQ的长度存在最大值时,就称该最大值为图形和的“远距离”.
请你在理解上述定义的基础上,解决下面问题:
在平面直角坐标系xOy中,点,,,.
(1)直接写出线段AB与线段CD的“近距离”是______,“远距离”是______;
(2)设半径为1,直接写出与四边形ABCD的“近距离”是______,“远距离”______;
(3)若的半径为,且圆心M在射线.上移动,当与四边形ABCD的“近距离”不大于时,求与四边形ABCD的“远距离”d的取值范围.
答案以及解析
1.答案:B
解析:①以O为圆心作弧,因为半径不固定,可以作出无数条弧,则原叙述错误;
②射线是由A向B无限延伸,则原叙述错误;
③基本作图:作一个角等于已知角可知,可以作,使,则原叙述正确;
④直线可以向两方无限延伸,不可度量,则原叙述错误;
⑤基本作图:作线段,可以延长线段到,使,则原叙述正确;
综上,正确的数量是2个,
故选:B.
2.答案:C
解析:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径,直径是圆中最长的弦,直径是弦,但弦不一定是直径,故①说法正确,符合题意;
圆上任意两点间的部分叫做弧,半圆是弧,但弧不一定是半圆,故②说法正确,符合题意;
半径决定圆的大小,半径相等的两个圆是等圆,故③说法正确,符合题意;
弧可以分为劣弧、优弧、半圆三种,当一条弦是直径时,直径把圆分成两个半圆,既不是优弧也不是劣弧,故④说法不正确,不符合题意;
长度相等的两条弧只有弧所在的半径也相同或相等时才是等弧,故⑤说法错误,不符合题意;
综上所述,正确的选项有①②③,正确的个数共3个,
故选:C.
3.答案:D
解析:在两个同心圆中,,分别是大圆和小圆的直径,且与不在同一条直线上,
∴,,
∴四边形是平行四边形
故选:D
4.答案:C
解析:∵点P的坐标是,
∴,
而的半径为5,
∴等于圆的半径,
∴点P在上.
故选:C.
5.答案:C
解析:如图所示,
E点距离线段最近,为与线段的近距离,,,
F点距离线段最远,为与线段的远距离,,,
,
.
故选:C.
6.答案:C
解析:连接,
,
,
,,
,
,
,,
,
;
故选C.
7.答案:D
解析:如图:连接OB,
∴,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∴.
故选D.
8.答案:A
解析:∵在中,,,
∴,
∵D为的中点,
∴.
当的半径时,点D在上,点C、B在圆外,
当的半径时,点C在上,点D在圆内,点B在圆外,
当的半径时,点B在上,点C、D在圆内,
当的半径满足时,点D在内,
当的半径满足时,点C、D在内,
当的半径满足时,点B、C、D在内,
∴若B、C、D三点中只有一点在内,
则的半径r的取值范围是.
故选:A.
9.答案:/
解析:由题意知,,
∵点B在内,
∴,即,
解得,,
故答案为:.
10.答案:/度
解析:如图所示,连接,交于点G,
∵,,,
∴四边形是矩形,
∴
∵点E为的中点,
∴
∴
∴是等边三角形,
∴,即弧的度数为
故答案为:.
11.答案:
解析:如图,连结,,
四边形是矩形,
,
,
以点A为圆心作圆,如果B、C、D至少有一点在圆内,
,
至少有一点在圆外,
,
半径r的取值范围是:.
故答案为:.
12.答案:
解析:如图,过作于,,
∴,
∴最大,则最大,
∴此时,
∴,
故答案为:
13.答案:
解析:,.
,..
,.
,,.
14.答案:(1)6,10
(2)2,6
(3)
解析:(1)观察图象可知,线段AB与线段CD的“近距离”是6,“远距离”是10.
故答案为6,10.
(2)由图1可知,与四边形ABCD的“近距离”是2,“远距离”是6,故答案为2,6.
(3)如图2中,
当和时,与四边形ABCD的近距离恰为
由于,,可知此时:与四边形ABCD的远距离为
与四边形ABCD的远距离为
.
