3.5确定圆的条件 同步练习(含答案)2024-2025学年九年级数学北师大版(2012)下册
文档属性
| 名称 | 3.5确定圆的条件 同步练习(含答案)2024-2025学年九年级数学北师大版(2012)下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 21:03:40 | ||
图片预览



文档简介
3.5确定圆的条件 同步练习
1.如图2,在平面直角坐标系中,点A,B,C的坐标为、、,则外接圆的圆心坐标是( )
A. B. C. D.
2.三角形的外心具有的性质是( )
A.外心在三角形外 B.外心在三角形内
C.外心到三角形三边距离相等 D.外心到三角形三个顶点距离相等
3.平面上有4个点,它们不在同一直线上,过其中3个点作圆,可以作出不重复的圆n个,则n的值不可能为( )
A.4 B.3 C.2 D.1
4.在中,若两条直角边的长分别为6和8,则这个三角形的外接圆半径为( )
A.3 B.4 C.5 D.6
5.船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔.只要留心从船上到两个灯塔间的角度不超过一定的大小,就不用担心触礁.如图所示的网格是正方形网格,点A,B,C,D,P,M,N是网格线交点,当船航行到点的位置时,此时与两个灯塔M,N间的角度(的大小)一定无触礁危险.那么,对于A,B,C,D四个位置,船处于___________时,也一定无触礁危险.( )
A.位置A B.位置B C.位置C D.位置D
6.有一题目:“已知和有相同的外心,,求.”两人的说法如下:甲:的度数是;乙:甲考虑的不全,的度数还应有一个不同的值.下列判断正确的是( )
A.甲和乙都对 B.甲对乙错 C.甲错乙对 D.甲和乙都错
7.如图,在等腰直角中,,,点E是边上一点(点E不与点A,B重合),连接,线段绕点C顺时针旋转得到线段,连接,,线段与边交于点F,有以下说法:
Ⅰ四边形的面积总等于;
Ⅱ当时,的外接圆半径为.
下列判断正确的是( )
A.两种说法都正确 B.说法Ⅰ正确,说法Ⅱ不正确
C.说法Ⅰ不正确,说法Ⅱ正确 D.两种说法都不正确
8.中,,是的外接圆,于点D,关于点D对称得到.若线段与有两个公共点,则满足的条件是( )
A. B.
C. D.
9.已知在中,,,则的外接圆的半径是__________.
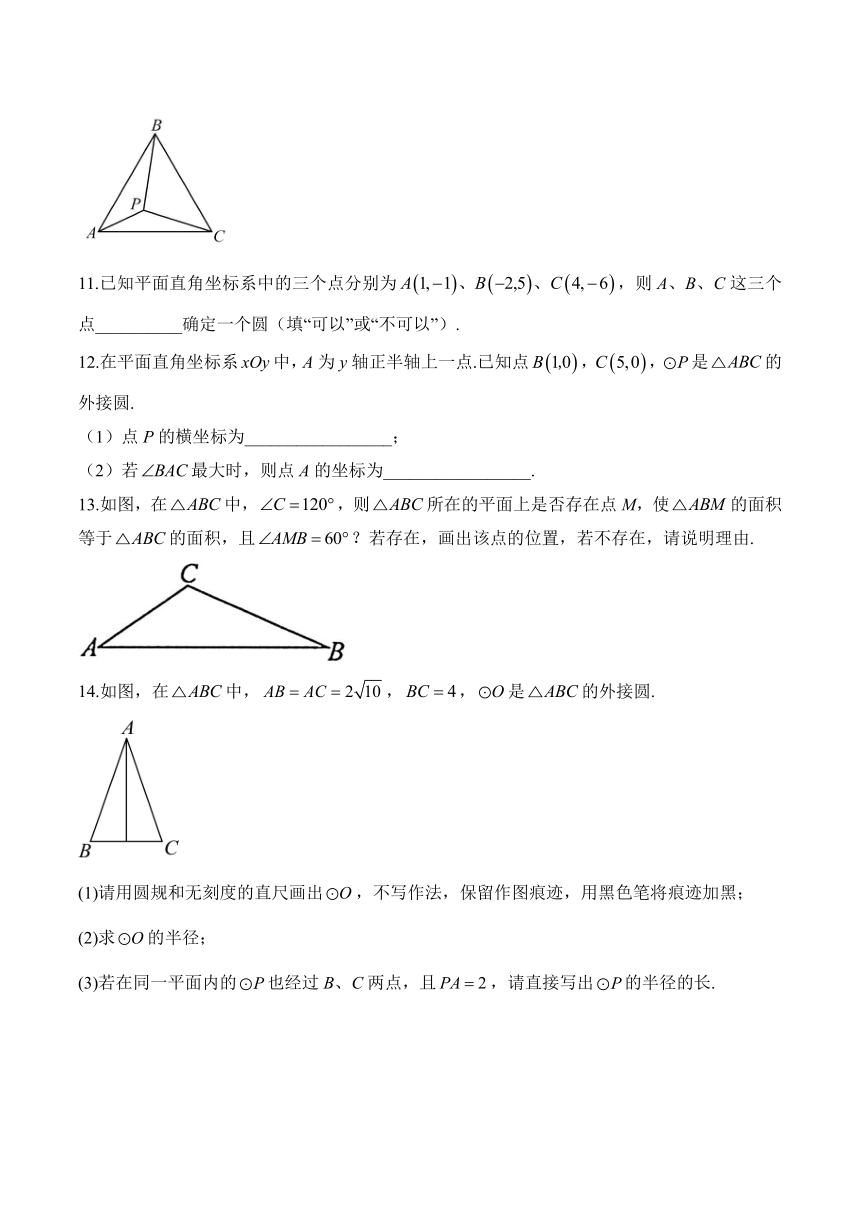
10.如图,为等边三角形,,若P为内一动点,且满足,则线段长度的最小值为______.
11.已知平面直角坐标系中的三个点分别为,则A、B、C这三个点__________确定一个圆(填“可以”或“不可以”).
12.在平面直角坐标系中,A为y轴正半轴上一点.已知点,,是的外接圆.
(1)点P的横坐标为_________________;
(2)若最大时,则点A的坐标为_________________.
13.如图,在中,,则所在的平面上是否存在点M,使的面积等于的面积,且?若存在,画出该点的位置,若不存在,请说明理由.
14.如图,在中,,,是的外接圆.
(1)请用圆规和无刻度的直尺画出,不写作法,保留作图痕迹,用黑色笔将痕迹加黑;
(2)求的半径;
(3)若在同一平面内的也经过B、C两点,且,请直接写出的半径的长.
答案以及解析
1.答案:D
解析:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点即为圆心,且坐标是.
故选:D.
2.答案:D
解析:A.外心不一定在三角形外,错误;
B.外心不一定在三角形内,错误;
C.外心到三角形三角距离相等,错误;
D.外心到三角形三个顶点距离相等,正确;
故选:D.
3.答案:C
解析:分为三种情况:①当四点都在同一个圆上时,如图1,此时,
②当三点在一直线上时,如图2,
分别过A、B、C或A、C、D或A、B、D作圆,共3个圆,即,
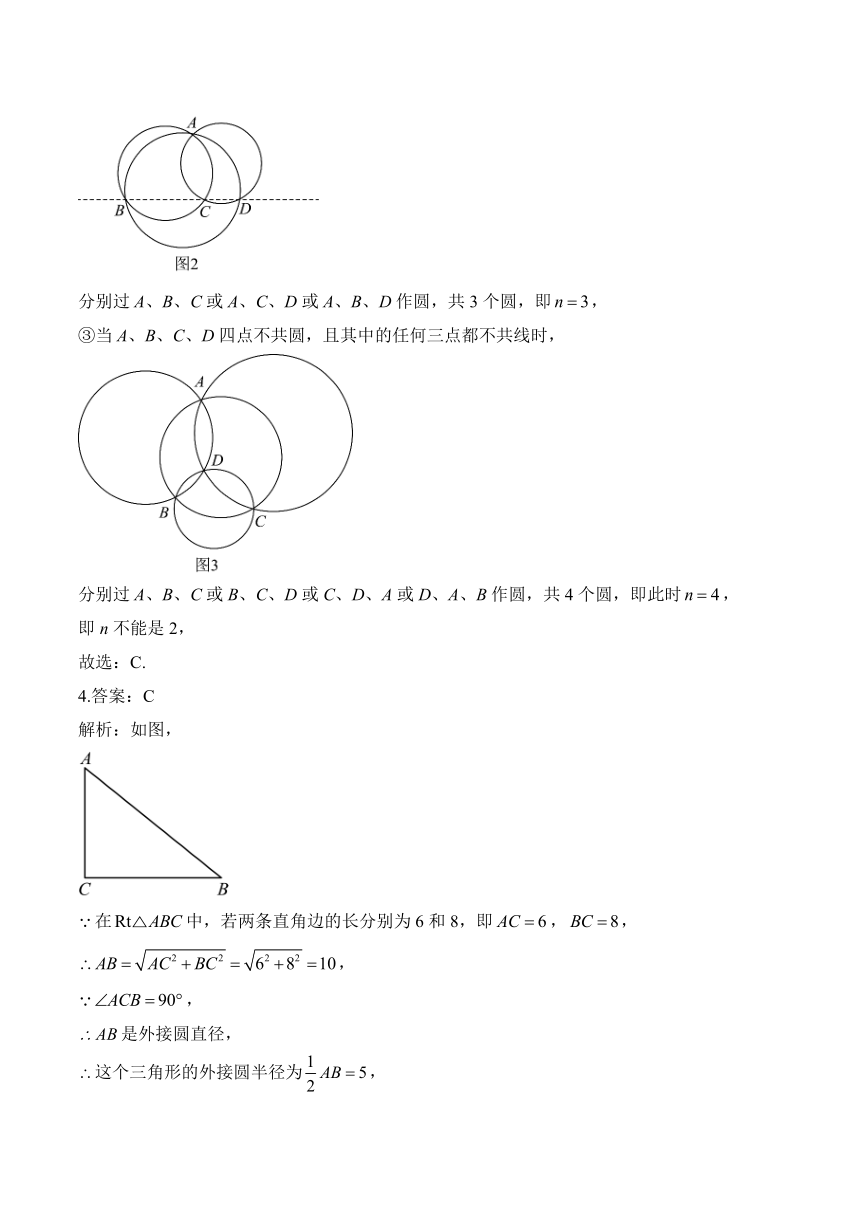
③当A、B、C、D四点不共圆,且其中的任何三点都不共线时,
分别过A、B、C或B、C、D或C、D、A或D、A、B作圆,共4个圆,即此时,
即n不能是2,
故选:C.
4.答案:C
解析:如图,
在中,若两条直角边的长分别为6和8,即,,
,
,
是外接圆直径,
这个三角形的外接圆半径为,
故选:C.
5.答案:B
解析:如图,
由网格可知,点O是和垂直平分线的交点,
即点O是的外接圆的圆心,
,
点M在的外接圆上,
,
船处于位置B时,也一定无触礁危险,
故选B.
6.答案:C
解析:
画出图形,当点D,C在的不同侧时,
,
;
当点D,在的同一侧时,
,
综上所述,的度数为或,
甲错乙对,
故选:C.
7.答案:A
解析:(Ⅰ)在等腰直角中,,,
线段绕点C顺时针旋转得到线段,
,,
,
在与中,
,
,
四边形的面积的面积;
(Ⅱ),,
,
,
,,
,
,
,
,
,
,
的外接圆半径为,
综上分析可知,两种说法都正确,故A正确.
故选:A.
8.答案:C
解析:如图,当与切于点F时,此时线段与有且只有一个公共点,
连接,,
是的外接圆,于点D,
为直径,,
,
关于点D对称得到,
,
,
;
当从点B在中点时,由题意可知,,为等腰直角三角形,
,
;
此时,点E与点C重合,线段与有两个公共点,
此时当点B继续逆时针向点A运动时(不与A重合),线段与有且只有一个公共点,
综上,线段与有两个公共点时,满足的条件是.
故选:C.
9.答案:
解析:如图,作,垂足为D,则O一定在上,
,
设,
即,
解得.
故答案为:.
10.答案:
解析:如图,作的外接圆,
∴当B,P,O三点在同一直线上时最小.连接,,,交于点M,在优弧上找一点D,
连接,,
∵,
∴,
∴,
∴为等边三角形,
∵为等边三角形,
∴四边形为菱形,
∴,
∵,
∴,
∴,,
∴,
∴的最小值为.
故答案为:;
11.答案:可以
解析:设直线的解析式为,
把,代入得,
,
解得,,
所以直线的解析式为,
当时,,
所以点不在直线上,
即点A、B、C不在同一条直线上,
所以过A、B、C这三个点能确定一个圆.
故答案为:可以
12.答案:(1)
(2)
解析:(1)点,,
的中点坐标为,
是的外接圆,
点M在的垂直平分线上,
点P的横坐标为3,
故答案为3;
(2)连接,,根据(1)可知点P一定在直线上,
是的外接圆,A为y轴正半轴上,
,,
如图,过点P作于点N,
,
,,
,
,
,
,
当最小时,最大,即最大,即最大,
当,即当与y轴相切于点A时,最大,
连接,
与y轴相切于点A,
轴,
四边形是矩形,
,,
在中,,
,
点A的坐标为,
故答案为:.
13.答案:存在点M,图见解析
解析:存在点M,如图,
构造等边三角形ABE,作等边的外接圆,过点C作AB的平行线交于点和,
,
,
,
和是符合题意的点,
分别作和关于AB的对称点和,则点和也符合题意,
故符合题意的点有4个,分别为、、和.
14.答案:(1)见解析
(2)
(3)或
解析:(1)如图所示:
(2)过点A作,垂足为D,连接、,
,,
垂直平分,
,
点O在的垂直平分线上,即O在上,
,
,
在中,,,
,
设,则.
在中,,
,即.
解得,
即的半径为;
(3)当也经过B、C两点,
则设,
,则或,
,
或.
所以的半径的长为或.
1.如图2,在平面直角坐标系中,点A,B,C的坐标为、、,则外接圆的圆心坐标是( )
A. B. C. D.
2.三角形的外心具有的性质是( )
A.外心在三角形外 B.外心在三角形内
C.外心到三角形三边距离相等 D.外心到三角形三个顶点距离相等
3.平面上有4个点,它们不在同一直线上,过其中3个点作圆,可以作出不重复的圆n个,则n的值不可能为( )
A.4 B.3 C.2 D.1
4.在中,若两条直角边的长分别为6和8,则这个三角形的外接圆半径为( )
A.3 B.4 C.5 D.6
5.船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔.只要留心从船上到两个灯塔间的角度不超过一定的大小,就不用担心触礁.如图所示的网格是正方形网格,点A,B,C,D,P,M,N是网格线交点,当船航行到点的位置时,此时与两个灯塔M,N间的角度(的大小)一定无触礁危险.那么,对于A,B,C,D四个位置,船处于___________时,也一定无触礁危险.( )
A.位置A B.位置B C.位置C D.位置D
6.有一题目:“已知和有相同的外心,,求.”两人的说法如下:甲:的度数是;乙:甲考虑的不全,的度数还应有一个不同的值.下列判断正确的是( )
A.甲和乙都对 B.甲对乙错 C.甲错乙对 D.甲和乙都错
7.如图,在等腰直角中,,,点E是边上一点(点E不与点A,B重合),连接,线段绕点C顺时针旋转得到线段,连接,,线段与边交于点F,有以下说法:
Ⅰ四边形的面积总等于;
Ⅱ当时,的外接圆半径为.
下列判断正确的是( )
A.两种说法都正确 B.说法Ⅰ正确,说法Ⅱ不正确
C.说法Ⅰ不正确,说法Ⅱ正确 D.两种说法都不正确
8.中,,是的外接圆,于点D,关于点D对称得到.若线段与有两个公共点,则满足的条件是( )
A. B.
C. D.
9.已知在中,,,则的外接圆的半径是__________.
10.如图,为等边三角形,,若P为内一动点,且满足,则线段长度的最小值为______.
11.已知平面直角坐标系中的三个点分别为,则A、B、C这三个点__________确定一个圆(填“可以”或“不可以”).
12.在平面直角坐标系中,A为y轴正半轴上一点.已知点,,是的外接圆.
(1)点P的横坐标为_________________;
(2)若最大时,则点A的坐标为_________________.
13.如图,在中,,则所在的平面上是否存在点M,使的面积等于的面积,且?若存在,画出该点的位置,若不存在,请说明理由.
14.如图,在中,,,是的外接圆.
(1)请用圆规和无刻度的直尺画出,不写作法,保留作图痕迹,用黑色笔将痕迹加黑;
(2)求的半径;
(3)若在同一平面内的也经过B、C两点,且,请直接写出的半径的长.
答案以及解析
1.答案:D
解析:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点即为圆心,且坐标是.
故选:D.
2.答案:D
解析:A.外心不一定在三角形外,错误;
B.外心不一定在三角形内,错误;
C.外心到三角形三角距离相等,错误;
D.外心到三角形三个顶点距离相等,正确;
故选:D.
3.答案:C
解析:分为三种情况:①当四点都在同一个圆上时,如图1,此时,
②当三点在一直线上时,如图2,
分别过A、B、C或A、C、D或A、B、D作圆,共3个圆,即,
③当A、B、C、D四点不共圆,且其中的任何三点都不共线时,
分别过A、B、C或B、C、D或C、D、A或D、A、B作圆,共4个圆,即此时,
即n不能是2,
故选:C.
4.答案:C
解析:如图,
在中,若两条直角边的长分别为6和8,即,,
,
,
是外接圆直径,
这个三角形的外接圆半径为,
故选:C.
5.答案:B
解析:如图,
由网格可知,点O是和垂直平分线的交点,
即点O是的外接圆的圆心,
,
点M在的外接圆上,
,
船处于位置B时,也一定无触礁危险,
故选B.
6.答案:C
解析:
画出图形,当点D,C在的不同侧时,
,
;
当点D,在的同一侧时,
,
综上所述,的度数为或,
甲错乙对,
故选:C.
7.答案:A
解析:(Ⅰ)在等腰直角中,,,
线段绕点C顺时针旋转得到线段,
,,
,
在与中,
,
,
四边形的面积的面积;
(Ⅱ),,
,
,
,,
,
,
,
,
,
,
的外接圆半径为,
综上分析可知,两种说法都正确,故A正确.
故选:A.
8.答案:C
解析:如图,当与切于点F时,此时线段与有且只有一个公共点,
连接,,
是的外接圆,于点D,
为直径,,
,
关于点D对称得到,
,
,
;
当从点B在中点时,由题意可知,,为等腰直角三角形,
,
;
此时,点E与点C重合,线段与有两个公共点,
此时当点B继续逆时针向点A运动时(不与A重合),线段与有且只有一个公共点,
综上,线段与有两个公共点时,满足的条件是.
故选:C.
9.答案:
解析:如图,作,垂足为D,则O一定在上,
,
设,
即,
解得.
故答案为:.
10.答案:
解析:如图,作的外接圆,
∴当B,P,O三点在同一直线上时最小.连接,,,交于点M,在优弧上找一点D,
连接,,
∵,
∴,
∴,
∴为等边三角形,
∵为等边三角形,
∴四边形为菱形,
∴,
∵,
∴,
∴,,
∴,
∴的最小值为.
故答案为:;
11.答案:可以
解析:设直线的解析式为,
把,代入得,
,
解得,,
所以直线的解析式为,
当时,,
所以点不在直线上,
即点A、B、C不在同一条直线上,
所以过A、B、C这三个点能确定一个圆.
故答案为:可以
12.答案:(1)
(2)
解析:(1)点,,
的中点坐标为,
是的外接圆,
点M在的垂直平分线上,
点P的横坐标为3,
故答案为3;
(2)连接,,根据(1)可知点P一定在直线上,
是的外接圆,A为y轴正半轴上,
,,
如图,过点P作于点N,
,
,,
,
,
,
,
当最小时,最大,即最大,即最大,
当,即当与y轴相切于点A时,最大,
连接,
与y轴相切于点A,
轴,
四边形是矩形,
,,
在中,,
,
点A的坐标为,
故答案为:.
13.答案:存在点M,图见解析
解析:存在点M,如图,
构造等边三角形ABE,作等边的外接圆,过点C作AB的平行线交于点和,
,
,
,
和是符合题意的点,
分别作和关于AB的对称点和,则点和也符合题意,
故符合题意的点有4个,分别为、、和.
14.答案:(1)见解析
(2)
(3)或
解析:(1)如图所示:
(2)过点A作,垂足为D,连接、,
,,
垂直平分,
,
点O在的垂直平分线上,即O在上,
,
,
在中,,,
,
设,则.
在中,,
,即.
解得,
即的半径为;
(3)当也经过B、C两点,
则设,
,则或,
,
或.
所以的半径的长为或.
