6.2 直线、射线、线段(第3课时) 课件(共16张PPT)人教版数学七年级上册(2024)
文档属性
| 名称 | 6.2 直线、射线、线段(第3课时) 课件(共16张PPT)人教版数学七年级上册(2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 615.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 17:23:52 | ||
图片预览




文档简介
(共16张PPT)
直线、射线、线段
(第3课时)
1.比较线段长短的方法:
(1)_________;
(2)_________.
度量法
叠合法
2.在数学中,我们常限定用_____________________作图,这就是尺规作图.
无刻度的直尺和圆规
3.关于线段的基本事实:
_____________________________ ;
简单说成:___________________.
两点的所有连线中,线段最短
两点之间,线段最短
4.连接____________的长度,叫作这两点间的距离.
两点的线段
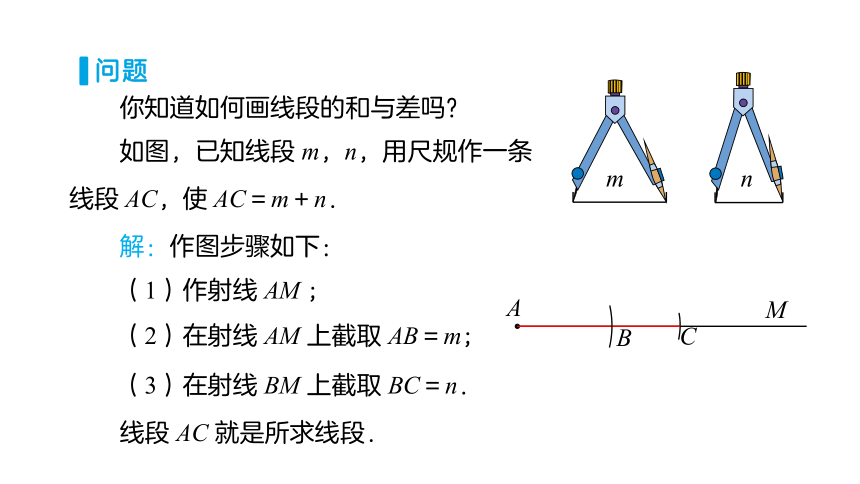
你知道如何画线段的和与差吗?
如图,已知线段 m,n,用尺规作一条线段 AC,使 AC=m+n.
m
n
解:作图步骤如下:
(1)作射线 AM ;
(2)在射线 AM 上截取 AB=m;
A
M
B
(3)在射线 BM 上截取 BC=n.
C
线段 AC 就是所求线段.
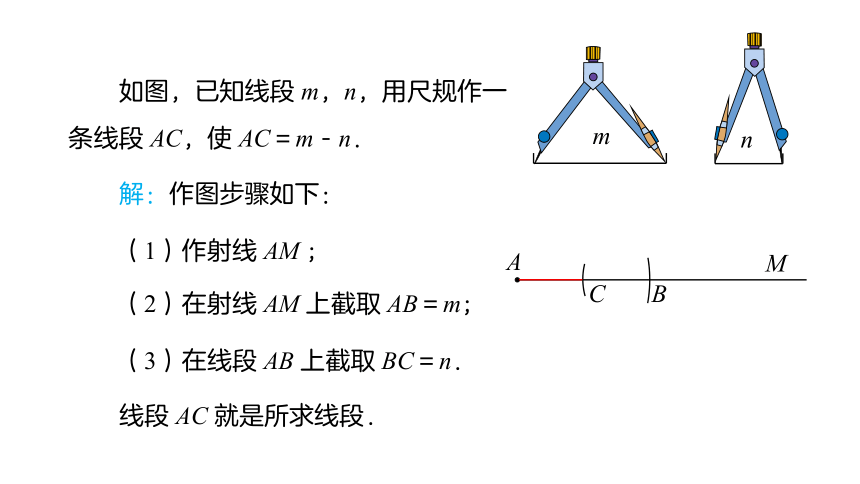
问题
如图,已知线段 m,n,用尺规作一条线段 AC,使 AC=m-n.
m
n
解:作图步骤如下:
(1)作射线 AM ;
(2)在射线 AM 上截取 AB=m;
A
M
C
(3)在线段 AB 上截取 BC=n.
B
线段 AC 就是所求线段.
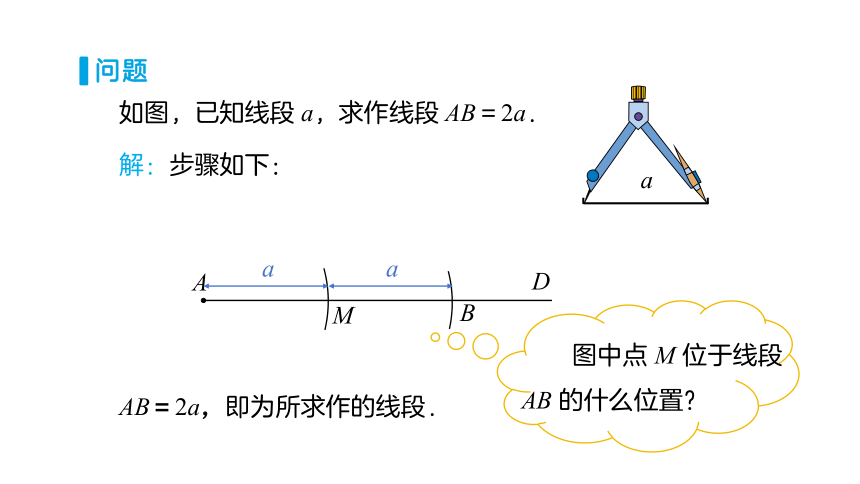
如图,已知线段 a,求作线段 AB=2a.
a
解:步骤如下:
A
D
M
B
a
a
AB=2a,即为所求作的线段.
问题
图中点 M 位于线段AB 的什么位置?
A
M
B
点 M 把线段 AB 分成相等的两条线段 AM 与 MB,点 M 叫作线段 AB 的中点.
数学符号语言:
AM=MB= AB(或 AB=2AM=2BM)
在一张透明的纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点就是线段的中点.
中点
类似地,还有线段的三等分点、四等分点等.
A
M
B
N
AM=MN=NB= AB
AM=MN=NP=PB= AB
A
M
B
N
P
例1 如图,若线段 AB=20 cm,点 C 是线段 AB 上一点,M,N 分别是线段 AC,BC 的中点.
(1)求线段 MN 的长;
A
C
B
M
N
分析:(1)先根据 M,N 分别是线段 AC,BC 的中点得出MC= AC,CN= BC,再由线段 AB=20 cm 即可求出结果.
解:(1)因为 M,N 分别是线段 AC,BC 的中点,
所以 MC= AC,CN= BC.
因为线段 AB=20 cm,
所以 MN=MC+CN= (AC+BC)= AB=10(cm).
A
C
B
M
N
例1 如图,若线段 AB=20 cm,点 C 是线段 AB 上一点,M,N 分别是线段 AC,BC 的中点.
(2)根据(1)中的计算过程和结果,设 AB=a,其他条件不变,你能猜出 MN 的长度吗?请用简洁的语言表达你发现的规律.
分析:(2)由(1)即可得到结论.
A
C
B
M
N
解:(2)由(1)得,
MN=MC+CN= (AC+BC)= AB= a.
即 MN 始终等于 AB 的一半.
A
C
B
M
N
例2 如图,已知线段a,b,作一条线段,使它等于2a-b.
解: 如图,在直线上作线段AB=a,再在线段AB的延长线上作线段BC=a,则线段AC=2a.在线段AC上作线段CD=b,则线段AD=2a-b.
线段的比较与运算
中点、三等分点、四等分点
线段的运算
直线、射线、线段
(第3课时)
1.比较线段长短的方法:
(1)_________;
(2)_________.
度量法
叠合法
2.在数学中,我们常限定用_____________________作图,这就是尺规作图.
无刻度的直尺和圆规
3.关于线段的基本事实:
_____________________________ ;
简单说成:___________________.
两点的所有连线中,线段最短
两点之间,线段最短
4.连接____________的长度,叫作这两点间的距离.
两点的线段
你知道如何画线段的和与差吗?
如图,已知线段 m,n,用尺规作一条线段 AC,使 AC=m+n.
m
n
解:作图步骤如下:
(1)作射线 AM ;
(2)在射线 AM 上截取 AB=m;
A
M
B
(3)在射线 BM 上截取 BC=n.
C
线段 AC 就是所求线段.
问题
如图,已知线段 m,n,用尺规作一条线段 AC,使 AC=m-n.
m
n
解:作图步骤如下:
(1)作射线 AM ;
(2)在射线 AM 上截取 AB=m;
A
M
C
(3)在线段 AB 上截取 BC=n.
B
线段 AC 就是所求线段.
如图,已知线段 a,求作线段 AB=2a.
a
解:步骤如下:
A
D
M
B
a
a
AB=2a,即为所求作的线段.
问题
图中点 M 位于线段AB 的什么位置?
A
M
B
点 M 把线段 AB 分成相等的两条线段 AM 与 MB,点 M 叫作线段 AB 的中点.
数学符号语言:
AM=MB= AB(或 AB=2AM=2BM)
在一张透明的纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点就是线段的中点.
中点
类似地,还有线段的三等分点、四等分点等.
A
M
B
N
AM=MN=NB= AB
AM=MN=NP=PB= AB
A
M
B
N
P
例1 如图,若线段 AB=20 cm,点 C 是线段 AB 上一点,M,N 分别是线段 AC,BC 的中点.
(1)求线段 MN 的长;
A
C
B
M
N
分析:(1)先根据 M,N 分别是线段 AC,BC 的中点得出MC= AC,CN= BC,再由线段 AB=20 cm 即可求出结果.
解:(1)因为 M,N 分别是线段 AC,BC 的中点,
所以 MC= AC,CN= BC.
因为线段 AB=20 cm,
所以 MN=MC+CN= (AC+BC)= AB=10(cm).
A
C
B
M
N
例1 如图,若线段 AB=20 cm,点 C 是线段 AB 上一点,M,N 分别是线段 AC,BC 的中点.
(2)根据(1)中的计算过程和结果,设 AB=a,其他条件不变,你能猜出 MN 的长度吗?请用简洁的语言表达你发现的规律.
分析:(2)由(1)即可得到结论.
A
C
B
M
N
解:(2)由(1)得,
MN=MC+CN= (AC+BC)= AB= a.
即 MN 始终等于 AB 的一半.
A
C
B
M
N
例2 如图,已知线段a,b,作一条线段,使它等于2a-b.
解: 如图,在直线上作线段AB=a,再在线段AB的延长线上作线段BC=a,则线段AC=2a.在线段AC上作线段CD=b,则线段AD=2a-b.
线段的比较与运算
中点、三等分点、四等分点
线段的运算
同课章节目录
