湘教版数学八年级下册 1.3 直角三角形全等的判定 导讲练课件 (共25张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 1.3 直角三角形全等的判定 导讲练课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 21:58:49 | ||
图片预览






文档简介
(共25张PPT)
1.3 直角三角形全等的判定
第一章 直角三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
斜边、直角边定理
三角形全等的判定方法
用尺规作直角三角形
知1-讲
感悟新知
知识点
斜边、直角边定理
1
定理: 斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL” ) .
只适用于直角三角形全等的判
定,对于一般三角形不适用
感悟新知
知1-讲
特别提醒
应用“HL”判定两个直角三角形全等,在书写时两个三角形符号前一定要加上“Rt”.
感悟新知
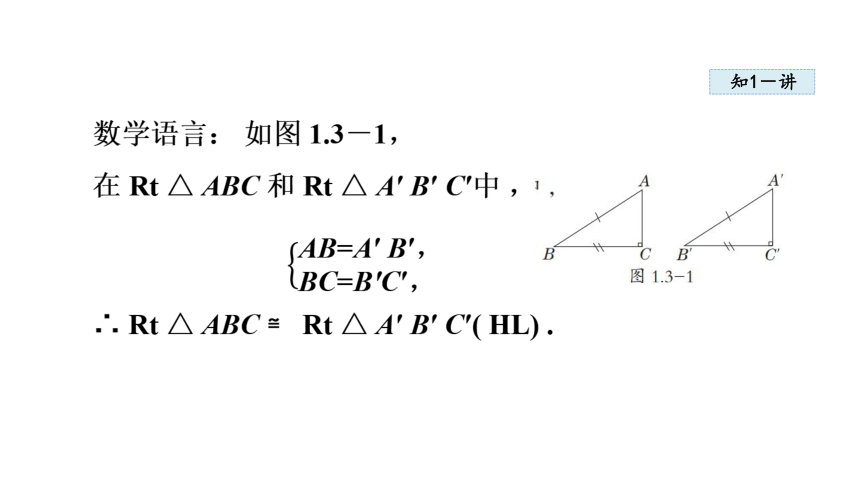
数学语言: 如图 1.3-1,
在 Rt △ ABC 和 Rt △ A′ B′ C′中 ,
∴ Rt △ ABC ≌ Rt △ A′ B′ C′( HL) .
知1-讲
知1-练
感悟新知
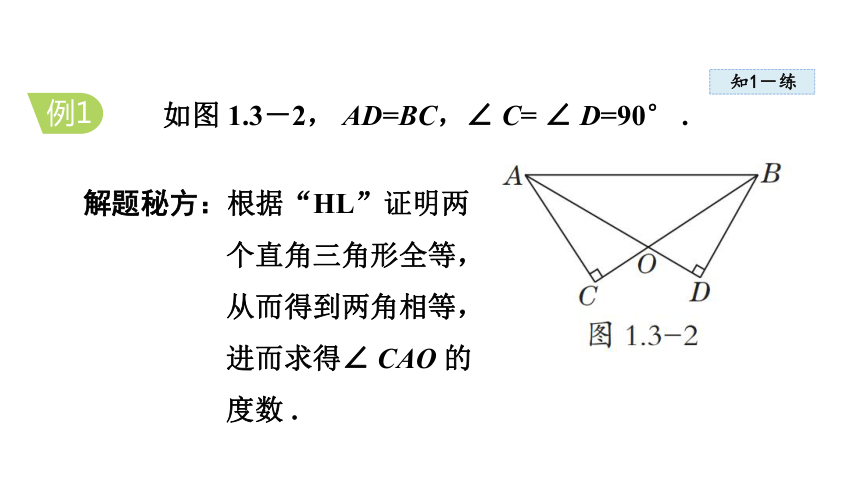
如图 1.3-2, AD=BC,∠ C= ∠ D=90° .
例1
解题秘方:根据“HL”证明两个直角三角形全等,从而得到两角相等,进而求得∠ CAO 的度数 .
知1-练
感悟新知
(1)求证:△ ABC ≌△ BAD;
证明: ∵∠ C= ∠ D=90°,
∴△ ABC 和△ BAD 都是直角三角形 .
在 Rt △ ABC 和 Rt △ BAD 中,
∴ Rt △ ABC ≌ Rt △ BAD( HL) .
利用“HL”判定两个
直角三角形全等时,一定要加上“Rt”
知1-练
感悟新知
(2)若∠ ABC =32°,求∠ CAO 的度数.
解: ∵∠ C=90°,∠ ABC=32°,
∴∠ BAC=58° .
∵ Rt △ ABC ≌ Rt △ BAD,
∴∠ BAD= ∠ ABC=32° .
∴∠ CAO= ∠ BAC - ∠ BAD=58° -32° =26°.
知1-练
感悟新知
方法点拨
证明线段或角相等的步骤:
第一步:观察要证明的线段或角(或通过等量代换得到的线段或角)在哪两个可能全等的三角形中,当待证线段或角不分布在两个全等的三角形中时,常需添加辅助线构造全等三角形;
知1-练
感悟新知
第二步: 分 析 需要证明全等的两个三角形,确定已知条件(包含图形中的隐含条件)是什么,还缺什么条件;
第三步:设法推导出所缺的条件;
第四步:整理书写证明过程 .
感悟新知
知2-讲
知识点
三角形全等的判定方法
2
判定两个三角形全等常用的思路方法如下表:
已知对应
相等的元素 可选择的
判定方法 需寻找的条件
锐角
三角
形或
钝角
三角
形 两边(SS) SSS 或 SAS 可证第三边对应相等或两边的夹角对应相等
一边及其邻
角( SA) SAS 或 ASA或 AAS 可证已知角的另一边对应相等或已知边的另一邻角对应相等或已知边的对角对应相等
感悟新知
知2-讲
锐角
三角
形或
钝角
三角
形 一边及其对角(SA) AAS 可证余下的任意一角对应相等
两角
(AA) ASA 或
AAS 可证两角的夹边对应相等或一相等角的对边对应相等
直角三角形 一锐角
(A) ASA 或
AAS 可证直角与已知锐角的夹边对应相等或已知锐角(或直角)的对边对应相等
感悟新知
知2-讲
直角三角形 斜边(H) HL 或 AAS 可证一条直角边对应相等或一锐角对应相等
一直角边
(L) HL 或 ASA或 AAS 或SAS 可证斜边对应相等或与已知边相邻的锐角对应相等或已知边所对的锐角对应相等或另一直角边对应相等
知2-讲
感悟新知
特别提醒
◆判定一般三角形全等的所有方法对判定两个直角三角形全等同样适用 .
◆在用一般方法证明直角三角形全等时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可 .
感悟新知
知2-练
如图 1.3-3, AB=AC, CD ⊥ AB,垂足为 D, BE ⊥ AC,垂足为 E, CD, BE 相交于点 O. 求证: AO 平分∠ BAC.
例2
知2-练
感悟新知
解题秘方:通过证两次三角形全等解决问题 .
证明: ∵ CD ⊥ AB, BE ⊥ AC,
∴∠ ADC= ∠ AEB=90° .
在△ AEB 和△ ADC 中,
∴△ AEB ≌△ ADC(AAS) , ∴ AE=AD.
知2-练
感悟新知
在 Rt △ AEO 和 Rt △ ADO 中, ∴ Rt △ AEO ≌ Rt △ ADO(HL),
∴∠ EAO= ∠ DAO,
∴ AO 平分∠ BAC.
知2-练
感悟新知
方法点拨
由于直角三角形有一特殊条件——直角,因 此遇到 以下情况要注意:
(1) 有一个锐角和一条边对应相等的两个直角三角形全等;
(2) 两条直角边对应相等的两个直角三角形全等;
(3)在遇到直角三角形的全等问题时,不要忘记隐含的条件——直角相等 .
感悟新知
知3-讲
知识点
用尺规作直角三角形
3
1. 用尺规作直角三角形主要有两种类型: 一类是已知两直角边长;另一类是已知一直角边长和斜边长 .
感悟新知
知3-讲
2. 基本步骤: 第一步: 作直角;
第二步: 在一条直角边上截取长度等于已知直角边长的线段;
第三步: 在另一条直角边上截取长度等于已知的另一条直角边长的线段(或以第二步中弧与直角边的交点为圆心,以已知斜边长为半径画弧交另一条直角边于一点) .
第四步: 连接第二步、第三步中弧与直角边的交点 .
知3-讲
感悟新知
特别解读
用尺规作直角三角形的理论依据是直角三角形全等的判定,其中已知 两直角边依据 “SAS”进行判定;已知一直角边和斜边依据 “HL”进行判定 .
知3-练
感悟新知
如图 1.3 - 4,已知线段 a,求作直角三角形,使一直角边长为 a,斜边长为 3a. (不写作法,保留作图痕迹)
例3
知3-练
感悟新知
方法点拨
已知一直角边和斜边作直角三角形的实质是运用“HL”判定两个直角三角形全等.
知3-练
感悟新知
解: 如图 1.3 - 5,△ ABC 即为所求作的直角三角形 .
解题秘方:紧扣尺规作直角三角形的基本步骤作图 .
直角三角形全等的判定
直角三角形全等的判定
特殊
HL
一般
SAS
ASA
AAS
SSS
1.3 直角三角形全等的判定
第一章 直角三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
斜边、直角边定理
三角形全等的判定方法
用尺规作直角三角形
知1-讲
感悟新知
知识点
斜边、直角边定理
1
定理: 斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL” ) .
只适用于直角三角形全等的判
定,对于一般三角形不适用
感悟新知
知1-讲
特别提醒
应用“HL”判定两个直角三角形全等,在书写时两个三角形符号前一定要加上“Rt”.
感悟新知
数学语言: 如图 1.3-1,
在 Rt △ ABC 和 Rt △ A′ B′ C′中 ,
∴ Rt △ ABC ≌ Rt △ A′ B′ C′( HL) .
知1-讲
知1-练
感悟新知
如图 1.3-2, AD=BC,∠ C= ∠ D=90° .
例1
解题秘方:根据“HL”证明两个直角三角形全等,从而得到两角相等,进而求得∠ CAO 的度数 .
知1-练
感悟新知
(1)求证:△ ABC ≌△ BAD;
证明: ∵∠ C= ∠ D=90°,
∴△ ABC 和△ BAD 都是直角三角形 .
在 Rt △ ABC 和 Rt △ BAD 中,
∴ Rt △ ABC ≌ Rt △ BAD( HL) .
利用“HL”判定两个
直角三角形全等时,一定要加上“Rt”
知1-练
感悟新知
(2)若∠ ABC =32°,求∠ CAO 的度数.
解: ∵∠ C=90°,∠ ABC=32°,
∴∠ BAC=58° .
∵ Rt △ ABC ≌ Rt △ BAD,
∴∠ BAD= ∠ ABC=32° .
∴∠ CAO= ∠ BAC - ∠ BAD=58° -32° =26°.
知1-练
感悟新知
方法点拨
证明线段或角相等的步骤:
第一步:观察要证明的线段或角(或通过等量代换得到的线段或角)在哪两个可能全等的三角形中,当待证线段或角不分布在两个全等的三角形中时,常需添加辅助线构造全等三角形;
知1-练
感悟新知
第二步: 分 析 需要证明全等的两个三角形,确定已知条件(包含图形中的隐含条件)是什么,还缺什么条件;
第三步:设法推导出所缺的条件;
第四步:整理书写证明过程 .
感悟新知
知2-讲
知识点
三角形全等的判定方法
2
判定两个三角形全等常用的思路方法如下表:
已知对应
相等的元素 可选择的
判定方法 需寻找的条件
锐角
三角
形或
钝角
三角
形 两边(SS) SSS 或 SAS 可证第三边对应相等或两边的夹角对应相等
一边及其邻
角( SA) SAS 或 ASA或 AAS 可证已知角的另一边对应相等或已知边的另一邻角对应相等或已知边的对角对应相等
感悟新知
知2-讲
锐角
三角
形或
钝角
三角
形 一边及其对角(SA) AAS 可证余下的任意一角对应相等
两角
(AA) ASA 或
AAS 可证两角的夹边对应相等或一相等角的对边对应相等
直角三角形 一锐角
(A) ASA 或
AAS 可证直角与已知锐角的夹边对应相等或已知锐角(或直角)的对边对应相等
感悟新知
知2-讲
直角三角形 斜边(H) HL 或 AAS 可证一条直角边对应相等或一锐角对应相等
一直角边
(L) HL 或 ASA或 AAS 或SAS 可证斜边对应相等或与已知边相邻的锐角对应相等或已知边所对的锐角对应相等或另一直角边对应相等
知2-讲
感悟新知
特别提醒
◆判定一般三角形全等的所有方法对判定两个直角三角形全等同样适用 .
◆在用一般方法证明直角三角形全等时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可 .
感悟新知
知2-练
如图 1.3-3, AB=AC, CD ⊥ AB,垂足为 D, BE ⊥ AC,垂足为 E, CD, BE 相交于点 O. 求证: AO 平分∠ BAC.
例2
知2-练
感悟新知
解题秘方:通过证两次三角形全等解决问题 .
证明: ∵ CD ⊥ AB, BE ⊥ AC,
∴∠ ADC= ∠ AEB=90° .
在△ AEB 和△ ADC 中,
∴△ AEB ≌△ ADC(AAS) , ∴ AE=AD.
知2-练
感悟新知
在 Rt △ AEO 和 Rt △ ADO 中, ∴ Rt △ AEO ≌ Rt △ ADO(HL),
∴∠ EAO= ∠ DAO,
∴ AO 平分∠ BAC.
知2-练
感悟新知
方法点拨
由于直角三角形有一特殊条件——直角,因 此遇到 以下情况要注意:
(1) 有一个锐角和一条边对应相等的两个直角三角形全等;
(2) 两条直角边对应相等的两个直角三角形全等;
(3)在遇到直角三角形的全等问题时,不要忘记隐含的条件——直角相等 .
感悟新知
知3-讲
知识点
用尺规作直角三角形
3
1. 用尺规作直角三角形主要有两种类型: 一类是已知两直角边长;另一类是已知一直角边长和斜边长 .
感悟新知
知3-讲
2. 基本步骤: 第一步: 作直角;
第二步: 在一条直角边上截取长度等于已知直角边长的线段;
第三步: 在另一条直角边上截取长度等于已知的另一条直角边长的线段(或以第二步中弧与直角边的交点为圆心,以已知斜边长为半径画弧交另一条直角边于一点) .
第四步: 连接第二步、第三步中弧与直角边的交点 .
知3-讲
感悟新知
特别解读
用尺规作直角三角形的理论依据是直角三角形全等的判定,其中已知 两直角边依据 “SAS”进行判定;已知一直角边和斜边依据 “HL”进行判定 .
知3-练
感悟新知
如图 1.3 - 4,已知线段 a,求作直角三角形,使一直角边长为 a,斜边长为 3a. (不写作法,保留作图痕迹)
例3
知3-练
感悟新知
方法点拨
已知一直角边和斜边作直角三角形的实质是运用“HL”判定两个直角三角形全等.
知3-练
感悟新知
解: 如图 1.3 - 5,△ ABC 即为所求作的直角三角形 .
解题秘方:紧扣尺规作直角三角形的基本步骤作图 .
直角三角形全等的判定
直角三角形全等的判定
特殊
HL
一般
SAS
ASA
AAS
SSS
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
