湘教版数学八年级下册 1.2 直角三角形的性质和判定(Ⅱ) 导讲练课件(共51张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 1.2 直角三角形的性质和判定(Ⅱ) 导讲练课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 22:02:43 | ||
图片预览








文档简介
(共51张PPT)
1.2 直角三角形的性质和判定(Ⅱ)
第一章 直角三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
直角三角形三边关系的猜想与验证
勾股定理
勾股定理的应用
勾股定理的逆定理
勾股数
知1-讲
感悟新知
知识点
直角三角形三边关系的猜想与验证
1
1. 常用证法: 验证直角三角形三边之间关系的方法很多,有测量法、几何证明法等,但最常用的是拼图法,即通过拼图构造特殊图形,并根据拼图中各部分面积之间的关系来验证 .
感悟新知
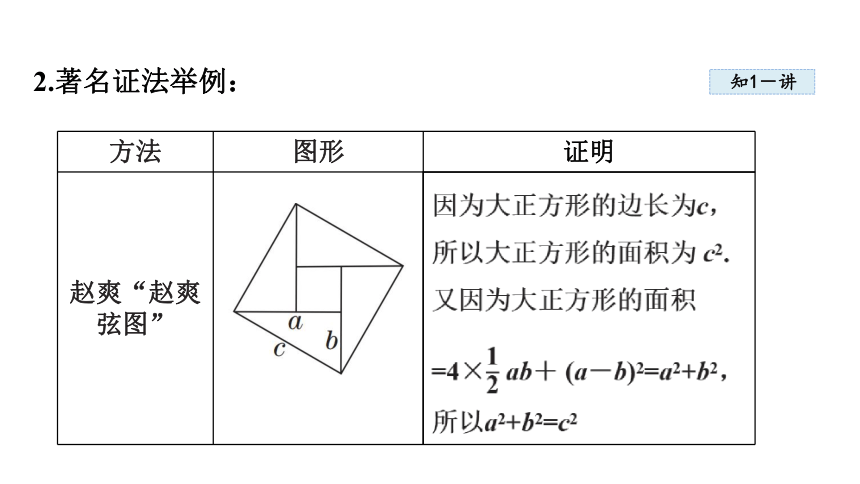
2.著名证法举例:
知1-讲
方法 图形 证明
赵爽“赵爽弦图” 因为大正方形的边长为c,所以大正方形的面积为 c2. 又因为大正方形的面积 =4× ab+ (a-b)2=a2+b2,所以a2+b2=c2
知1-讲
感悟新知
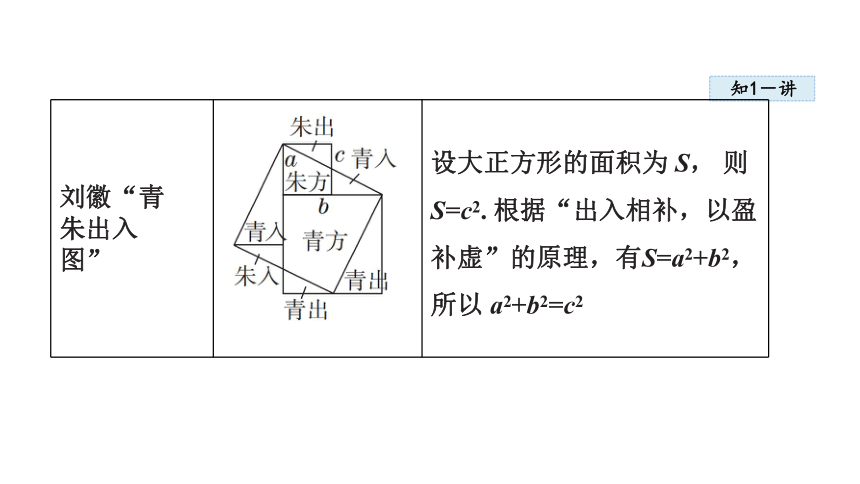
刘徽“青
朱出入
图” 设大正方形的面积为 S, 则 S=c2. 根据“出入相补,以盈补虚”的原理,有S=a2+b2, 所以 a2+b2=c2
知1-讲
感悟新知
加菲尔德
总统拼图 设梯形的面积为 S,则
S= (a+b) (a+b)=a2+b2+ab. 又S= ab+ ab+ c2=c2+ab,所以 a2+b2=c2
毕达哥拉
斯拼图 由图①得大正方形的面积 =c2+4× ab,由图②得大正方形的面积 =a2+b2+4× ab,比较两式易得 a2+b2=c2
感悟新知
知1-讲
特别提醒
用拼图法证明直角三角形三边关系的思路:
(1) 将图形进行割补拼接形成特殊图形,注意割补拼接时图形之间没有重叠、没有空隙;
(2) 根据同一种图形的面积的不同表示方法列出等式;
(3) 利用等式性质验证结论成立,即拼出图形→写出表示图形面积的式子→找出等量关系→恒等变形→推导结论 .
感悟新知
知1-练
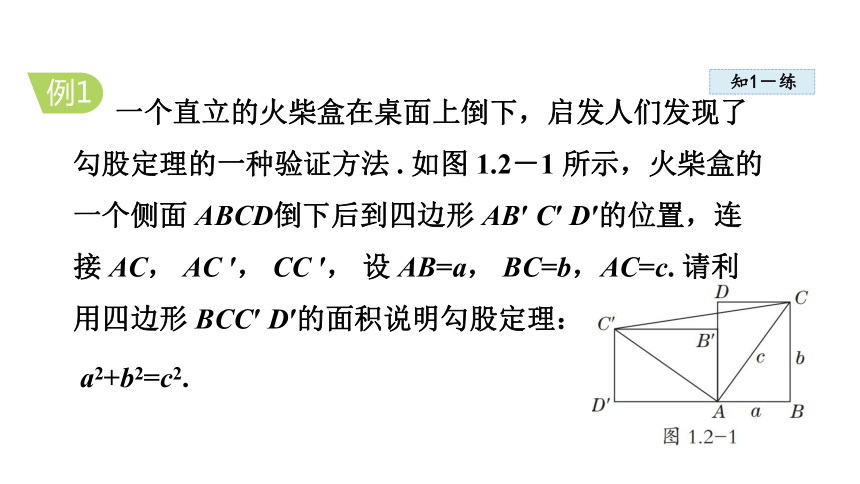
一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种验证方法 . 如图 1.2-1 所示,火柴盒的一个侧面 ABCD倒下后到四边形 AB′ C′ D′的位置,连接 AC, AC ′, CC ′, 设 AB=a, BC=b,AC=c. 请利用四边形 BCC′ D′的面积说明勾股定理:
a2+b2=c2.
例1
知1-练
感悟新知
证明: 易知四边形 BCC′ D′为直角梯形,
∴ S 梯形 BCC′ D′ = ( BC+C′ D′ ) · BD′ = .
易得 Rt △ ABC ≌ Rt △ AB′ C′,
∴ AC′ =AC=c,∠ BAC= ∠ B′ AC′ .
∴ ∠ CAC′ =∠ CAB′ +∠ B′ AC′ =∠ CAB′ +∠ BAC=90° .
解题秘方:紧扣“总体面积等于各部分面积之和”进行证明 .
知1-练
感悟新知
详解
Rt△ AB′C′是四边形ABCD中Rt△ABC倒下得到的,因此两个三角形的形状、大小相 同, 所以Rt△ABC≌Rt△AB′C′.
知1-练
感悟新知
整个图形面积等于不重叠、无空隙的各组成部分的面积的和 .
∴ S 梯形 BCC′ D′ =S △ ABC+S △ CAC′ +S △ D′ AC′
= ab+ c2+ ab= .
∴ = , ∴ a2+b2=c2.
感悟新知
知2-讲
知识点
勾股定理
2
1.直角三角形的性质定理: 直角三角形两直角边 a, b 的平方和,等于斜边 c 的平方 . 即 a2+b2=c2.
古人称直角三角形的直角边中较短的一边为勾,较长的一边为股,斜边为弦,因此这一性质被称为勾股定理 .
感悟新知
知2-讲
数学语言: 如图 1.2-2,在 Rt △ ABC 中,
∠ C=90°, AB=c, AC=b, BC=a,则 a2+b2=c2.
2.勾股定理的变形公式: a2=c2- b2; b2=c2 - a2.
知2-讲
感悟新知
特别提醒
1. 勾股定理揭示的是直角三角形的三边的平方关系, 只有在直角三角形中才可以使用勾股定理 .
2. 利用勾股定理,可以在已知直角三角形任意两边的长时求出第三边的长 .
3. 运用勾股定理时,若未确定哪条边是斜边,则要分类讨论,写出所有可能,以免漏解或错解 .
感悟新知
知2-讲
3. 基本思想方法: 勾股定理把“形”与“数”有机地结合起来,即把直角三角形这一“形”与三边关系这一“数”结合起来,它是数形结合思想的典范 .
感悟新知
知2-练
例2
在 Rt △ ABC 中 , ∠ A,∠ B,∠ C 的对边分别为 a, b,c,∠ C=90° .
解题秘方:利用勾股定理解答 .
知1-练
感悟新知
(1)已知 a=3, b=4, 求 c;
解: ∵∠ C=90°, a=3, b=4,
∴由勾股定理,得 c2===5.
知1-练
感悟新知
(2)已知 c=19, a=13,求 b(结果保留根号).
解:∵∠ C=90°, c=19, a=13,
∴由勾股定理,得 b2===8
知1-练
感悟新知
(3)已知 a ∶ b=1 ∶ 2, c=5,求 b.
解:∵ a ∶ b=1 ∶ 2, ∴ b=2a.
又∵∠ C=90°, c=5,
∴由勾股定理,得 a2+(2a) 2=52,
解得 a= (负值舍去) . ∴ b=2 .
知2-练
感悟新知
解法提醒
分清待求的是斜边还是直角边,以便合理选择是直接用勾股定理还是用勾股定理的变形公式 .
若求斜边,则直接用勾股定理;若求直角边,则用勾股定理的变形公式 .
感悟新知
知2-练
[ 中考·齐齐哈尔 ] 若直角三角形其中两条边的长分别为 3,4,则该直角三角形斜边上的高的长为 ________.
例3
解题秘方:紧扣“所给的较长边可能是直角边或斜边”进行分类解答 .
知2-练
感悟新知
解: 若直角三角形的两直角边长分别为 3,4,
则斜边长为 =5.
设直角三角形斜边上的高为 h,
则×3×4= ×5h,解得 h=2.4.
若直角三角形一条直角边长为 3,斜边长为 4,
则另一条直角边长为 = .
知2-练
感悟新知
答案:2.4 或
设直角三角形斜边上的高为 h1,
则×3× = ×4h1,解得 h1= .
综上所述,该直角三角形斜边上的高的长为 2.4 或.
知2-练
感悟新知
特别警示
当题中没有图或没有指明哪条边长是斜边长时,需要分类讨论,此题容易忽略4是斜边长的情况 .
知2-练
感悟新知
方法点拨
直接求直角三角形的边长时一般借助勾股定理求,但一定要分清楚直角边和斜边,若问题没有明确直角边和斜边,则要进行分类讨论 .
感悟新知
知3-讲
知识点
勾股定理的应用
3
1.勾股定理的应用范围:
勾股定理是直角三角形的一个重要性质,它把直角三角形有一个直角的“形”的特点转化为三边“数”的关系 . 利用勾股定理,可以解决与直角三角形有关的计算和证明问题,还可以解决生活、生产中的一些实际问题 .
感悟新知
知3-讲
2.勾股定理的应用的常见类型:
(1) 已知直角三角形的任意两边求第三边;
(2)已知直角三角形的任意一边确定另两边的关系;
(3)证明包含平方(算术平方根)关系的几何问题;
(4)求解几何体表面上的最短路程问题;
(5)构造方程(或方程组)计算有关线段长度, 解决生产、生活中的实际问题 .
知3-讲
感悟新知
特别提醒
运用勾股定理解决实际问题的一般步骤:
(1) 从实际问题中抽象出几何图形 .
(2) 确定要求的线段所在的直角三角形 .
(3) 找准直角边和斜边, 根据勾股定理建立等量关系并列出等式 .
(4)求得结果 .
知3-练
感悟新知
如图 1.2 - 3,在△ ABC 中,∠ C=90°, AC=2,点 D在 BC 上,∠ ADC=2 ∠ B, AD= ,则 BC 的长为 ________.
例4
解题秘方:紧扣三角形外角的性质及勾股定理解题 .
知3-练
感悟新知
答案: +1
解:∵∠ ADC=2 ∠ B,∠ ADC= ∠ B+ ∠ BAD,∴∠ B= ∠ BAD,
∴ BD=AD= .
∴在 Rt △ ACD 中, CD= =1,
∴ BC= +1.
知3-练
感悟新知
解法提醒
本题通过角的倍数关系得到边的相等关系,以及利用勾股定理求解 .
知3-练
感悟新知
[ 中考·南通 ] 如图 1.2 - 4,一艘轮船位于灯塔 P 的南偏东 60°方向,距离灯塔 P50 海里的 A 处,它沿正北方向航行一段时间后,到达位于灯塔 P的北偏东 45°方向上的 B 处,此时 B 处与灯塔 P的距离为 海里(结果保留根号) .
例5
知3-练
感悟新知
解: 如图 1.2 - 4,过点 P 作 PC ⊥ AB 于点 C.
在 Rt △ APC 中, AP=50 海里, ∠ APC=90° -60° =30°,∴ AC= AP=25 海里,
∴ PC= =25 (海里) .
解题秘方:将实际问题通过建模转化为直角三角形问题,然后利用勾股定理求解.
知3-练
感悟新知
答案:25
在 Rt △ PCB 中,∠ BPC=90° - 45° =45°,
∴∠ B=45° = ∠ BPC,∴ BC=PC=25 3海里,
∴ PB= =25 (海里) .
知3-练
感悟新知
方法点拨
求三角形的边或高时,可通过作辅助线构造直角三角形,用勾股定理来解决问题 .
感悟新知
知4-讲
知识点
勾股定理的逆定理
4
1. 勾股定理的逆定理: 如果三角形的三条边长 a, b, c 满足关系: a2+b2=c2 ,那么这个三角形是直角三角形 .
感悟新知
知4-讲
2. 利用边的关系判定直角三角形的步骤:
(1) “找”: 找出三角形三边中的最长边 .
(2)“算”: 计算较短两边的平方和与最长边的平方 .
(3)“判”: 若两者相等,则这个三角形是直角三角形;否则不是 .
感悟新知
知4-讲
3.勾股定理与其逆定理的关系:
定理 勾股定理 勾股定理的逆定理
区别 (1)勾股定理是以“一个三角
形是直角三角形”为条件,进
而得到这个直角三角形三边长
的关系,即 a2+b2=c2( c 为斜
边长);
(2)勾股定理是根据直角三角
形探求边的关系,体现了由形到数的转化 (1)勾股定理的逆定理是以“一个三角形的三边长a, b,c 满足 a2+b2=c2”为条件,进而得到这个三角形为直角三角形;
(2)勾股定理的逆定理是由三角形的三边关系探求三角形的形状,体现了由数到形的转化
感悟新知
知4-讲
联系 勾股定理与勾股定理的逆定理的条件和结论相反,勾股定理是直角三角形的性质,而其逆定理是直角三角形的判定,勾股定理及其逆定理都与直角三角形有关
知4-讲
感悟新知
特别提醒
◆勾股定理的逆定理是判定直角三角形的一个依据,在判定时不能说“在直角三角形中”“直角边”“斜边”,因为还没有确定是直角三角形 .
◆ a2+b2=c2 只 是 一 种表现形式,满足a2=b2+c2 或b2=a2+c2 的也是直角三角形,只是这时a或b为斜边 .
感悟新知
知4-练
判断满足下列条件的三角形是不是直角三角形:
(1)在△ ABC 中,∠ A=25° ,∠ C=65° ;
(2)在△ ABC 中, AC=12, AB=20, BC=16;
(3)一个三角形的三边长 a, b, c 满足 a∶ b∶ c=1∶1∶ 2 .
例6
知4-练
感悟新知
解题秘方:紧扣直角三角形的判定方法解题 .
解: (1)在△ ABC 中,
∵∠ A+ ∠ C=25° +65° =90°,
∴△ ABC 是直角三角形 .
知4-练
感悟新知
(2)在△ ABC 中,∵ AC2+BC2=122+162=202=AB2,
∴△ ABC 是直角三角形 .
(3)设 a=x,则 b=x, c= x.
∵ x2+x2= ( x ) 2,即 a2+b2=c2,
∴这个三角形是直角三角形 .
注意: 这个三角形也是
等腰三角形
知4-练
感悟新知
方法点拨
判断一个三角形是不是直角三角形的方法:
(1) 当已知条件与角度有关时,一般通过计算看 该三角形中是否有两 个角互余来判断;
(2)当已知条件与边有关时,一般通过计算 看 较 短两边的平方和是否等于最长边的平 方来判断 .
感悟新知
知5-讲
知识点
勾股数
5
1.勾股数: 满足 a2+b2=c2 的三个正整数称为勾股数 .
勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方 .
勾股数有无数组
感悟新知
知5-讲
2. 判别一组数是否为勾股数的一般步骤:
(1)“看”: 看是不是三个正整数;
(2)“找”: 找最大数;
(3)“算”: 计算最大数的平方与两个较小数的平方和;
(4)“判”: 若两者相等,则这三个数是一组勾股数;否则,不是一组勾股数 .
知5-讲
感悟新知
特别提醒
一组勾股数中的各数都乘相同的倍数可以得到一组新的勾股数:如3, 4, 5是勾股数,则6, 8, 10和9,12,15也是勾股数,即如果a, b, c是一组勾股数,那么na,nb, nc ( n 为正整数)也是一组勾股数 .
感悟新知
知5-练
下面四组数中是勾股数的一组是( )
A.6,7,8
B.5,8,13
C.1.5,2,2.5
D.21,28,35
例7
知5-练
感悟新知
答案:D
解题秘方:紧扣勾股数必须同时满足的两个条件进行判断 .
解:A.62+72 ≠ 82,故不是勾股数; B.52+82 ≠ 132,故不是勾股数; C.1.5 和 2.5 不是正整数,故不是勾股数; D.21,28,35 是正整数,且 212+282=352,故是勾股数.故选 D.
知5-练
感悟新知
方法点拨
确定勾股数的方法:
首先看这三个数是否是正整数, 然后看较小的两个数的平方和是否等于最大数的平方,记住常见的勾股数( 3,4, 5; 5, 12, 13; 8,15, 17; 7, 24, 25 )可以提高解题速度 .
直角三角形的性质和判定(Ⅱ)
三边平方关系
勾股定理的
逆定理
实际应用
几何应用
勾股定理
拼图法
面积法
验证
条件
结论
直角三角形
互逆定理
应用
1.2 直角三角形的性质和判定(Ⅱ)
第一章 直角三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
直角三角形三边关系的猜想与验证
勾股定理
勾股定理的应用
勾股定理的逆定理
勾股数
知1-讲
感悟新知
知识点
直角三角形三边关系的猜想与验证
1
1. 常用证法: 验证直角三角形三边之间关系的方法很多,有测量法、几何证明法等,但最常用的是拼图法,即通过拼图构造特殊图形,并根据拼图中各部分面积之间的关系来验证 .
感悟新知
2.著名证法举例:
知1-讲
方法 图形 证明
赵爽“赵爽弦图” 因为大正方形的边长为c,所以大正方形的面积为 c2. 又因为大正方形的面积 =4× ab+ (a-b)2=a2+b2,所以a2+b2=c2
知1-讲
感悟新知
刘徽“青
朱出入
图” 设大正方形的面积为 S, 则 S=c2. 根据“出入相补,以盈补虚”的原理,有S=a2+b2, 所以 a2+b2=c2
知1-讲
感悟新知
加菲尔德
总统拼图 设梯形的面积为 S,则
S= (a+b) (a+b)=a2+b2+ab. 又S= ab+ ab+ c2=c2+ab,所以 a2+b2=c2
毕达哥拉
斯拼图 由图①得大正方形的面积 =c2+4× ab,由图②得大正方形的面积 =a2+b2+4× ab,比较两式易得 a2+b2=c2
感悟新知
知1-讲
特别提醒
用拼图法证明直角三角形三边关系的思路:
(1) 将图形进行割补拼接形成特殊图形,注意割补拼接时图形之间没有重叠、没有空隙;
(2) 根据同一种图形的面积的不同表示方法列出等式;
(3) 利用等式性质验证结论成立,即拼出图形→写出表示图形面积的式子→找出等量关系→恒等变形→推导结论 .
感悟新知
知1-练
一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种验证方法 . 如图 1.2-1 所示,火柴盒的一个侧面 ABCD倒下后到四边形 AB′ C′ D′的位置,连接 AC, AC ′, CC ′, 设 AB=a, BC=b,AC=c. 请利用四边形 BCC′ D′的面积说明勾股定理:
a2+b2=c2.
例1
知1-练
感悟新知
证明: 易知四边形 BCC′ D′为直角梯形,
∴ S 梯形 BCC′ D′ = ( BC+C′ D′ ) · BD′ = .
易得 Rt △ ABC ≌ Rt △ AB′ C′,
∴ AC′ =AC=c,∠ BAC= ∠ B′ AC′ .
∴ ∠ CAC′ =∠ CAB′ +∠ B′ AC′ =∠ CAB′ +∠ BAC=90° .
解题秘方:紧扣“总体面积等于各部分面积之和”进行证明 .
知1-练
感悟新知
详解
Rt△ AB′C′是四边形ABCD中Rt△ABC倒下得到的,因此两个三角形的形状、大小相 同, 所以Rt△ABC≌Rt△AB′C′.
知1-练
感悟新知
整个图形面积等于不重叠、无空隙的各组成部分的面积的和 .
∴ S 梯形 BCC′ D′ =S △ ABC+S △ CAC′ +S △ D′ AC′
= ab+ c2+ ab= .
∴ = , ∴ a2+b2=c2.
感悟新知
知2-讲
知识点
勾股定理
2
1.直角三角形的性质定理: 直角三角形两直角边 a, b 的平方和,等于斜边 c 的平方 . 即 a2+b2=c2.
古人称直角三角形的直角边中较短的一边为勾,较长的一边为股,斜边为弦,因此这一性质被称为勾股定理 .
感悟新知
知2-讲
数学语言: 如图 1.2-2,在 Rt △ ABC 中,
∠ C=90°, AB=c, AC=b, BC=a,则 a2+b2=c2.
2.勾股定理的变形公式: a2=c2- b2; b2=c2 - a2.
知2-讲
感悟新知
特别提醒
1. 勾股定理揭示的是直角三角形的三边的平方关系, 只有在直角三角形中才可以使用勾股定理 .
2. 利用勾股定理,可以在已知直角三角形任意两边的长时求出第三边的长 .
3. 运用勾股定理时,若未确定哪条边是斜边,则要分类讨论,写出所有可能,以免漏解或错解 .
感悟新知
知2-讲
3. 基本思想方法: 勾股定理把“形”与“数”有机地结合起来,即把直角三角形这一“形”与三边关系这一“数”结合起来,它是数形结合思想的典范 .
感悟新知
知2-练
例2
在 Rt △ ABC 中 , ∠ A,∠ B,∠ C 的对边分别为 a, b,c,∠ C=90° .
解题秘方:利用勾股定理解答 .
知1-练
感悟新知
(1)已知 a=3, b=4, 求 c;
解: ∵∠ C=90°, a=3, b=4,
∴由勾股定理,得 c2===5.
知1-练
感悟新知
(2)已知 c=19, a=13,求 b(结果保留根号).
解:∵∠ C=90°, c=19, a=13,
∴由勾股定理,得 b2===8
知1-练
感悟新知
(3)已知 a ∶ b=1 ∶ 2, c=5,求 b.
解:∵ a ∶ b=1 ∶ 2, ∴ b=2a.
又∵∠ C=90°, c=5,
∴由勾股定理,得 a2+(2a) 2=52,
解得 a= (负值舍去) . ∴ b=2 .
知2-练
感悟新知
解法提醒
分清待求的是斜边还是直角边,以便合理选择是直接用勾股定理还是用勾股定理的变形公式 .
若求斜边,则直接用勾股定理;若求直角边,则用勾股定理的变形公式 .
感悟新知
知2-练
[ 中考·齐齐哈尔 ] 若直角三角形其中两条边的长分别为 3,4,则该直角三角形斜边上的高的长为 ________.
例3
解题秘方:紧扣“所给的较长边可能是直角边或斜边”进行分类解答 .
知2-练
感悟新知
解: 若直角三角形的两直角边长分别为 3,4,
则斜边长为 =5.
设直角三角形斜边上的高为 h,
则×3×4= ×5h,解得 h=2.4.
若直角三角形一条直角边长为 3,斜边长为 4,
则另一条直角边长为 = .
知2-练
感悟新知
答案:2.4 或
设直角三角形斜边上的高为 h1,
则×3× = ×4h1,解得 h1= .
综上所述,该直角三角形斜边上的高的长为 2.4 或.
知2-练
感悟新知
特别警示
当题中没有图或没有指明哪条边长是斜边长时,需要分类讨论,此题容易忽略4是斜边长的情况 .
知2-练
感悟新知
方法点拨
直接求直角三角形的边长时一般借助勾股定理求,但一定要分清楚直角边和斜边,若问题没有明确直角边和斜边,则要进行分类讨论 .
感悟新知
知3-讲
知识点
勾股定理的应用
3
1.勾股定理的应用范围:
勾股定理是直角三角形的一个重要性质,它把直角三角形有一个直角的“形”的特点转化为三边“数”的关系 . 利用勾股定理,可以解决与直角三角形有关的计算和证明问题,还可以解决生活、生产中的一些实际问题 .
感悟新知
知3-讲
2.勾股定理的应用的常见类型:
(1) 已知直角三角形的任意两边求第三边;
(2)已知直角三角形的任意一边确定另两边的关系;
(3)证明包含平方(算术平方根)关系的几何问题;
(4)求解几何体表面上的最短路程问题;
(5)构造方程(或方程组)计算有关线段长度, 解决生产、生活中的实际问题 .
知3-讲
感悟新知
特别提醒
运用勾股定理解决实际问题的一般步骤:
(1) 从实际问题中抽象出几何图形 .
(2) 确定要求的线段所在的直角三角形 .
(3) 找准直角边和斜边, 根据勾股定理建立等量关系并列出等式 .
(4)求得结果 .
知3-练
感悟新知
如图 1.2 - 3,在△ ABC 中,∠ C=90°, AC=2,点 D在 BC 上,∠ ADC=2 ∠ B, AD= ,则 BC 的长为 ________.
例4
解题秘方:紧扣三角形外角的性质及勾股定理解题 .
知3-练
感悟新知
答案: +1
解:∵∠ ADC=2 ∠ B,∠ ADC= ∠ B+ ∠ BAD,∴∠ B= ∠ BAD,
∴ BD=AD= .
∴在 Rt △ ACD 中, CD= =1,
∴ BC= +1.
知3-练
感悟新知
解法提醒
本题通过角的倍数关系得到边的相等关系,以及利用勾股定理求解 .
知3-练
感悟新知
[ 中考·南通 ] 如图 1.2 - 4,一艘轮船位于灯塔 P 的南偏东 60°方向,距离灯塔 P50 海里的 A 处,它沿正北方向航行一段时间后,到达位于灯塔 P的北偏东 45°方向上的 B 处,此时 B 处与灯塔 P的距离为 海里(结果保留根号) .
例5
知3-练
感悟新知
解: 如图 1.2 - 4,过点 P 作 PC ⊥ AB 于点 C.
在 Rt △ APC 中, AP=50 海里, ∠ APC=90° -60° =30°,∴ AC= AP=25 海里,
∴ PC= =25 (海里) .
解题秘方:将实际问题通过建模转化为直角三角形问题,然后利用勾股定理求解.
知3-练
感悟新知
答案:25
在 Rt △ PCB 中,∠ BPC=90° - 45° =45°,
∴∠ B=45° = ∠ BPC,∴ BC=PC=25 3海里,
∴ PB= =25 (海里) .
知3-练
感悟新知
方法点拨
求三角形的边或高时,可通过作辅助线构造直角三角形,用勾股定理来解决问题 .
感悟新知
知4-讲
知识点
勾股定理的逆定理
4
1. 勾股定理的逆定理: 如果三角形的三条边长 a, b, c 满足关系: a2+b2=c2 ,那么这个三角形是直角三角形 .
感悟新知
知4-讲
2. 利用边的关系判定直角三角形的步骤:
(1) “找”: 找出三角形三边中的最长边 .
(2)“算”: 计算较短两边的平方和与最长边的平方 .
(3)“判”: 若两者相等,则这个三角形是直角三角形;否则不是 .
感悟新知
知4-讲
3.勾股定理与其逆定理的关系:
定理 勾股定理 勾股定理的逆定理
区别 (1)勾股定理是以“一个三角
形是直角三角形”为条件,进
而得到这个直角三角形三边长
的关系,即 a2+b2=c2( c 为斜
边长);
(2)勾股定理是根据直角三角
形探求边的关系,体现了由形到数的转化 (1)勾股定理的逆定理是以“一个三角形的三边长a, b,c 满足 a2+b2=c2”为条件,进而得到这个三角形为直角三角形;
(2)勾股定理的逆定理是由三角形的三边关系探求三角形的形状,体现了由数到形的转化
感悟新知
知4-讲
联系 勾股定理与勾股定理的逆定理的条件和结论相反,勾股定理是直角三角形的性质,而其逆定理是直角三角形的判定,勾股定理及其逆定理都与直角三角形有关
知4-讲
感悟新知
特别提醒
◆勾股定理的逆定理是判定直角三角形的一个依据,在判定时不能说“在直角三角形中”“直角边”“斜边”,因为还没有确定是直角三角形 .
◆ a2+b2=c2 只 是 一 种表现形式,满足a2=b2+c2 或b2=a2+c2 的也是直角三角形,只是这时a或b为斜边 .
感悟新知
知4-练
判断满足下列条件的三角形是不是直角三角形:
(1)在△ ABC 中,∠ A=25° ,∠ C=65° ;
(2)在△ ABC 中, AC=12, AB=20, BC=16;
(3)一个三角形的三边长 a, b, c 满足 a∶ b∶ c=1∶1∶ 2 .
例6
知4-练
感悟新知
解题秘方:紧扣直角三角形的判定方法解题 .
解: (1)在△ ABC 中,
∵∠ A+ ∠ C=25° +65° =90°,
∴△ ABC 是直角三角形 .
知4-练
感悟新知
(2)在△ ABC 中,∵ AC2+BC2=122+162=202=AB2,
∴△ ABC 是直角三角形 .
(3)设 a=x,则 b=x, c= x.
∵ x2+x2= ( x ) 2,即 a2+b2=c2,
∴这个三角形是直角三角形 .
注意: 这个三角形也是
等腰三角形
知4-练
感悟新知
方法点拨
判断一个三角形是不是直角三角形的方法:
(1) 当已知条件与角度有关时,一般通过计算看 该三角形中是否有两 个角互余来判断;
(2)当已知条件与边有关时,一般通过计算 看 较 短两边的平方和是否等于最长边的平 方来判断 .
感悟新知
知5-讲
知识点
勾股数
5
1.勾股数: 满足 a2+b2=c2 的三个正整数称为勾股数 .
勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方 .
勾股数有无数组
感悟新知
知5-讲
2. 判别一组数是否为勾股数的一般步骤:
(1)“看”: 看是不是三个正整数;
(2)“找”: 找最大数;
(3)“算”: 计算最大数的平方与两个较小数的平方和;
(4)“判”: 若两者相等,则这三个数是一组勾股数;否则,不是一组勾股数 .
知5-讲
感悟新知
特别提醒
一组勾股数中的各数都乘相同的倍数可以得到一组新的勾股数:如3, 4, 5是勾股数,则6, 8, 10和9,12,15也是勾股数,即如果a, b, c是一组勾股数,那么na,nb, nc ( n 为正整数)也是一组勾股数 .
感悟新知
知5-练
下面四组数中是勾股数的一组是( )
A.6,7,8
B.5,8,13
C.1.5,2,2.5
D.21,28,35
例7
知5-练
感悟新知
答案:D
解题秘方:紧扣勾股数必须同时满足的两个条件进行判断 .
解:A.62+72 ≠ 82,故不是勾股数; B.52+82 ≠ 132,故不是勾股数; C.1.5 和 2.5 不是正整数,故不是勾股数; D.21,28,35 是正整数,且 212+282=352,故是勾股数.故选 D.
知5-练
感悟新知
方法点拨
确定勾股数的方法:
首先看这三个数是否是正整数, 然后看较小的两个数的平方和是否等于最大数的平方,记住常见的勾股数( 3,4, 5; 5, 12, 13; 8,15, 17; 7, 24, 25 )可以提高解题速度 .
直角三角形的性质和判定(Ⅱ)
三边平方关系
勾股定理的
逆定理
实际应用
几何应用
勾股定理
拼图法
面积法
验证
条件
结论
直角三角形
互逆定理
应用
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
