湘教版数学八年级下册 2.2.1 平行四边形的性质 导讲练课件 (共37张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 2.2.1 平行四边形的性质 导讲练课件 (共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
2.2 平行四边形
第二章 四边形
第1课时
平行四边形的性质
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
平行四边形
平行四边形的边、角性质
两条平行线之间的平行线段
平行四边形的对角线性质
知1-讲
感悟新知
知识点
平行四边形
1
1.定义 两组对边分别平行的四边形叫做平行四边形 .
平行四边形的定义既是它的一个性质,又是它的一种判定方法
感悟新知
知1-讲
特别提醒
平行四边形的定义有两个要素:
(1)是四边形;(2)两组对边分别平行.
作为四边形,平行四边形具有一般四边形的一切性质,如有四条边,四个内角,两条对角线,内角和为360°,外角和为360°等.
作为平行四边形,它区别于其他一般四边形的特殊性质为:平行四边形的两组对边分别平行 .
感悟新知
2. 表示方法: 平行四边形用符号“ ”表示,如图 2.2-1,平行四边形 ABCD 记作“ ABCD”,读作“平行四边形 ABCD” .
知1-讲
感悟新知
注意:
(1) 平行四边形的表示一定要按顺时针或逆时针依次注明各顶点,不能打乱顺序 .
(2) “ ”作为表示平行四边形的符号,不可单独使用它来代替“平行四边形” .
知1-讲
感悟新知
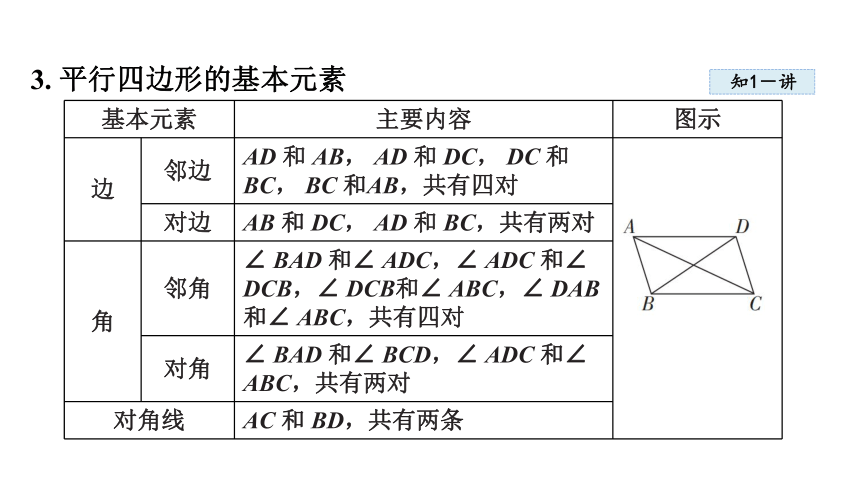
3. 平行四边形的基本元素
知1-讲
基本元素 主要内容 图示
边 邻边 AD 和 AB, AD 和 DC, DC 和 BC, BC 和AB,共有四对
对边 AB 和 DC, AD 和 BC,共有两对 角 邻角 ∠ BAD 和∠ ADC,∠ ADC 和∠ DCB,∠ DCB和∠ ABC,∠ DAB 和∠ ABC,共有四对 对角 ∠ BAD 和∠ BCD,∠ ADC 和∠ ABC,共有两对 对角线 AC 和 BD,共有两条
知1-练
感悟新知
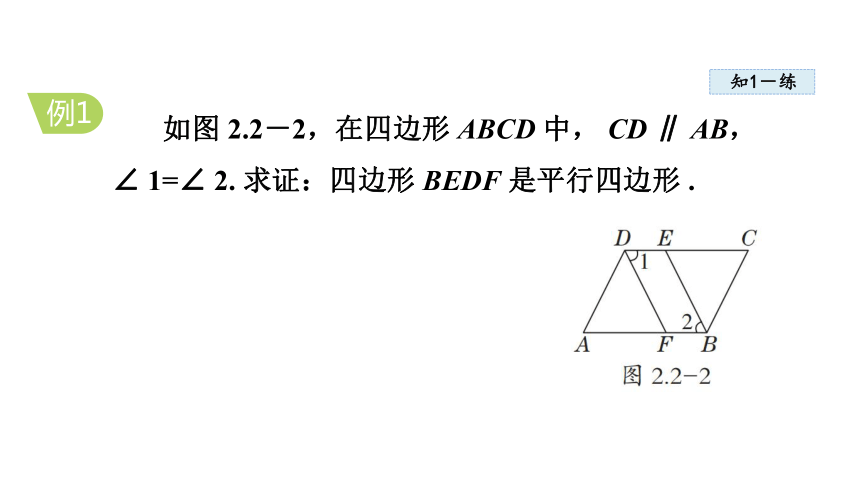
如图 2.2-2,在四边形 ABCD 中, CD ∥ AB, ∠ 1=∠ 2. 求证:四边形 BEDF 是平行四边形 .
例1
知1-练
感悟新知
解题秘方:紧扣平行四边形的定义(两组对边分别平行的四边形叫作平行四边形)进行证明 .
解法指导
要证一个四边形是平行四边形,可以通过证明它的两组对边分别平行来解决.
知1-练
感悟新知
证明: ∵ CD ∥ AB,∴∠ 1= ∠ DFA.
∵∠ 1= ∠ 2,∴∠ 2= ∠ DFA,
∴ DF ∥ BE,∴四边形 BEDF 是平行四边
形(两组对边分别平行的四边形是平行四边形) .
感悟新知
知2-讲
知识点
平行四边形的边、角性质
2
1.边的性质:平行四边形的对边平行;平行四边形的对边相等 .
数学语言: 如图 2.2-3,
∵四边形 ABCD 是平行四边形,
∴ AB ∥ CD, AD ∥ BC,AB=CD, AD=BC.
感悟新知
知2-讲
2.角的性质:
平行四边形的对角相等;平行四边形的邻角互补 .
数学语言: 如图 2.2-3,
∵四边形 ABCD 是平行四边形,
∴∠ A= ∠ C,∠ B= ∠ D,∠ A+ ∠ B=180°,
∠ B+ ∠ C=180°,∠ C+ ∠ D=180°,∠ A+ ∠ D=180° .
知2-讲
感悟新知
特别提醒
由于组成平行四边形的元素有边和角,因此讨论其性质也应从边和角这两个方面去看 .
(1)从边看:平行四边形 的对边平行且相等;
(2)从角看:平行四边形的对角相等、邻角互补 .
感悟新知
知2-练
如图 2.2-4,在 ABCD 中, AB=5 cm, BC=4 cm,∠ A=60° ,求 ABCD 的周长和∠ B, ∠ C 的度数 .
例2
知2-练
感悟新知
解题秘方:紧扣“平行四边形的边、角的性质”进行解答 .
知2-练
感悟新知
解: ∵平行四边形的对边相等,
∴ CD=AB=5 cm, AD=BC=4 cm.
∴ ABCD 的周长 =2( AB+BC) =2×(5+4) =18(cm) .
∵平行四边形的对角相等,∴∠ C= ∠ A=60°,
又∵平行四边形的邻角互补,
∴∠ B=180° - ∠ A=120° .
知2-练
感悟新知
方法点拨
根据平行四边形的对边相等可知平行四边形的周长等于相邻两边长的和的2倍.
感悟新知
知3-讲
知识点
两条平行线之间的平行线段
3
1.性质:夹在两条平行线间的平行线段相等 .
数学语言: 如图 2.2-5,直线 l1 ∥ l2, AB ∥CD,则 AB=CD.
知3-讲
感悟新知
特别提醒
1. 距离是指垂线段的长度,它是正值;
2. 当两条平 行线确定后,它们之间的距离是一定值, 不随位置的不同而改变 .
感悟新知
知3-讲
2. 拓展:(1)两条平行线中,一条直线上任意一点到另一条直线的距离叫作这两条平行线间的距离,平行线间的距离处处相等 .(2)等底等高的平行四边形的面积相等 .
知3-练
感悟新知
如 图 2.2 - 6, 直 线 a ∥ b, 点 A, E, F 在 直 线 a上, 点 B, C, D 在 直 线 b 上, BC=EF. △ ABC 与 △ DEF 的面积相等吗?为什么?
例3
知3-练
感悟新知
解题秘方:紧扣等底等高的三角形面积相等作三角形的高进行说明 .
知3-练
感悟新知
解法指导
◆由平行线间的距离处处相等,可知顶点都在两平行线上的三角形的高相等 .
◆解顶点在两平行线上的三角形的面积问题常作高(两平行线间的垂线段)进行解答.
知3-练
感悟新知
解: △ ABC 与△ DEF 的面积相等 . 理由如下:
如图 2.2 - 6,过点 A 作 AH1 ⊥直线 b,垂足为点 H1,
过点 D 作 DH2 ⊥直线 a,垂足为点 H2.
设△ ABC 和△ DEF 的面积分别为 S1 和 S2,
则 S1= BC· AH1, S2= EF· DH2.
∵直线 a ∥ b, AH1 ⊥直线 b, DH2 ⊥直线 a,
∴ AH1=DH2. 又∵ BC=EF,∴ S1=S2,
即△ ABC 与△ DEF 的面积相等 .
感悟新知
知4-讲
知识点
平行四边形的对角线性质
4
1.对角线的性质:平行四边形的对角线互相平分 .
数学语言:如图 2.2-7,
∵四边形 ABCD 是平行四边形,
∴ OA=OC= AC, OB=OD= BD.
感悟新知
知4-讲
2. 拓展:(1) 平行四边形的一条对角线将平行四边形分成面积相等的两部分,两条对角线将平行四边形分成面积相等的四部分 . (2) 若一条直线过平行四边形两条对角线的交点,则该直线平分平行四边形的周长和面积 .
知4-讲
感悟新知
图示
如图 2.2 - 8,
∵直线EF过平行四边形ABCD两条对角线的交点O,
∴ AE+AB+BF=FC+CD+DE= (AB+BC+CD+DA),
S 四边形 ABFE=S 四边形 FCDE= S ABCD.
感悟新知
知4-练
[ 期中·长沙 ] 如 图 2.2-9, ABCD 的周长为 80,△ BOC 的周长比△ AOB 的周长多 20,则 BC 的长为( )
A. 40 B. 10 C. 20 D. 30
例4
知4-练
感悟新知
解题秘方:紧扣平行四边形的对角线、边的性质进行解答 .
知4-练
感悟新知
解:由△ BOC 的周长比△ AOB 的周长
多 20,易知 BC-AB=20,①
∵ ABCD 的周长为 80,∴ BC+AB=40,②
① + ②,可得 2BC=60,∴ BC=30.
答案: D
知4-练
感悟新知
规律点拨
由“平行四边形的对角线互相平分”可以得出“平行四边形被它的两条对角线分成四个小三角形,相邻两个小三角形的周长之差等于平行四边形中对应的两邻边之差”.
感悟新知
知4-练
如图 2.2-10,在 ABCD 中,对角线 AC, BD 相交于点 O,过点 O 作直线 EF,分别交 AD, BC 于点 E, F. 四边形 ABFE 的面积与四边形 FCDE 的面积有何关系?并说明理由 .
例5
知4-练
感悟新知
解题秘方:紧扣平行四边形的对角线性质、全等三角形的性质进行解答 .
知4-练
感悟新知
解: S 四边形 ABFE=S 四边形 FCDE. 理由如下:
∵四边形 ABCD 是平行四边形,
∴ OA=OC, AD ∥ BC. ∴∠ 1= ∠ 2.
又∵∠ 3= ∠ 4,
∴△ AOE ≌△ COF. ∴ S △ AOE=S △ COF.
∵四边形 ABCD 是平行四边形,
∴ AB=CD, BC=DA,∠ ABC= ∠ CDA.
知4-练
感悟新知
∴△ ABC ≌△ CDA. ∴ S △ ABC=S △ CDA.
∵ S 四边形 ABFE=S △ ABC-S △ COF+S △ AOE=S △ ABC,
S 四边形 FCDE=S △ CDA-S △ AOE+S △ COF=S △ CDA,
∴ S 四边形 ABFE=S 四边形 FCDE.
知4-练
感悟新知
特别提醒
这是平行四边形对角线性质的两个拓展结论,即
(1)平行四边形的一条对角线将平行四边形分成两个面积相等的三角形 .
(2)过平行四边形的两条对角线交点的一条直线将平行四边形分成两个面积相等的梯形 .
本例的解答过程是对知识点中的两条拓展性质的部分结论的证明.
平行四边形的性质
平行四边形
定义
性质
表示方法
平行线间的距离
2.2 平行四边形
第二章 四边形
第1课时
平行四边形的性质
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
平行四边形
平行四边形的边、角性质
两条平行线之间的平行线段
平行四边形的对角线性质
知1-讲
感悟新知
知识点
平行四边形
1
1.定义 两组对边分别平行的四边形叫做平行四边形 .
平行四边形的定义既是它的一个性质,又是它的一种判定方法
感悟新知
知1-讲
特别提醒
平行四边形的定义有两个要素:
(1)是四边形;(2)两组对边分别平行.
作为四边形,平行四边形具有一般四边形的一切性质,如有四条边,四个内角,两条对角线,内角和为360°,外角和为360°等.
作为平行四边形,它区别于其他一般四边形的特殊性质为:平行四边形的两组对边分别平行 .
感悟新知
2. 表示方法: 平行四边形用符号“ ”表示,如图 2.2-1,平行四边形 ABCD 记作“ ABCD”,读作“平行四边形 ABCD” .
知1-讲
感悟新知
注意:
(1) 平行四边形的表示一定要按顺时针或逆时针依次注明各顶点,不能打乱顺序 .
(2) “ ”作为表示平行四边形的符号,不可单独使用它来代替“平行四边形” .
知1-讲
感悟新知
3. 平行四边形的基本元素
知1-讲
基本元素 主要内容 图示
边 邻边 AD 和 AB, AD 和 DC, DC 和 BC, BC 和AB,共有四对
对边 AB 和 DC, AD 和 BC,共有两对 角 邻角 ∠ BAD 和∠ ADC,∠ ADC 和∠ DCB,∠ DCB和∠ ABC,∠ DAB 和∠ ABC,共有四对 对角 ∠ BAD 和∠ BCD,∠ ADC 和∠ ABC,共有两对 对角线 AC 和 BD,共有两条
知1-练
感悟新知
如图 2.2-2,在四边形 ABCD 中, CD ∥ AB, ∠ 1=∠ 2. 求证:四边形 BEDF 是平行四边形 .
例1
知1-练
感悟新知
解题秘方:紧扣平行四边形的定义(两组对边分别平行的四边形叫作平行四边形)进行证明 .
解法指导
要证一个四边形是平行四边形,可以通过证明它的两组对边分别平行来解决.
知1-练
感悟新知
证明: ∵ CD ∥ AB,∴∠ 1= ∠ DFA.
∵∠ 1= ∠ 2,∴∠ 2= ∠ DFA,
∴ DF ∥ BE,∴四边形 BEDF 是平行四边
形(两组对边分别平行的四边形是平行四边形) .
感悟新知
知2-讲
知识点
平行四边形的边、角性质
2
1.边的性质:平行四边形的对边平行;平行四边形的对边相等 .
数学语言: 如图 2.2-3,
∵四边形 ABCD 是平行四边形,
∴ AB ∥ CD, AD ∥ BC,AB=CD, AD=BC.
感悟新知
知2-讲
2.角的性质:
平行四边形的对角相等;平行四边形的邻角互补 .
数学语言: 如图 2.2-3,
∵四边形 ABCD 是平行四边形,
∴∠ A= ∠ C,∠ B= ∠ D,∠ A+ ∠ B=180°,
∠ B+ ∠ C=180°,∠ C+ ∠ D=180°,∠ A+ ∠ D=180° .
知2-讲
感悟新知
特别提醒
由于组成平行四边形的元素有边和角,因此讨论其性质也应从边和角这两个方面去看 .
(1)从边看:平行四边形 的对边平行且相等;
(2)从角看:平行四边形的对角相等、邻角互补 .
感悟新知
知2-练
如图 2.2-4,在 ABCD 中, AB=5 cm, BC=4 cm,∠ A=60° ,求 ABCD 的周长和∠ B, ∠ C 的度数 .
例2
知2-练
感悟新知
解题秘方:紧扣“平行四边形的边、角的性质”进行解答 .
知2-练
感悟新知
解: ∵平行四边形的对边相等,
∴ CD=AB=5 cm, AD=BC=4 cm.
∴ ABCD 的周长 =2( AB+BC) =2×(5+4) =18(cm) .
∵平行四边形的对角相等,∴∠ C= ∠ A=60°,
又∵平行四边形的邻角互补,
∴∠ B=180° - ∠ A=120° .
知2-练
感悟新知
方法点拨
根据平行四边形的对边相等可知平行四边形的周长等于相邻两边长的和的2倍.
感悟新知
知3-讲
知识点
两条平行线之间的平行线段
3
1.性质:夹在两条平行线间的平行线段相等 .
数学语言: 如图 2.2-5,直线 l1 ∥ l2, AB ∥CD,则 AB=CD.
知3-讲
感悟新知
特别提醒
1. 距离是指垂线段的长度,它是正值;
2. 当两条平 行线确定后,它们之间的距离是一定值, 不随位置的不同而改变 .
感悟新知
知3-讲
2. 拓展:(1)两条平行线中,一条直线上任意一点到另一条直线的距离叫作这两条平行线间的距离,平行线间的距离处处相等 .(2)等底等高的平行四边形的面积相等 .
知3-练
感悟新知
如 图 2.2 - 6, 直 线 a ∥ b, 点 A, E, F 在 直 线 a上, 点 B, C, D 在 直 线 b 上, BC=EF. △ ABC 与 △ DEF 的面积相等吗?为什么?
例3
知3-练
感悟新知
解题秘方:紧扣等底等高的三角形面积相等作三角形的高进行说明 .
知3-练
感悟新知
解法指导
◆由平行线间的距离处处相等,可知顶点都在两平行线上的三角形的高相等 .
◆解顶点在两平行线上的三角形的面积问题常作高(两平行线间的垂线段)进行解答.
知3-练
感悟新知
解: △ ABC 与△ DEF 的面积相等 . 理由如下:
如图 2.2 - 6,过点 A 作 AH1 ⊥直线 b,垂足为点 H1,
过点 D 作 DH2 ⊥直线 a,垂足为点 H2.
设△ ABC 和△ DEF 的面积分别为 S1 和 S2,
则 S1= BC· AH1, S2= EF· DH2.
∵直线 a ∥ b, AH1 ⊥直线 b, DH2 ⊥直线 a,
∴ AH1=DH2. 又∵ BC=EF,∴ S1=S2,
即△ ABC 与△ DEF 的面积相等 .
感悟新知
知4-讲
知识点
平行四边形的对角线性质
4
1.对角线的性质:平行四边形的对角线互相平分 .
数学语言:如图 2.2-7,
∵四边形 ABCD 是平行四边形,
∴ OA=OC= AC, OB=OD= BD.
感悟新知
知4-讲
2. 拓展:(1) 平行四边形的一条对角线将平行四边形分成面积相等的两部分,两条对角线将平行四边形分成面积相等的四部分 . (2) 若一条直线过平行四边形两条对角线的交点,则该直线平分平行四边形的周长和面积 .
知4-讲
感悟新知
图示
如图 2.2 - 8,
∵直线EF过平行四边形ABCD两条对角线的交点O,
∴ AE+AB+BF=FC+CD+DE= (AB+BC+CD+DA),
S 四边形 ABFE=S 四边形 FCDE= S ABCD.
感悟新知
知4-练
[ 期中·长沙 ] 如 图 2.2-9, ABCD 的周长为 80,△ BOC 的周长比△ AOB 的周长多 20,则 BC 的长为( )
A. 40 B. 10 C. 20 D. 30
例4
知4-练
感悟新知
解题秘方:紧扣平行四边形的对角线、边的性质进行解答 .
知4-练
感悟新知
解:由△ BOC 的周长比△ AOB 的周长
多 20,易知 BC-AB=20,①
∵ ABCD 的周长为 80,∴ BC+AB=40,②
① + ②,可得 2BC=60,∴ BC=30.
答案: D
知4-练
感悟新知
规律点拨
由“平行四边形的对角线互相平分”可以得出“平行四边形被它的两条对角线分成四个小三角形,相邻两个小三角形的周长之差等于平行四边形中对应的两邻边之差”.
感悟新知
知4-练
如图 2.2-10,在 ABCD 中,对角线 AC, BD 相交于点 O,过点 O 作直线 EF,分别交 AD, BC 于点 E, F. 四边形 ABFE 的面积与四边形 FCDE 的面积有何关系?并说明理由 .
例5
知4-练
感悟新知
解题秘方:紧扣平行四边形的对角线性质、全等三角形的性质进行解答 .
知4-练
感悟新知
解: S 四边形 ABFE=S 四边形 FCDE. 理由如下:
∵四边形 ABCD 是平行四边形,
∴ OA=OC, AD ∥ BC. ∴∠ 1= ∠ 2.
又∵∠ 3= ∠ 4,
∴△ AOE ≌△ COF. ∴ S △ AOE=S △ COF.
∵四边形 ABCD 是平行四边形,
∴ AB=CD, BC=DA,∠ ABC= ∠ CDA.
知4-练
感悟新知
∴△ ABC ≌△ CDA. ∴ S △ ABC=S △ CDA.
∵ S 四边形 ABFE=S △ ABC-S △ COF+S △ AOE=S △ ABC,
S 四边形 FCDE=S △ CDA-S △ AOE+S △ COF=S △ CDA,
∴ S 四边形 ABFE=S 四边形 FCDE.
知4-练
感悟新知
特别提醒
这是平行四边形对角线性质的两个拓展结论,即
(1)平行四边形的一条对角线将平行四边形分成两个面积相等的三角形 .
(2)过平行四边形的两条对角线交点的一条直线将平行四边形分成两个面积相等的梯形 .
本例的解答过程是对知识点中的两条拓展性质的部分结论的证明.
平行四边形的性质
平行四边形
定义
性质
表示方法
平行线间的距离
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
