湘教版数学八年级下册 2.6 菱形 导讲练课件(共29张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 2.6 菱形 导讲练课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
2.6 菱形
第二章 四边形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
菱形的定义及其性质
菱形的判定
知1-讲
感悟新知
知识点
菱形的定义及其性质
1
1.定义:一组邻边相等的平行四边形叫做菱形 .
特别提醒
菱形必须满足两个条件:一是平行四边形;二是一组邻边相等.二者必须同时具备,缺一不可 .
感悟新知
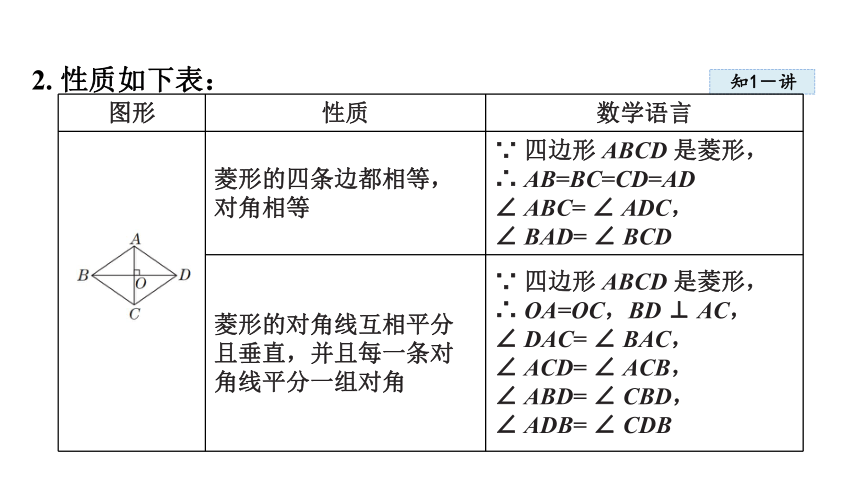
2. 性质如下表:
知1-讲
图形 性质 数学语言
菱形的四条边都相等,对角相等 ∵ 四边形 ABCD 是菱形,
∴ AB=BC=CD=AD
∠ ABC= ∠ ADC,
∠ BAD= ∠ BCD
菱形的对角线互相平分且垂直,并且每一条对角线平分一组对角 ∵ 四边形 ABCD 是菱形,
∴ OA=OC,BD ⊥ AC,
∠ DAC= ∠ BAC,
∠ ACD= ∠ ACB,
∠ ABD= ∠ CBD,
∠ ADB= ∠ CDB
感悟新知
知1-讲
图形 性质 数学语言
菱形是中心对称图形,对角线的交点是它的对称中心.菱形是轴对称图形,两条对角线所在直线都是它的对称轴 感悟新知
3. (1) 菱形的面积 = 底 × 高 = 两条对角线长乘积的一半 .
(2)菱形的两条对角线把菱形分成四个全等的直角三角形.
知1-讲
知1-练
感悟新知
[ 中考·鞍山 ] 如图 2.6 - 1,在 ABCD 中, G 为 BC 边上一点, DG=DC,延长 DG 交 AB 的延长线于点 E,过点 A 作AF ∥ ED 交 CD 的延长线于点 F. 求证:四边形 AEDF 是菱形 .
例1
知1-练
感悟新知
方法点拨
菱形的定义既是菱形的性质,也是菱形的一种判定方法 .
知1-练
感悟新知
解题秘方:紧扣定义中的“两个条件”进行判断 .
知1-练
感悟新知
证明: ∵四边形 ABCD 是平行四边形,
∴∠ BAD= ∠ C, AD ∥ BC, AB ∥ CD.
∵ AF ∥ ED,∴四边形 AEDF 是平行四边形 .
∵ AD ∥ BC,∴∠ DGC= ∠ ADE.
∵ DG=DC,∴∠ DGC= ∠ C,∴∠ C= ∠ ADE,
∴∠ BAD= ∠ ADE,∴ AE=DE,
∴平行四边形 AEDF 是菱形 .
知1-练
感悟新知
特别提醒
在用菱形的定义判定一个四边形是菱形时,首先判定这个四边形是平行四边形,再证一组邻边相等 .
知1-练
感悟新知
[ 中考·长沙 ] 如图 2.6 - 2,菱形 ABCD 的对角线 AC,BD 相交于点 O,点 E 是边 AB 的中点,若 OE=6,则 BC 的长为 ________.
例2
知1-练
感悟新知
方法点拨
当题目中出现一条边的中点时,往往需要用到直角三角形斜边上的中线的性质;当题目中出现了两条边的中点时,往往需要用到三角形的中位线定理 .
知1-练
感悟新知
解:∵四边形 ABCD 是菱形,∴ OA=OC.
∵点 E 是边 AB 的中点,∴ OE 是△ ABC 的中位线,
∴ BC=2OE=2×6=12.
解题秘方:先根据菱形的性质可得 OA=OC,再根据三角形的中位线定理即可得解 .
答案: 12
知1-练
感悟新知
[ 中考·黔东南州 ] 如图 2.6-3, BD 是菱形 ABCD 的一条对角线,点 E 在 BC 的延长线上,若∠ ADB=32°,则∠ DCE的度数为 _______° .
例3
解题秘方:紧扣菱形的性质、三角形外角的性质求解 .
知1-练
感悟新知
技巧点拨
利用菱形的性质得到线段平行、两角相等,再利用平行线的性质与三角形外角的性质求得结果 .
知1-练
感悟新知
解: ∵菱形 ABCD 是轴对称图形,∠ ADB=32°,
∴∠ CDB= ∠ ADB=32°, AD ∥ BC,
∴∠ DBC= ∠ ADB=32°,
∴∠ DCE = ∠ DBC+ ∠ CDB=32° +32° =64°.
答案: 64
感悟新知
知2-讲
知识点
菱形的判定
2
1. 判定定理 1: 四边都相等的四边形是菱形 .
数学语言: 如图2.6 - 4,
在四边形 ABCD 中,
∵ AB=BC=CD=DA,
∴四边形 ABCD 是菱形 .
感悟新知
知2-讲
2. 判定定理 2:对角线互相垂直的平行四边形是菱形 .
数学语言:
如图 2.6 - 4,在 ABCD 中,
∵ AC ⊥ BD,
∴ ABCD 是菱形 .
知2-讲
感悟新知
特别提醒
1. 菱形的判定定理和性质定理是互逆定理 .
2. 判定菱形的常见思路
四边形
平行四边形
可依据题目特点选取不同的方法 .
感悟新知
知2-练
[ 中考·襄阳 ] 如图 2.6-5, BD 为 ABCD 的对角线 .
例4
解题秘方: (1)按照垂直平分线的作法作图即可; (2)证明△ DEO ≌△ BFO,得到 DE=BF,根据垂直平分线的性质证四边相等即可 .
知2-练
感悟新知
技巧点拨
判定菱形的方法:
(1)若用边进行判定:
先证明四边形是平行四边形,再证明一组邻边相等,或直接证明四边形的四条边都相等;
(2)若用对角线进行判定:先证明四边形是平行四边形,再证明对角线互相垂直,或直接证明四边形的对角线互相垂直平分.
知2-练
感悟新知
解: 如图 2.6-6,直线 EF 即为所求 .
(1)作对角线 BD 的垂直平分线,分别交 AD, BC, BD于点 E, F, O(尺规作图,不写作法,保留作图痕迹);
知2-练
感悟新知
证明: ∵ EF 垂直平分 BD,
∴ DO=BO, BE=DE, BF=DF.
∵四边形 ABCD 是平行四边形,∴ AD ∥ BC,
∴∠ DEO= ∠ BFO,∠ EDO= ∠ FBO,
∴△ DEO ≌△ BFO(AAS),
∴ DE=BF,∴ BE=DE=BF=DF,
∴四边形 BEDF 是菱形.
(2)连接 BE, DF.求证:四边形 BEDF 为菱形 .
感悟新知
知2-练
如图 2.6-7,已知△ ABC, D 是 AC 的中点, DE ⊥AC 于点 D,交 AB 于点 E,过点 C 作 CF ∥ BA 交 ED 的延长线于点 F,连接 CE, AF. 求证:四边形 AECF 是菱形 .
例5
知2-练
感悟新知
解题秘方:紧扣对角线互相垂直这一条件,从判定平行四边形入手 .
知2-练
感悟新知
方法点拨
证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要考虑证明这个四边形是平行四边形,用“对角线互相垂直的平行四边形是菱形”进行证明 .
知2-练
感悟新知
证明: ∵ CF ∥ BA,∴∠ EAD= ∠ FCD,
∠ AED= ∠ CFD.
又∵ D 是 AC 的中点,∴ AD=CD,
∴△ ADE ≌△ CDF(AAS),∴ AE=CF.
又∵ AE ∥ CF,∴四边形 AECF 是平行四边形 .
又∵ DE ⊥ AC,∴四边形 AECF 是菱形 .
菱形
轴对称性
边的关系
菱形
性质
判定
定义
对角线的关系
边的性质
对角线的性质
角的性质
2.6 菱形
第二章 四边形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
菱形的定义及其性质
菱形的判定
知1-讲
感悟新知
知识点
菱形的定义及其性质
1
1.定义:一组邻边相等的平行四边形叫做菱形 .
特别提醒
菱形必须满足两个条件:一是平行四边形;二是一组邻边相等.二者必须同时具备,缺一不可 .
感悟新知
2. 性质如下表:
知1-讲
图形 性质 数学语言
菱形的四条边都相等,对角相等 ∵ 四边形 ABCD 是菱形,
∴ AB=BC=CD=AD
∠ ABC= ∠ ADC,
∠ BAD= ∠ BCD
菱形的对角线互相平分且垂直,并且每一条对角线平分一组对角 ∵ 四边形 ABCD 是菱形,
∴ OA=OC,BD ⊥ AC,
∠ DAC= ∠ BAC,
∠ ACD= ∠ ACB,
∠ ABD= ∠ CBD,
∠ ADB= ∠ CDB
感悟新知
知1-讲
图形 性质 数学语言
菱形是中心对称图形,对角线的交点是它的对称中心.菱形是轴对称图形,两条对角线所在直线都是它的对称轴 感悟新知
3. (1) 菱形的面积 = 底 × 高 = 两条对角线长乘积的一半 .
(2)菱形的两条对角线把菱形分成四个全等的直角三角形.
知1-讲
知1-练
感悟新知
[ 中考·鞍山 ] 如图 2.6 - 1,在 ABCD 中, G 为 BC 边上一点, DG=DC,延长 DG 交 AB 的延长线于点 E,过点 A 作AF ∥ ED 交 CD 的延长线于点 F. 求证:四边形 AEDF 是菱形 .
例1
知1-练
感悟新知
方法点拨
菱形的定义既是菱形的性质,也是菱形的一种判定方法 .
知1-练
感悟新知
解题秘方:紧扣定义中的“两个条件”进行判断 .
知1-练
感悟新知
证明: ∵四边形 ABCD 是平行四边形,
∴∠ BAD= ∠ C, AD ∥ BC, AB ∥ CD.
∵ AF ∥ ED,∴四边形 AEDF 是平行四边形 .
∵ AD ∥ BC,∴∠ DGC= ∠ ADE.
∵ DG=DC,∴∠ DGC= ∠ C,∴∠ C= ∠ ADE,
∴∠ BAD= ∠ ADE,∴ AE=DE,
∴平行四边形 AEDF 是菱形 .
知1-练
感悟新知
特别提醒
在用菱形的定义判定一个四边形是菱形时,首先判定这个四边形是平行四边形,再证一组邻边相等 .
知1-练
感悟新知
[ 中考·长沙 ] 如图 2.6 - 2,菱形 ABCD 的对角线 AC,BD 相交于点 O,点 E 是边 AB 的中点,若 OE=6,则 BC 的长为 ________.
例2
知1-练
感悟新知
方法点拨
当题目中出现一条边的中点时,往往需要用到直角三角形斜边上的中线的性质;当题目中出现了两条边的中点时,往往需要用到三角形的中位线定理 .
知1-练
感悟新知
解:∵四边形 ABCD 是菱形,∴ OA=OC.
∵点 E 是边 AB 的中点,∴ OE 是△ ABC 的中位线,
∴ BC=2OE=2×6=12.
解题秘方:先根据菱形的性质可得 OA=OC,再根据三角形的中位线定理即可得解 .
答案: 12
知1-练
感悟新知
[ 中考·黔东南州 ] 如图 2.6-3, BD 是菱形 ABCD 的一条对角线,点 E 在 BC 的延长线上,若∠ ADB=32°,则∠ DCE的度数为 _______° .
例3
解题秘方:紧扣菱形的性质、三角形外角的性质求解 .
知1-练
感悟新知
技巧点拨
利用菱形的性质得到线段平行、两角相等,再利用平行线的性质与三角形外角的性质求得结果 .
知1-练
感悟新知
解: ∵菱形 ABCD 是轴对称图形,∠ ADB=32°,
∴∠ CDB= ∠ ADB=32°, AD ∥ BC,
∴∠ DBC= ∠ ADB=32°,
∴∠ DCE = ∠ DBC+ ∠ CDB=32° +32° =64°.
答案: 64
感悟新知
知2-讲
知识点
菱形的判定
2
1. 判定定理 1: 四边都相等的四边形是菱形 .
数学语言: 如图2.6 - 4,
在四边形 ABCD 中,
∵ AB=BC=CD=DA,
∴四边形 ABCD 是菱形 .
感悟新知
知2-讲
2. 判定定理 2:对角线互相垂直的平行四边形是菱形 .
数学语言:
如图 2.6 - 4,在 ABCD 中,
∵ AC ⊥ BD,
∴ ABCD 是菱形 .
知2-讲
感悟新知
特别提醒
1. 菱形的判定定理和性质定理是互逆定理 .
2. 判定菱形的常见思路
四边形
平行四边形
可依据题目特点选取不同的方法 .
感悟新知
知2-练
[ 中考·襄阳 ] 如图 2.6-5, BD 为 ABCD 的对角线 .
例4
解题秘方: (1)按照垂直平分线的作法作图即可; (2)证明△ DEO ≌△ BFO,得到 DE=BF,根据垂直平分线的性质证四边相等即可 .
知2-练
感悟新知
技巧点拨
判定菱形的方法:
(1)若用边进行判定:
先证明四边形是平行四边形,再证明一组邻边相等,或直接证明四边形的四条边都相等;
(2)若用对角线进行判定:先证明四边形是平行四边形,再证明对角线互相垂直,或直接证明四边形的对角线互相垂直平分.
知2-练
感悟新知
解: 如图 2.6-6,直线 EF 即为所求 .
(1)作对角线 BD 的垂直平分线,分别交 AD, BC, BD于点 E, F, O(尺规作图,不写作法,保留作图痕迹);
知2-练
感悟新知
证明: ∵ EF 垂直平分 BD,
∴ DO=BO, BE=DE, BF=DF.
∵四边形 ABCD 是平行四边形,∴ AD ∥ BC,
∴∠ DEO= ∠ BFO,∠ EDO= ∠ FBO,
∴△ DEO ≌△ BFO(AAS),
∴ DE=BF,∴ BE=DE=BF=DF,
∴四边形 BEDF 是菱形.
(2)连接 BE, DF.求证:四边形 BEDF 为菱形 .
感悟新知
知2-练
如图 2.6-7,已知△ ABC, D 是 AC 的中点, DE ⊥AC 于点 D,交 AB 于点 E,过点 C 作 CF ∥ BA 交 ED 的延长线于点 F,连接 CE, AF. 求证:四边形 AECF 是菱形 .
例5
知2-练
感悟新知
解题秘方:紧扣对角线互相垂直这一条件,从判定平行四边形入手 .
知2-练
感悟新知
方法点拨
证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要考虑证明这个四边形是平行四边形,用“对角线互相垂直的平行四边形是菱形”进行证明 .
知2-练
感悟新知
证明: ∵ CF ∥ BA,∴∠ EAD= ∠ FCD,
∠ AED= ∠ CFD.
又∵ D 是 AC 的中点,∴ AD=CD,
∴△ ADE ≌△ CDF(AAS),∴ AE=CF.
又∵ AE ∥ CF,∴四边形 AECF 是平行四边形 .
又∵ DE ⊥ AC,∴四边形 AECF 是菱形 .
菱形
轴对称性
边的关系
菱形
性质
判定
定义
对角线的关系
边的性质
对角线的性质
角的性质
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
