湘教版数学八年级下册 2.5 矩形 导讲练课件(共33张PPT)
文档属性
| 名称 | 湘教版数学八年级下册 2.5 矩形 导讲练课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 22:29:30 | ||
图片预览









文档简介
(共33张PPT)
2.5 矩形
第二章 四边形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
矩形的定义及其性质
矩形的判定
知1-讲
感悟新知
知识点
矩形的定义及其性质
1
1.定义:有一个角是直角的平行四边形叫做矩形 .
感悟新知
知1-讲
特别提醒
1.矩形必须具备两个条件:
(1) 它是一个平行四边形;
(2) 它有一个角是直角 . 这两个条件缺一不可 .
2. 由矩形的定义知,矩形一定是平行四边形,但平行四边形不一定是矩形.矩形的定义可以作为判定一个四边形是矩形的一种方法 .
感悟新知
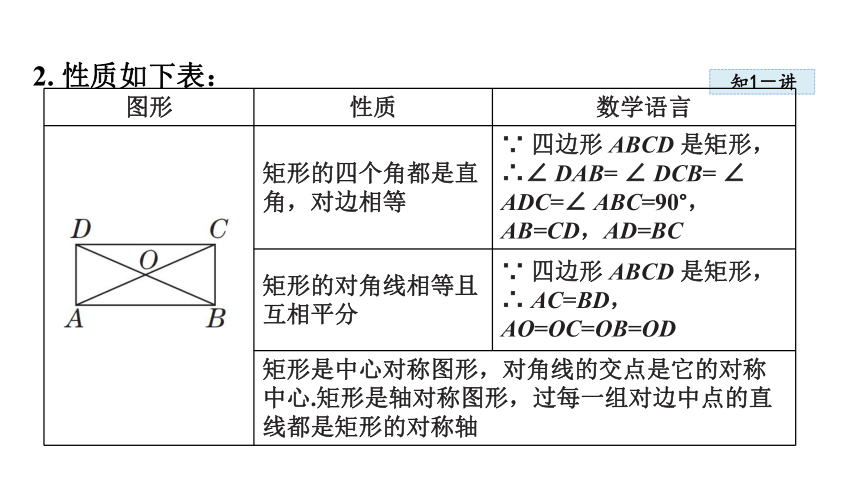
2. 性质如下表:
知1-讲
图形 性质 数学语言
矩形的四个角都是直角,对边相等 ∵ 四边形 ABCD 是矩形,
∴∠ DAB= ∠ DCB= ∠ ADC=∠ ABC=90°,AB=CD,AD=BC
矩形的对角线相等且互相平分 ∵ 四边形 ABCD 是矩形,
∴ AC=BD, AO=OC=OB=OD
矩形是中心对称图形,对角线的交点是它的对称中心.矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴 感悟新知
特别提醒: 矩形的一条对角线把矩形分成两个全等的直角三角形,矩形的两条对角线将矩形分成两对全等的等腰三角形,分成四个面积相等的等腰三角形,因此有关矩形的计算问题经常通常转化到直角三角形和等腰三角形中来解决 .
知1-讲
知1-练
感悟新知
如图 2.5-1,在 ABCD 中,点 E, F 分别为 BC 边上的点,且 BE=CF, AF=DE,求证: ABCD是矩形 .
例1
知1-练
感悟新知
解题秘方:紧扣矩形定义的“两个条件”进行证明 .
知1-练
感悟新知
证明: ∵四边形 ABCD 是平行四边形,
∴ AB=CD,∠ B+ ∠ C = 180° .
∵ BE=CF,∴ BE+EF=CF+EF,即 BF=CE.
又∵ AF=DE,∴△ ABF ≌△ DCE.
∴∠ B= ∠ C=90° . ∴ ABCD 是矩形 .
知1-练
感悟新知
方法点拨
由定义来判定矩形,要在平行四边形的前提下,判定有一个角是90°,若在四边形的前提下,则需先证平行四边形,再判定有一个角是90°,矩形的定义既是矩形的性质也是矩形的判定.
知1-练
感悟新知
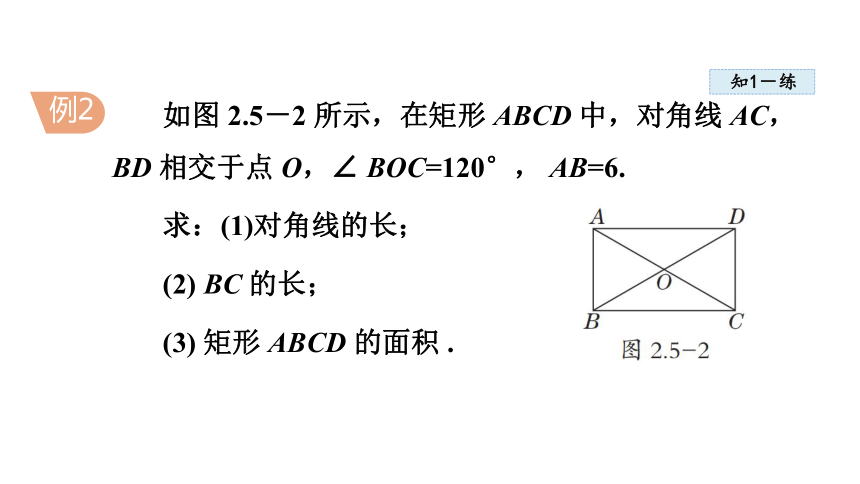
如图 2.5-2 所示,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,∠ BOC=120°, AB=6.
求:(1)对角线的长;
(2) BC 的长;
(3) 矩形 ABCD 的面积 .
例2
知1-练
感悟新知
解题秘方:紧扣矩形的“角、对角线的性质”进行计算 .
知1-练
感悟新知
方法点拨
1. 有一个角是60°的等腰三角形是等边三角形.
2.矩形的两条对角线把矩形分成四个等腰三角形;另外,矩形的对角线与两邻边构成四个直角三角形,矩形中的有关计算通常需要用到等腰三角形的性质或直角三角形的有关知识来解决 .
知1-练
感悟新知
解: (1)∵四边形 ABCD 是矩形,
∴ AC=BD, OA=OC=OB=OD.
又∵∠ BOC=120°,∴∠ AOB=60°,
∴△ AOB 是等边三角形,
∴ OA=AB=6,∴ BD=AC=2OA=2×6=12.
知1-练
感悟新知
(2)∵四边形 ABCD 是矩形,
∴∠ ABC=90° .
∴ BC= = =6 .
(3) S 矩形 ABCD=AB· BC=6×6 =36 .
知1-练
感悟新知
如图 2.5-3,直线 EF 过矩形 ABCD 对角线的交点 O,分别交 AB, CD 于点 E, F,若 AB=3, BC=4,则 S 阴影 =____.
例3
知1-练
感悟新知
解题秘方:紧扣矩形的中心对称性,将阴影部分转化到一起计算 .
知1-练
感悟新知
解: ∵四边形 ABCD 是矩形,∴ OB=OD, AB ∥ CD,∴∠ EBO= ∠ FDO.
又∵∠ EOB=∠ FOD,∴△ OEB ≌△ OFD,
∴ S 阴影 =S △ ABO= S 矩形 ABCD= ×3×4=3.
答案: 3
知1-练
感悟新知
方法点拨
矩形既是轴对称图形又是中心对称图形,根据对称性将阴影部分的面积转化为规则的几何图形的面积求解.体现了转化思想 .
感悟新知
知2-讲
知识点
矩形的判定
2
1. 判定定理 1: 三个角是直角的四边形是矩形 .
数学语言: 如图 2.5 - 4,在四边形 ABCD 中,
∵∠ A= ∠ B= ∠ C=90°,∴四边形 ABCD 是矩形 .
感悟新知
知2-讲
2. 判定定理 2: 对角线相等的平行四边形是矩形 .
数学语言: 如图 2.5 - 5,在 ABCD 中,∵ AC=BD,
∴四边形 ABCD 是矩形 .
注意: 矩形的判定和性质互为逆定理 .
知2-讲
感悟新知
特别提醒
矩形判定的常见思路:
从角上证明:
(1)四边形矩形;
(2)平行四边形矩形.
从对角线上证明:
(1)平行四边形矩形;
(2)四边形 矩形 .
知2-练
感悟新知
如图 2.5-6, 在四边形 ABCD 中, ∠ A= ∠ BCD=90°,BC=CD, CE ⊥ AD,垂足为 E,求证: AE=CE.
例4
知2-练
感悟新知
解题秘方:观察几何图形可知,无法用全等三角形等知识直接证明 AE=CE,因此可选择过点 B 作一条垂线段,同时构造一个矩形和一对全等三角形,借助中间量间接证得两条线段相等 .
知2-练
感悟新知
证明: 如图 2.5-6,过点 B 作 BF ⊥ CE 于点 F.
∵ CE ⊥ AD,∴∠ D+ ∠ DCE=90° .
∵∠ BCD=90°,∴∠ BCF+ ∠ DCE=90°,
∴∠ BCF= ∠ D.
在△ BCF 和△ CDE 中,
知2-练
感悟新知
∴△ BCF ≌△ CDE( AAS),∴ BF=CE.
∵ CE ⊥ AD, BF ⊥ CE,∴∠ AEF=90°,∠ BFE=90° .
又∵∠ A=90°,∴四边形 AEFB 是矩形,
∴ AE=BF,∴ AE=CE.
知2-练
感悟新知
方法点拨
本题通过作垂线段,利用“AAS”得到△BCF≌△CDE,再利用“有三个角是直角的四边形是矩形”得到四边形AEFB是矩形,最后根据全等三角形和矩形的性质得到线段相等 .
知2-练
感悟新知
[ 中考·长沙 ]如图 2.5-7, ABCD 的对角线 AC, BD相交于点 O,△ OAB 是等边三角形, AB=4.
(1)求证: ABCD 是矩形;
(2)求 AD 的长 .
例5
知2-练
感悟新知
解题秘方:紧扣“平行四边形”这一前提,从“对角线相等” 入手(或有一个角是直角入手)进行证明 .
知2-练
感悟新知
(1)证明: ∵四边形 ABCD 是平行四边形,
∴ 2OA=AC,2OB=BD.
∵△ OAB 是等边三角形,
∴ OA=OB,∴ AC=BD,∴ ABCD 是矩形 .
知2-练
感悟新知
(2)解: ∵△ OAB 是等边三角形, AB=4,
∴ OB=AB=4,∴ BD=2OB=8.
∵ ABCD 是矩形,∴∠ BAD=90°,
∴在 Rt △ ABD 中, AD= = =4 .
知2-练
感悟新知
方法点拨
证明一个平行四边形为矩形的两种方法:一种是证明有一个角是直角;另一种是证明两条对角线相等 .
矩形
矩形
性质
判定
定义
角的关系
对角线的关系
边的性质
角的性质
对角线的性质
2.5 矩形
第二章 四边形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
矩形的定义及其性质
矩形的判定
知1-讲
感悟新知
知识点
矩形的定义及其性质
1
1.定义:有一个角是直角的平行四边形叫做矩形 .
感悟新知
知1-讲
特别提醒
1.矩形必须具备两个条件:
(1) 它是一个平行四边形;
(2) 它有一个角是直角 . 这两个条件缺一不可 .
2. 由矩形的定义知,矩形一定是平行四边形,但平行四边形不一定是矩形.矩形的定义可以作为判定一个四边形是矩形的一种方法 .
感悟新知
2. 性质如下表:
知1-讲
图形 性质 数学语言
矩形的四个角都是直角,对边相等 ∵ 四边形 ABCD 是矩形,
∴∠ DAB= ∠ DCB= ∠ ADC=∠ ABC=90°,AB=CD,AD=BC
矩形的对角线相等且互相平分 ∵ 四边形 ABCD 是矩形,
∴ AC=BD, AO=OC=OB=OD
矩形是中心对称图形,对角线的交点是它的对称中心.矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴 感悟新知
特别提醒: 矩形的一条对角线把矩形分成两个全等的直角三角形,矩形的两条对角线将矩形分成两对全等的等腰三角形,分成四个面积相等的等腰三角形,因此有关矩形的计算问题经常通常转化到直角三角形和等腰三角形中来解决 .
知1-讲
知1-练
感悟新知
如图 2.5-1,在 ABCD 中,点 E, F 分别为 BC 边上的点,且 BE=CF, AF=DE,求证: ABCD是矩形 .
例1
知1-练
感悟新知
解题秘方:紧扣矩形定义的“两个条件”进行证明 .
知1-练
感悟新知
证明: ∵四边形 ABCD 是平行四边形,
∴ AB=CD,∠ B+ ∠ C = 180° .
∵ BE=CF,∴ BE+EF=CF+EF,即 BF=CE.
又∵ AF=DE,∴△ ABF ≌△ DCE.
∴∠ B= ∠ C=90° . ∴ ABCD 是矩形 .
知1-练
感悟新知
方法点拨
由定义来判定矩形,要在平行四边形的前提下,判定有一个角是90°,若在四边形的前提下,则需先证平行四边形,再判定有一个角是90°,矩形的定义既是矩形的性质也是矩形的判定.
知1-练
感悟新知
如图 2.5-2 所示,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,∠ BOC=120°, AB=6.
求:(1)对角线的长;
(2) BC 的长;
(3) 矩形 ABCD 的面积 .
例2
知1-练
感悟新知
解题秘方:紧扣矩形的“角、对角线的性质”进行计算 .
知1-练
感悟新知
方法点拨
1. 有一个角是60°的等腰三角形是等边三角形.
2.矩形的两条对角线把矩形分成四个等腰三角形;另外,矩形的对角线与两邻边构成四个直角三角形,矩形中的有关计算通常需要用到等腰三角形的性质或直角三角形的有关知识来解决 .
知1-练
感悟新知
解: (1)∵四边形 ABCD 是矩形,
∴ AC=BD, OA=OC=OB=OD.
又∵∠ BOC=120°,∴∠ AOB=60°,
∴△ AOB 是等边三角形,
∴ OA=AB=6,∴ BD=AC=2OA=2×6=12.
知1-练
感悟新知
(2)∵四边形 ABCD 是矩形,
∴∠ ABC=90° .
∴ BC= = =6 .
(3) S 矩形 ABCD=AB· BC=6×6 =36 .
知1-练
感悟新知
如图 2.5-3,直线 EF 过矩形 ABCD 对角线的交点 O,分别交 AB, CD 于点 E, F,若 AB=3, BC=4,则 S 阴影 =____.
例3
知1-练
感悟新知
解题秘方:紧扣矩形的中心对称性,将阴影部分转化到一起计算 .
知1-练
感悟新知
解: ∵四边形 ABCD 是矩形,∴ OB=OD, AB ∥ CD,∴∠ EBO= ∠ FDO.
又∵∠ EOB=∠ FOD,∴△ OEB ≌△ OFD,
∴ S 阴影 =S △ ABO= S 矩形 ABCD= ×3×4=3.
答案: 3
知1-练
感悟新知
方法点拨
矩形既是轴对称图形又是中心对称图形,根据对称性将阴影部分的面积转化为规则的几何图形的面积求解.体现了转化思想 .
感悟新知
知2-讲
知识点
矩形的判定
2
1. 判定定理 1: 三个角是直角的四边形是矩形 .
数学语言: 如图 2.5 - 4,在四边形 ABCD 中,
∵∠ A= ∠ B= ∠ C=90°,∴四边形 ABCD 是矩形 .
感悟新知
知2-讲
2. 判定定理 2: 对角线相等的平行四边形是矩形 .
数学语言: 如图 2.5 - 5,在 ABCD 中,∵ AC=BD,
∴四边形 ABCD 是矩形 .
注意: 矩形的判定和性质互为逆定理 .
知2-讲
感悟新知
特别提醒
矩形判定的常见思路:
从角上证明:
(1)四边形矩形;
(2)平行四边形矩形.
从对角线上证明:
(1)平行四边形矩形;
(2)四边形 矩形 .
知2-练
感悟新知
如图 2.5-6, 在四边形 ABCD 中, ∠ A= ∠ BCD=90°,BC=CD, CE ⊥ AD,垂足为 E,求证: AE=CE.
例4
知2-练
感悟新知
解题秘方:观察几何图形可知,无法用全等三角形等知识直接证明 AE=CE,因此可选择过点 B 作一条垂线段,同时构造一个矩形和一对全等三角形,借助中间量间接证得两条线段相等 .
知2-练
感悟新知
证明: 如图 2.5-6,过点 B 作 BF ⊥ CE 于点 F.
∵ CE ⊥ AD,∴∠ D+ ∠ DCE=90° .
∵∠ BCD=90°,∴∠ BCF+ ∠ DCE=90°,
∴∠ BCF= ∠ D.
在△ BCF 和△ CDE 中,
知2-练
感悟新知
∴△ BCF ≌△ CDE( AAS),∴ BF=CE.
∵ CE ⊥ AD, BF ⊥ CE,∴∠ AEF=90°,∠ BFE=90° .
又∵∠ A=90°,∴四边形 AEFB 是矩形,
∴ AE=BF,∴ AE=CE.
知2-练
感悟新知
方法点拨
本题通过作垂线段,利用“AAS”得到△BCF≌△CDE,再利用“有三个角是直角的四边形是矩形”得到四边形AEFB是矩形,最后根据全等三角形和矩形的性质得到线段相等 .
知2-练
感悟新知
[ 中考·长沙 ]如图 2.5-7, ABCD 的对角线 AC, BD相交于点 O,△ OAB 是等边三角形, AB=4.
(1)求证: ABCD 是矩形;
(2)求 AD 的长 .
例5
知2-练
感悟新知
解题秘方:紧扣“平行四边形”这一前提,从“对角线相等” 入手(或有一个角是直角入手)进行证明 .
知2-练
感悟新知
(1)证明: ∵四边形 ABCD 是平行四边形,
∴ 2OA=AC,2OB=BD.
∵△ OAB 是等边三角形,
∴ OA=OB,∴ AC=BD,∴ ABCD 是矩形 .
知2-练
感悟新知
(2)解: ∵△ OAB 是等边三角形, AB=4,
∴ OB=AB=4,∴ BD=2OB=8.
∵ ABCD 是矩形,∴∠ BAD=90°,
∴在 Rt △ ABD 中, AD= = =4 .
知2-练
感悟新知
方法点拨
证明一个平行四边形为矩形的两种方法:一种是证明有一个角是直角;另一种是证明两条对角线相等 .
矩形
矩形
性质
判定
定义
角的关系
对角线的关系
边的性质
角的性质
对角线的性质
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
