【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修二同步课件:2.2.1线面平行的判定(共19张PPT)
文档属性
| 名称 | 【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修二同步课件:2.2.1线面平行的判定(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-26 23:38:38 | ||
图片预览



文档简介
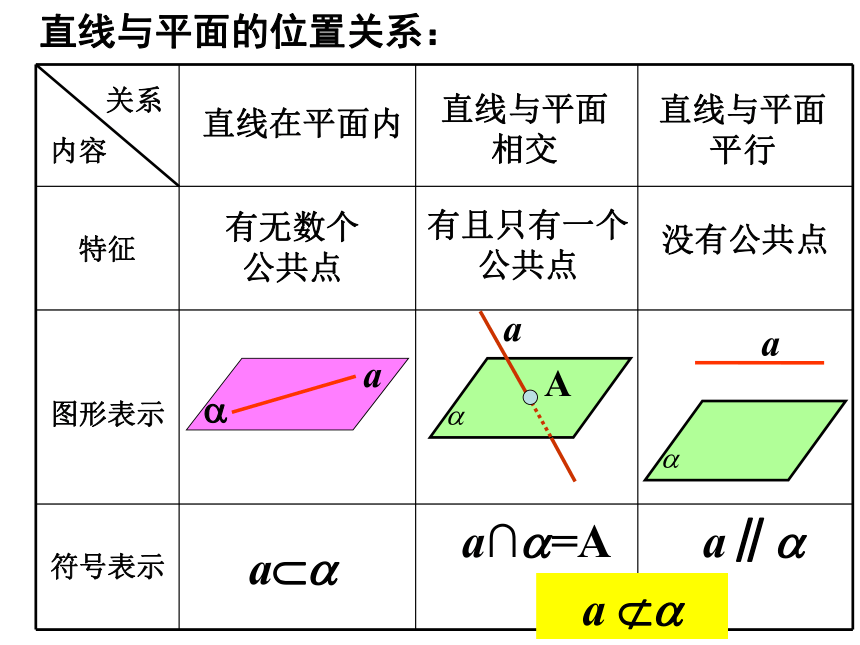
课件19张PPT。2.2.1直线与平面平行的判定内容关系直线在平面内直线与平面
相交直线与平面
平行有无数个
公共点有且只有一个
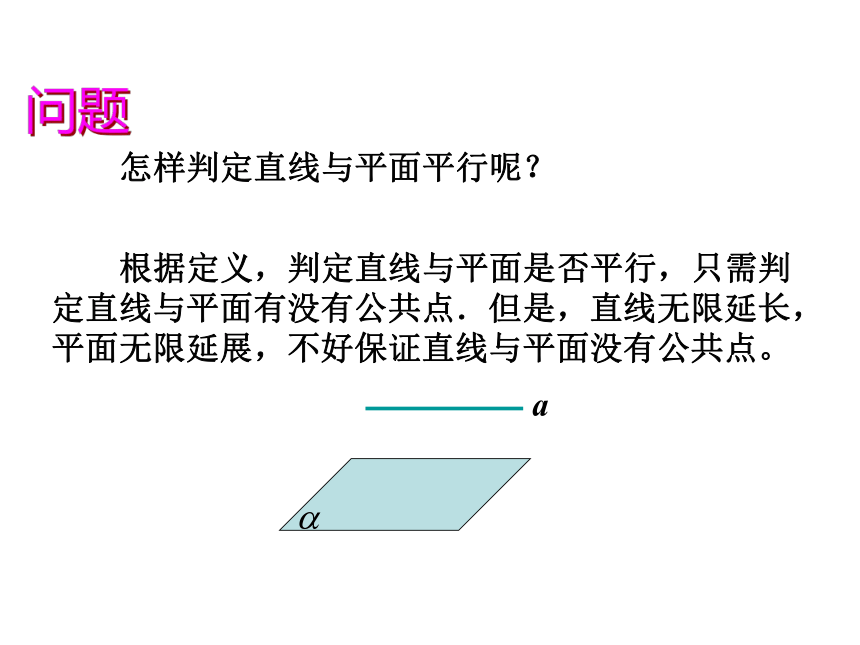
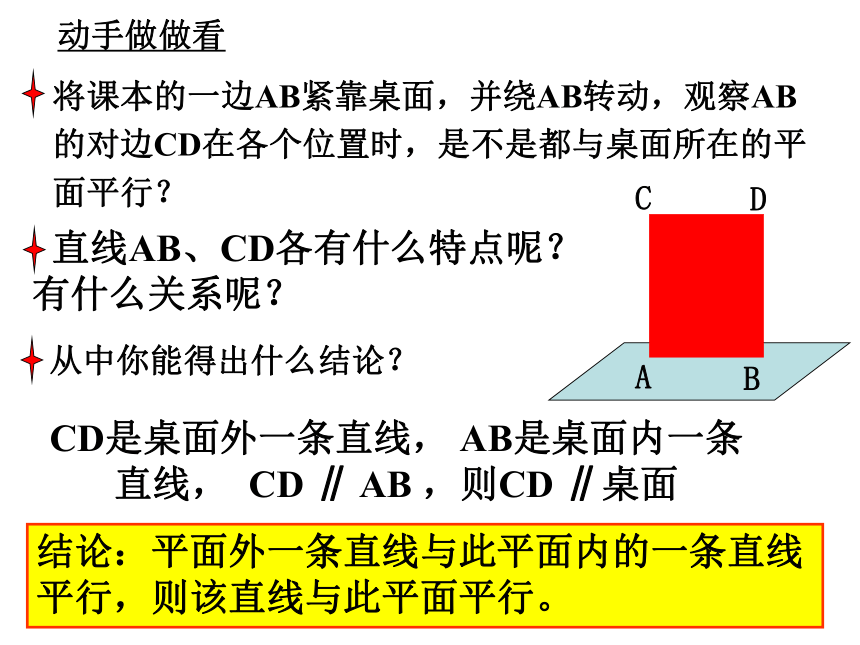
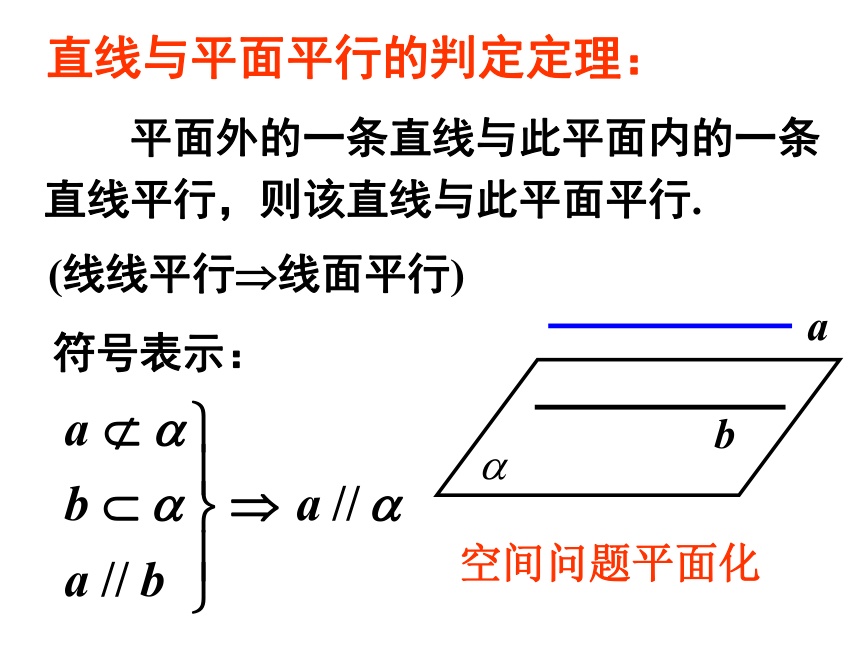
公共点没有公共点aa??a∩?=Aa∥?a ??直线与平面的位置关系: 怎样判定直线与平面平行呢?问题 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线无限延长,平面无限延展,不好保证直线与平面没有公共点。动手做做看将课本的一边AB紧靠桌面,并绕AB转动,观察AB 的对边CD在各个位置时,是不是都与桌面所在的平 面平行?ABCDCD是桌面外一条直线, AB是桌面内一条直线, CD ∥ AB ,则CD ∥桌面结论:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。符号表示: 平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理:空间问题平面化 (1)定义法:证明直线与平面无公共点; (2)判定定理: 怎样判定直线与平面平行?感受校园生活中线面平行的例子:球场地面感受校园生活中线面平行的例子:判断下列命题是否正确?(1)若平面 外一条直线a与直线b平行,
则直线a//平面 ;(2)若直线a与平面内一条直线b平行,
则直线a//平面 ;(3)直线a在平面外,直线b在平面内,
则直线a//平面 ;(4)直线a在平面外,直线b在平面内,
若a//b,则直线a//平面 ;(5)若a//平面 ,则a平行于 内的任何直线;(6)若a与平面 内的无数条直线平行,则a//平面 .判断下列命题是否正确?定理的应用 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
求证:EF∥平面BCD.ABCDEF 分析:要证明线面平行只需证明线线平行,即在平面BCD内找一条直线 平行于EF,由已知的条件怎样找这条直线?证明:连结BD.
∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质) 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
求证:EF∥平面BCD.ABDEF定理的应用1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCD变式1:ABCDEF∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,BDFO 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.证明:连结OF,ACE变式2:
1.线面平行,通常可以转化为线线平行来处理.反思~领悟:2.寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。
3、证明的书写三个条件“内”、“外”、“平行”,缺一不可。 1.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ;平面平面平面平面平面平面巩固练习:巩固练习: 2.如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.O 证明:连结BD交AC于O,连结EO.
∵O 为矩形ABCD对角线的交点,
∴DO=OB,
又∵DE=ED1,
∴BD1//EO.
O巩固练习: 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.归纳小结,理清知识体系1.判定直线与平面平行的方法:(1)定义法:直线与平面没有公共点则线面平行;(2)判定定理:(线线平行 线面平行);2.用定理证明线面平行时,在寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。
3.数学思想方法:转化的思想,空间问题转化为平面问题
相交直线与平面
平行有无数个
公共点有且只有一个
公共点没有公共点aa??a∩?=Aa∥?a ??直线与平面的位置关系: 怎样判定直线与平面平行呢?问题 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线无限延长,平面无限延展,不好保证直线与平面没有公共点。动手做做看将课本的一边AB紧靠桌面,并绕AB转动,观察AB 的对边CD在各个位置时,是不是都与桌面所在的平 面平行?ABCDCD是桌面外一条直线, AB是桌面内一条直线, CD ∥ AB ,则CD ∥桌面结论:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。符号表示: 平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理:空间问题平面化 (1)定义法:证明直线与平面无公共点; (2)判定定理: 怎样判定直线与平面平行?感受校园生活中线面平行的例子:球场地面感受校园生活中线面平行的例子:判断下列命题是否正确?(1)若平面 外一条直线a与直线b平行,
则直线a//平面 ;(2)若直线a与平面内一条直线b平行,
则直线a//平面 ;(3)直线a在平面外,直线b在平面内,
则直线a//平面 ;(4)直线a在平面外,直线b在平面内,
若a//b,则直线a//平面 ;(5)若a//平面 ,则a平行于 内的任何直线;(6)若a与平面 内的无数条直线平行,则a//平面 .判断下列命题是否正确?定理的应用 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
求证:EF∥平面BCD.ABCDEF 分析:要证明线面平行只需证明线线平行,即在平面BCD内找一条直线 平行于EF,由已知的条件怎样找这条直线?证明:连结BD.
∵AE=EB,AF=FD
∴EF∥BD(三角形中位线性质) 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
求证:EF∥平面BCD.ABDEF定理的应用1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCD变式1:ABCDEF∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,BDFO 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.证明:连结OF,ACE变式2:
1.线面平行,通常可以转化为线线平行来处理.反思~领悟:2.寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。
3、证明的书写三个条件“内”、“外”、“平行”,缺一不可。 1.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ;平面平面平面平面平面平面巩固练习:巩固练习: 2.如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.O 证明:连结BD交AC于O,连结EO.
∵O 为矩形ABCD对角线的交点,
∴DO=OB,
又∵DE=ED1,
∴BD1//EO.
O巩固练习: 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,求证:BD1//平面AEC.归纳小结,理清知识体系1.判定直线与平面平行的方法:(1)定义法:直线与平面没有公共点则线面平行;(2)判定定理:(线线平行 线面平行);2.用定理证明线面平行时,在寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。
3.数学思想方法:转化的思想,空间问题转化为平面问题
