【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修二同步课件:4.2.1直线和圆的位置关系(共15张PPT)
文档属性
| 名称 | 【全国百强校】内蒙古元宝山区平煤高级中学高中数学人教版必修二同步课件:4.2.1直线和圆的位置关系(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 75.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-26 19:37:42 | ||
图片预览




文档简介
课件15张PPT。4.2.1 直线与圆的位置关系点和圆的位置关系有几种?如何判定? 三种:点在圆外;点在圆上;点在圆内。复习提问:设点P(x0,y0),圆(x-a)2+(y-b)2=r2,
圆心(a,b)到P(x0,y0)的距离为d代数法:点在圆内?(x0 -a)2+(y0 -b)2<r2
点在圆上?(x0 -a)2+(y0 -b)2=r2
点在圆外?(x0 -a)2+(y0 -b)2>r2几何法:点在圆内?d 点在圆上?d=r
点在圆外?d>r点和圆的位置关系有几种?如何判定? 三种:点在圆外;点在圆上;点在圆内。代数法:点在圆内?(x0 -a)2+(y0 -b)2<r2
点在圆上?(x0 -a)2+(y0 -b)2=r2
点在圆外?(x0 -a)2+(y0 -b)2>r2几何法:点在圆内?d 点在圆上?d=r
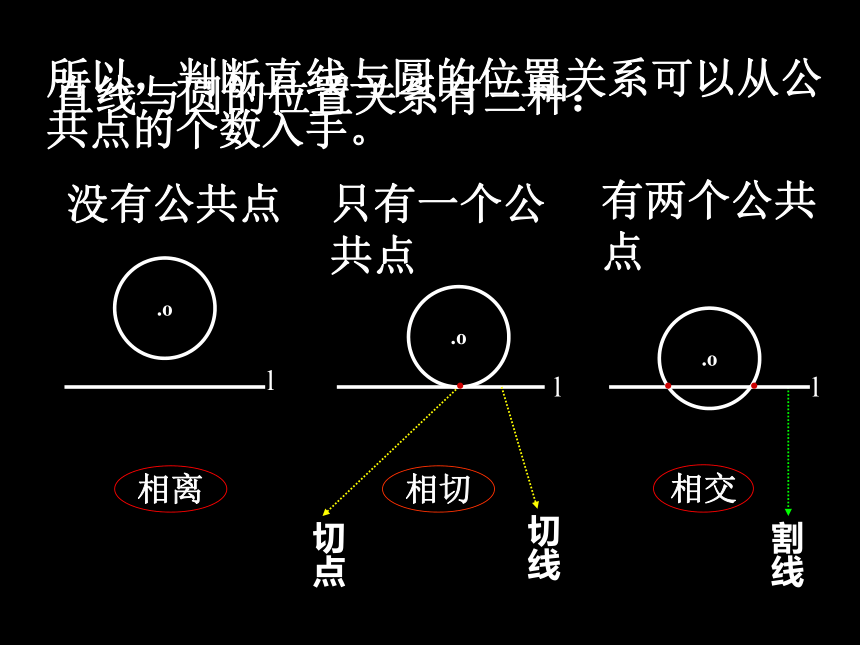
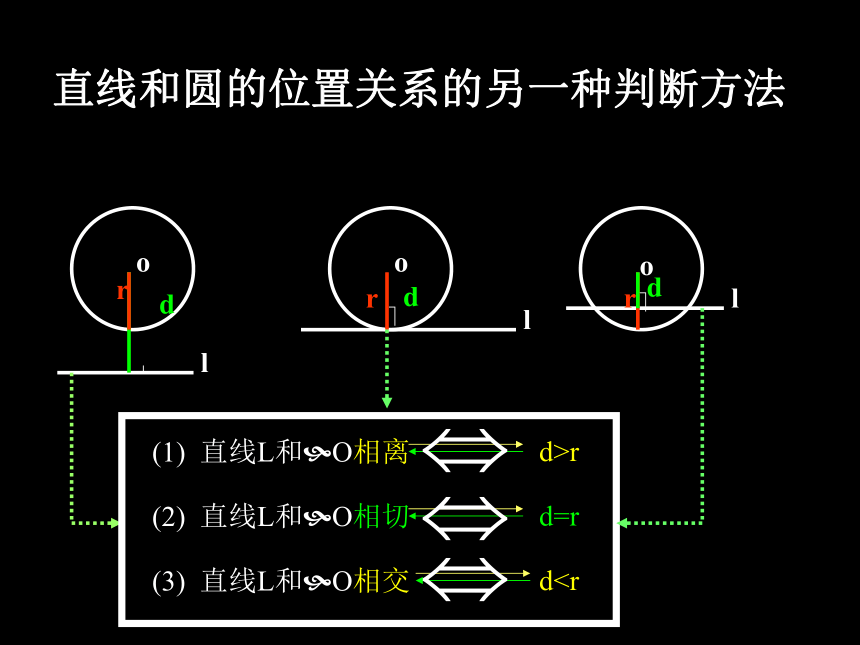
点在圆外?d>r那么直线与圆的位置关系有几种呢?直线与圆的位置关系有三种:相离相切相交切点切线割线l.o.o.oll...没有公共点只有一个公共点有两个公共点所以,判断直线与圆的位置关系可以从公共点的个数入手。 直线和圆的位置关系的另一种判断方法 ordo?rdo?lll (1) 直线L和?O相离d>r(2) 直线L和?O相切d=r(3) 直线L和?O相交d方法一:直线:Ax+By+C=0;圆:x2 + y2 +Dx+Ey+F=0
消元
一元二次方程
方法二:直线:Ax+By+C=0;圆: (x-a)2 + (y-b)2 =r2
d=
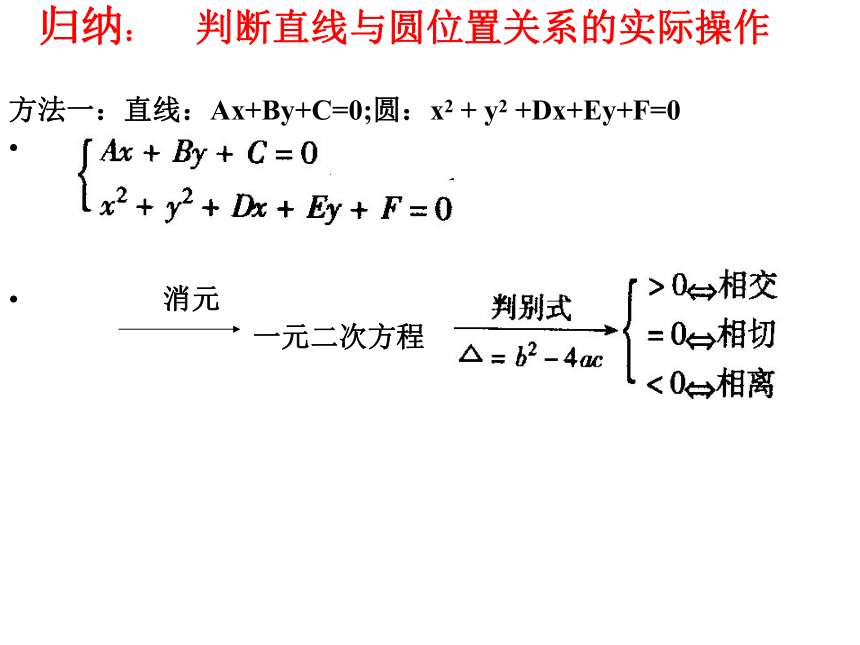
归纳: 判断直线与圆位置关系的实际操作
方法一:直线:Ax+By+C=0;圆:x2 + y2 +Dx+Ey+F=0
消元
一元二次方程
方法二:直线:Ax+By+C=0;圆: (x-a)2 + (y-b)2 =r2
d=
判断直线和圆的位置关系:几何角度求圆心坐标及
半径r 圆心到直线的距离d
(点到直线距离公式)代数角度 消去y(或x)
解法一:求解方程组,判定Δ解法二:利用直线与圆的位置关系判定d与r大小相离:K<-2√5 或k> 2√5;
相交:-2√5<K<2√5 ;
相切:k=± 2√5例1.K为何值时直线2x+y=k与圆x2+y2=4
相交;相切;相离。
例2:求过圆x2 + y2 +2x-4y+1=0外一点 p(-3,-2)的圆切线方程。解:设所求直线为y+2=k(x+3)代入圆方 程使Δ=0解得 K=3/4
即所求直线为3x-4y+1=0
提问:上述解题过程是否存在问题?说明:求直线方程时如果用到直线斜率,必须考虑直线斜率是否存在,否则容易丢解。
法一:求出交点利用两点间距离公式;法二:垂径定理例3:直线x-2y+5=0与圆x2 + y2 =25相交截得的 弦长。例4:已知圆C: (x-1)2 + (y-2)2 = 25及直线L(2m+1)x+(m+1)y=7m+4(m 为实数)
求证:不论m取什么实数直线L和圆C恒相交。解法一:利用圆心到直线距离解法二:借助于“判别式”解法三:直线L过定点,研究此点与圆的位置关系(一般)(不可取)(巧妙)1、 直线和圆的位置关系有三种( 相离、相切、相割)2、直线和圆位置关系的性质与判定( r与d的数量大小关系) (1) 直线L和?O相离d>r(2) 直线L和?O相切(3) 直线L和?O相交d=rd
曲线y=1+ √ 4- x2 (-2≤ x ≤ 2)与直线y=k(x-2)+4有两个交点时,实数K的取值范围是( )
A (5/12,3/4]B (5/12,+∞) C(1/3,3/4) D(0,5/12)
圆心(a,b)到P(x0,y0)的距离为d代数法:点在圆内?(x0 -a)2+(y0 -b)2<r2
点在圆上?(x0 -a)2+(y0 -b)2=r2
点在圆外?(x0 -a)2+(y0 -b)2>r2几何法:点在圆内?d
点在圆外?d>r点和圆的位置关系有几种?如何判定? 三种:点在圆外;点在圆上;点在圆内。代数法:点在圆内?(x0 -a)2+(y0 -b)2<r2
点在圆上?(x0 -a)2+(y0 -b)2=r2
点在圆外?(x0 -a)2+(y0 -b)2>r2几何法:点在圆内?d
点在圆外?d>r那么直线与圆的位置关系有几种呢?直线与圆的位置关系有三种:相离相切相交切点切线割线l.o.o.oll...没有公共点只有一个公共点有两个公共点所以,判断直线与圆的位置关系可以从公共点的个数入手。 直线和圆的位置关系的另一种判断方法 ordo?rdo?lll (1) 直线L和?O相离d>r(2) 直线L和?O相切d=r(3) 直线L和?O相交d
消元
一元二次方程
方法二:直线:Ax+By+C=0;圆: (x-a)2 + (y-b)2 =r2
d=
归纳: 判断直线与圆位置关系的实际操作
方法一:直线:Ax+By+C=0;圆:x2 + y2 +Dx+Ey+F=0
消元
一元二次方程
方法二:直线:Ax+By+C=0;圆: (x-a)2 + (y-b)2 =r2
d=
判断直线和圆的位置关系:几何角度求圆心坐标及
半径r 圆心到直线的距离d
(点到直线距离公式)代数角度 消去y(或x)
解法一:求解方程组,判定Δ解法二:利用直线与圆的位置关系判定d与r大小相离:K<-2√5 或k> 2√5;
相交:-2√5<K<2√5 ;
相切:k=± 2√5例1.K为何值时直线2x+y=k与圆x2+y2=4
相交;相切;相离。
例2:求过圆x2 + y2 +2x-4y+1=0外一点 p(-3,-2)的圆切线方程。解:设所求直线为y+2=k(x+3)代入圆方 程使Δ=0解得 K=3/4
即所求直线为3x-4y+1=0
提问:上述解题过程是否存在问题?说明:求直线方程时如果用到直线斜率,必须考虑直线斜率是否存在,否则容易丢解。
法一:求出交点利用两点间距离公式;法二:垂径定理例3:直线x-2y+5=0与圆x2 + y2 =25相交截得的 弦长。例4:已知圆C: (x-1)2 + (y-2)2 = 25及直线L(2m+1)x+(m+1)y=7m+4(m 为实数)
求证:不论m取什么实数直线L和圆C恒相交。解法一:利用圆心到直线距离解法二:借助于“判别式”解法三:直线L过定点,研究此点与圆的位置关系(一般)(不可取)(巧妙)1、 直线和圆的位置关系有三种( 相离、相切、相割)2、直线和圆位置关系的性质与判定( r与d的数量大小关系) (1) 直线L和?O相离d>r(2) 直线L和?O相切(3) 直线L和?O相交d=rd
曲线y=1+ √ 4- x2 (-2≤ x ≤ 2)与直线y=k(x-2)+4有两个交点时,实数K的取值范围是( )
A (5/12,3/4]B (5/12,+∞) C(1/3,3/4) D(0,5/12)
