人教版七年级上册6.3.3余角和补角 课件(共19张PPT)
文档属性
| 名称 | 人教版七年级上册6.3.3余角和补角 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 14:15:23 | ||
图片预览




文档简介
(共19张PPT)
第六章 几何图形初步
人教版七年级上册
6.3.3余角和补角
教学目标
1.了解余角补角的概念,能正确计算一个角的余角补角.
2.掌握余角补角的性质.
新知导入
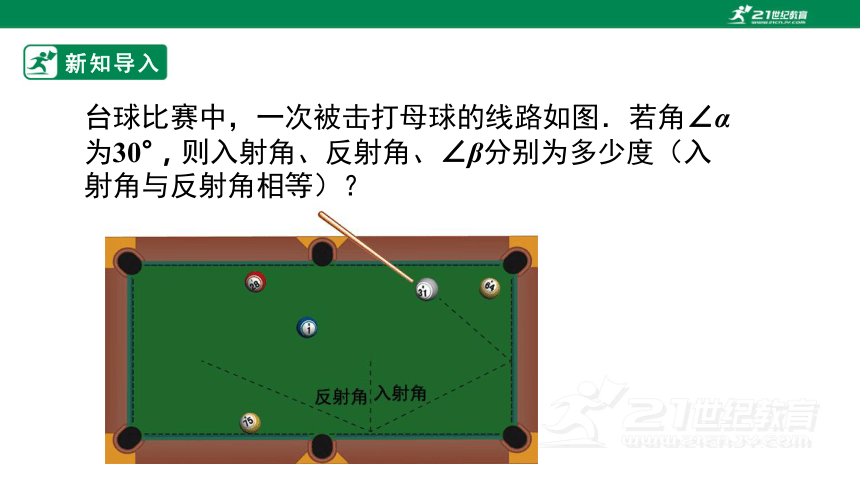
台球比赛中,一次被击打母球的线路如图.若角∠α为30°,则入射角、反射角、∠β分别为多少度(入射角与反射角相等)?
新知讲解
观察,∠1+∠2与 直角∠AOB 相等吗?你是怎样判断的?
1
2
A
O
B
观察 ,∠α+∠β与 ∠AOB 相等吗?你是怎样判断的?
α
β
新知讲解
在一副三角尺中,每块都有一个角是90o,而其他两个角的和是多少呢?
1
2
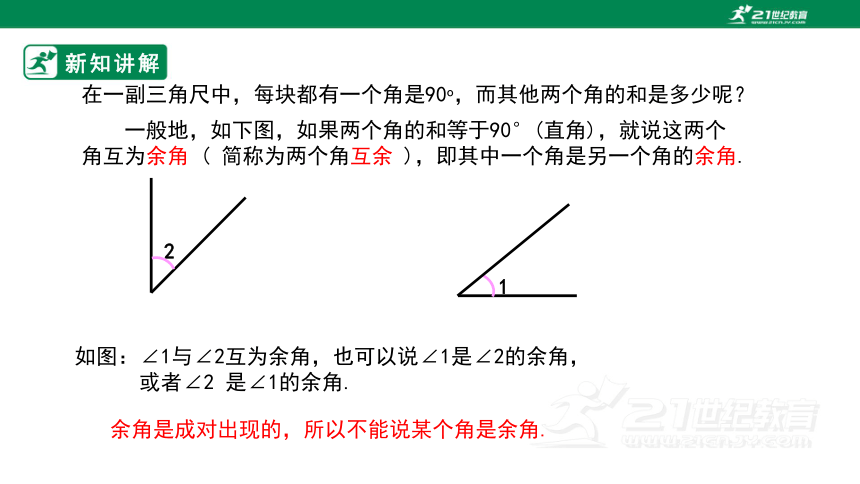
一般地,如下图,如果两个角的和等于90°(直角),就说这两个角互为余角 ( 简称为两个角互余 ),即其中一个角是另一个角的余角.
如图:∠1与∠2互为余角,也可以说∠1是∠2的余角,
或者∠2 是∠1的余角.
余角是成对出现的,所以不能说某个角是余角.
新知讲解
类似地,如下图,如果两个角的和等于180°(平角),就说这两个角互为补角( 简称为两个角互补 ),即其中一个角是另一个角的补角.
4
3
补角是成对出现的,所以不能说某个角是补角.
如图:∠3与∠4互为补角,也可以说∠3是∠4的补角,
或者∠4是∠3的补角.
新知讲解
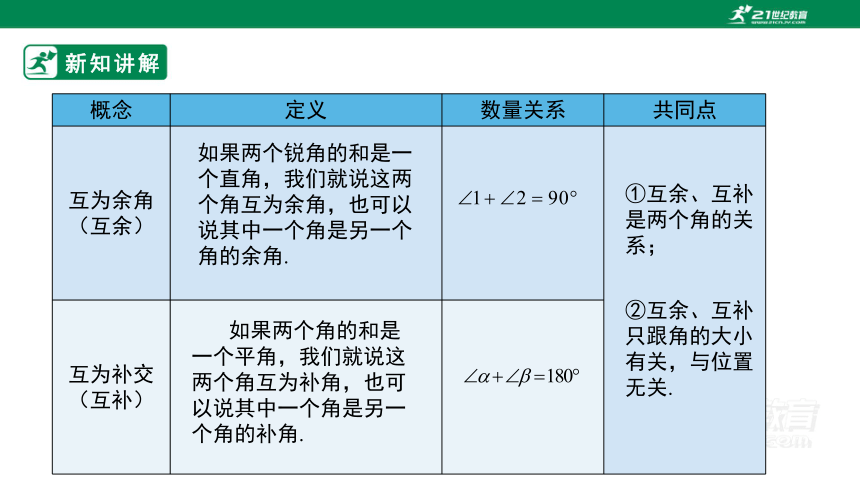
概念 定义 数量关系 共同点
互为余角 (互余)
互为补交 (互补) 如果两个锐角的和是一个直角,我们就说这两个角互为余角,也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,也可以说其中一个角是另一个角的补角.
①互余、互补是两个角的关系;
②互余、互补只跟角的大小有关,与位置无关.
新知讲解
3、 1与 2互补,除用符号语言表示为 1+ 2=180°外,还可以用其它形式等式表示为什么?
思考:
1、定义中的“互为”一词如何理解?
2、互补、互余的两角是否一定有公共顶点或公共边?
如果 1与 2互余,那么 1的余角是 2, 2的余角是 1.
互补或互余的两角不一定有公共顶点或公共边.
1=180°- 2,或 2=180°- 1.
新知讲解
思考:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
1
2
3
∠2=180°-∠1
∠3=180°-∠1
=
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
课堂练习
1.图中给出的各角中,哪些互为余角?哪些互为补角?
12°
30°
60°
78°
102°
120°
150°
168°
⑧
①
②
③
④
⑤
⑥
⑦
解:互余的角有:①与④,②与③
互补的角有:①与⑧,②与⑦,③与⑥,④与⑤.
课堂练习
2.如图,已知∠1=46°,∠2=134°,∠3=44°.图中有没在互余或互补的角?若有,请把它们写出来,并说明理由.
解:∠1与∠3互余,∵∠1+∠3=90°,∴∠1与∠3互余.
∠1与∠2互补,∵∠1+∠2=180°,∴∠1与∠2互补.
课堂练习
3.已知∠A=65°,则∠A的补角等于( )
A.125° B.105°
C.115° D.95°
4.已知α=36°42′,则α的余角为( )
A.57°18′ B.52°18′
C.53°18′ D.36°43′
C
C
课堂练习
5.对于互补的下列说法中:
①∠A+∠B+∠C=90°,则∠A,∠B,∠C互补;
②若∠1是∠2的补角,则∠2是∠1的补角;
③同一个锐角的补角一定比它的余角大90°;
④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
课堂总结
6.如图,∠AOB=160°,∠AOD与∠DOC互余,∠BOD=90°,
求∠COD的度数.
解:因为∠AOB=160°,∠BOD=90°,
所以∠AOD=70°.
因为∠AOD与∠DOC互余,
所以∠AOD+∠DOC=90°.
所以∠COD=90°-∠AOD=90°-70°=20°.
课堂总结
7.一个角的补角是它的3倍,这个角是多少度
解:设这个角为x°, 则这个角的补角是(180-x)°.
由题意得180-x=3x,
解得: x=45,
则这个角的度数为45°.
板书设计
如果两个锐角的和是一个直角,我们就说这两个角互为余角,也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,也可以说其中一个角是另一个角的补角.
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
作业布置
1.课后习题6.3.
2.完成练习册本课时的习题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第六章 几何图形初步
人教版七年级上册
6.3.3余角和补角
教学目标
1.了解余角补角的概念,能正确计算一个角的余角补角.
2.掌握余角补角的性质.
新知导入
台球比赛中,一次被击打母球的线路如图.若角∠α为30°,则入射角、反射角、∠β分别为多少度(入射角与反射角相等)?
新知讲解
观察,∠1+∠2与 直角∠AOB 相等吗?你是怎样判断的?
1
2
A
O
B
观察 ,∠α+∠β与 ∠AOB 相等吗?你是怎样判断的?
α
β
新知讲解
在一副三角尺中,每块都有一个角是90o,而其他两个角的和是多少呢?
1
2
一般地,如下图,如果两个角的和等于90°(直角),就说这两个角互为余角 ( 简称为两个角互余 ),即其中一个角是另一个角的余角.
如图:∠1与∠2互为余角,也可以说∠1是∠2的余角,
或者∠2 是∠1的余角.
余角是成对出现的,所以不能说某个角是余角.
新知讲解
类似地,如下图,如果两个角的和等于180°(平角),就说这两个角互为补角( 简称为两个角互补 ),即其中一个角是另一个角的补角.
4
3
补角是成对出现的,所以不能说某个角是补角.
如图:∠3与∠4互为补角,也可以说∠3是∠4的补角,
或者∠4是∠3的补角.
新知讲解
概念 定义 数量关系 共同点
互为余角 (互余)
互为补交 (互补) 如果两个锐角的和是一个直角,我们就说这两个角互为余角,也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,也可以说其中一个角是另一个角的补角.
①互余、互补是两个角的关系;
②互余、互补只跟角的大小有关,与位置无关.
新知讲解
3、 1与 2互补,除用符号语言表示为 1+ 2=180°外,还可以用其它形式等式表示为什么?
思考:
1、定义中的“互为”一词如何理解?
2、互补、互余的两角是否一定有公共顶点或公共边?
如果 1与 2互余,那么 1的余角是 2, 2的余角是 1.
互补或互余的两角不一定有公共顶点或公共边.
1=180°- 2,或 2=180°- 1.
新知讲解
思考:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
1
2
3
∠2=180°-∠1
∠3=180°-∠1
=
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
课堂练习
1.图中给出的各角中,哪些互为余角?哪些互为补角?
12°
30°
60°
78°
102°
120°
150°
168°
⑧
①
②
③
④
⑤
⑥
⑦
解:互余的角有:①与④,②与③
互补的角有:①与⑧,②与⑦,③与⑥,④与⑤.
课堂练习
2.如图,已知∠1=46°,∠2=134°,∠3=44°.图中有没在互余或互补的角?若有,请把它们写出来,并说明理由.
解:∠1与∠3互余,∵∠1+∠3=90°,∴∠1与∠3互余.
∠1与∠2互补,∵∠1+∠2=180°,∴∠1与∠2互补.
课堂练习
3.已知∠A=65°,则∠A的补角等于( )
A.125° B.105°
C.115° D.95°
4.已知α=36°42′,则α的余角为( )
A.57°18′ B.52°18′
C.53°18′ D.36°43′
C
C
课堂练习
5.对于互补的下列说法中:
①∠A+∠B+∠C=90°,则∠A,∠B,∠C互补;
②若∠1是∠2的补角,则∠2是∠1的补角;
③同一个锐角的补角一定比它的余角大90°;
④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
课堂总结
6.如图,∠AOB=160°,∠AOD与∠DOC互余,∠BOD=90°,
求∠COD的度数.
解:因为∠AOB=160°,∠BOD=90°,
所以∠AOD=70°.
因为∠AOD与∠DOC互余,
所以∠AOD+∠DOC=90°.
所以∠COD=90°-∠AOD=90°-70°=20°.
课堂总结
7.一个角的补角是它的3倍,这个角是多少度
解:设这个角为x°, 则这个角的补角是(180-x)°.
由题意得180-x=3x,
解得: x=45,
则这个角的度数为45°.
板书设计
如果两个锐角的和是一个直角,我们就说这两个角互为余角,也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,也可以说其中一个角是另一个角的补角.
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
作业布置
1.课后习题6.3.
2.完成练习册本课时的习题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
