对数函数及其性质
图片预览







文档简介
课件23张PPT。对数函数及其性质(一)对数函数的概念与图象合肥一六八中学
刘大锐问题 北京青年报曾报道:潮白河底挖出冰冻古树可能是山杨,专家经过检测可推断树的埋藏时间 . 你知道专家是根据什么推断数的埋藏时间的吗?问题 湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%.
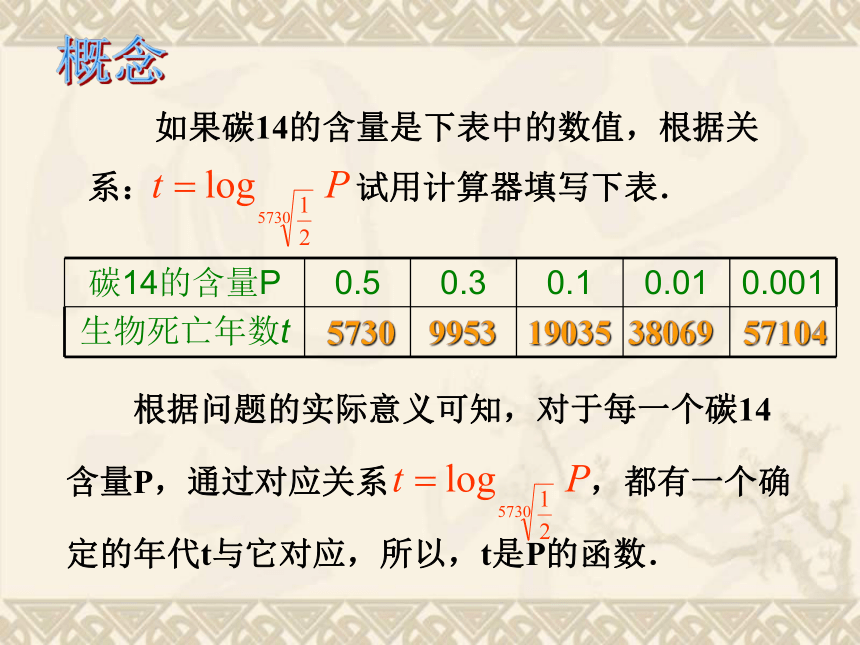
试推算马王堆古墓的年代. 人们经过长期实践,获得了生物体内碳14含量P与死亡年数t之间的关系:尝试解决 考古学家一般通过提取附着在出土文物.古遗址上死亡生物体的残留物,利用(*)式估算出土文物或古遗址的年代. 由指数与对数的关系,此指数式写成对数式是:(*) 现在,你能推算出马王堆古墓的年代吗?(P=76.7%)(t=2193)概念 如果碳14的含量是下表中的数值,根据关系: 试用计算器填写下表. 根据问题的实际意义可知,对于每一个碳14含量P,通过对应关系 ,都有一个确定的年代t与它对应,所以,t是P的函数.57309953190353806957104 一般地,函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,函数的定义域是( 0 , +∞).对数函数的定义:注意:1)对数函数定义的严格形式;,且2)对数函数对底数的限制条件:
在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
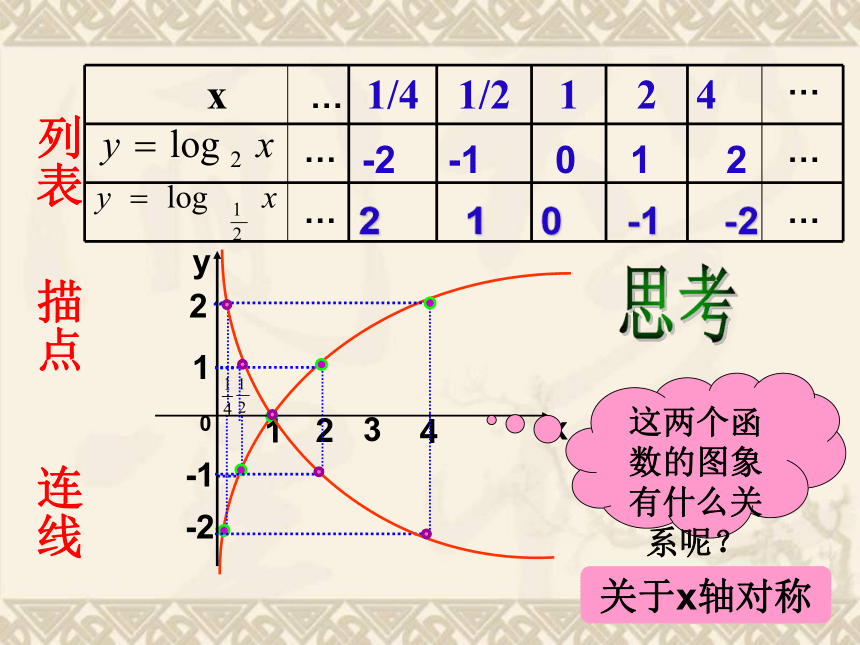
③用平滑曲线连接。探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质列表描点作y=log2x图象连线列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称… … … … … … 0 11(1)在同一坐标系中画出:
的图象. (2)你能否猜测 与 分别与哪个图象相似.xy对数函数:y = loga x (a>0,且a≠ 1) 图象与性质yxy=logaxy=logax图象性质a>10o 定义域 : (0,+??x=1时y=0 ;0x>1时,y>000
x>1时,y<0在(0,+??上是增函数 在(0,+??上是减函数值域:R对数函数的性质:图象特征 (1)完全分布在在y轴
右侧; (2)向上下无限延伸 并无限向y轴靠近,但永不相交 ; (3)过定点( 1 , 0 ); (4)在直线 x=1 两侧的两部分分别位于x轴的上方、下方; (5)从左至右观察图象, a>1时 呈上升趋势,0 < a<1时呈下降趋势。底数越大,图像越贴近x轴底数越大,图像越远离x轴例1求下列函数的定义域:(1) (2) 讲解范例 解 :解 :由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是例2 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 ∴ log23.4< log28.5解:考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5(2) log 0.3 1.8与 log 0.3 2.7解:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 方法归纳:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1;
( a>1时为增函数0即0 1(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0 ∴ loga5.1 > loga5.9你能口答吗?变一变还能口答吗?<,则m___n;则m___n.><>再变一下:比较下列各组中两个值的大小(1)(2)例 3 溶液酸碱度的测量.
溶液酸碱度是通过PH刻画的.PH值的计算公式为
PH=(1)根据对数函数的性质及上述PH的计算公式,说明溶液酸碱度
与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为
小结: (1)掌握对数函数的图像与性质,体会类比、
数形结合的思想方法;
(2)会利用对数函数的性质比较两个同底对数
值的大小,体会分类讨论的思想方法. 书面作业: 校本作业2.2.2课外作业:同步作业2.2.2第一课时
思考:比较a、b、c、d、1的大小。答:b>a>1>d>ccd a b y=1谢谢合作!
刘大锐问题 北京青年报曾报道:潮白河底挖出冰冻古树可能是山杨,专家经过检测可推断树的埋藏时间 . 你知道专家是根据什么推断数的埋藏时间的吗?问题 湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%.
试推算马王堆古墓的年代. 人们经过长期实践,获得了生物体内碳14含量P与死亡年数t之间的关系:尝试解决 考古学家一般通过提取附着在出土文物.古遗址上死亡生物体的残留物,利用(*)式估算出土文物或古遗址的年代. 由指数与对数的关系,此指数式写成对数式是:(*) 现在,你能推算出马王堆古墓的年代吗?(P=76.7%)(t=2193)概念 如果碳14的含量是下表中的数值,根据关系: 试用计算器填写下表. 根据问题的实际意义可知,对于每一个碳14含量P,通过对应关系 ,都有一个确定的年代t与它对应,所以,t是P的函数.57309953190353806957104 一般地,函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,函数的定义域是( 0 , +∞).对数函数的定义:注意:1)对数函数定义的严格形式;,且2)对数函数对底数的限制条件:
在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③用平滑曲线连接。探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质列表描点作y=log2x图象连线列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称… … … … … … 0 11(1)在同一坐标系中画出:
的图象. (2)你能否猜测 与 分别与哪个图象相似.xy对数函数:y = loga x (a>0,且a≠ 1) 图象与性质yxy=logaxy=logax图象性质a>10
x>1时,y<0在(0,+??上是增函数 在(0,+??上是减函数值域:R对数函数的性质:图象特征 (1)完全分布在在y轴
右侧; (2)向上下无限延伸 并无限向y轴靠近,但永不相交 ; (3)过定点( 1 , 0 ); (4)在直线 x=1 两侧的两部分分别位于x轴的上方、下方; (5)从左至右观察图象, a>1时 呈上升趋势,0 < a<1时呈下降趋势。底数越大,图像越贴近x轴底数越大,图像越远离x轴例1求下列函数的定义域:(1) (2) 讲解范例 解 :解 :由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是例2 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 ∴ log23.4< log28.5解:考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5(2) log 0.3 1.8与 log 0.3 2.7解:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 方法归纳:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1;
( a>1时为增函数0
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0
溶液酸碱度是通过PH刻画的.PH值的计算公式为
PH=(1)根据对数函数的性质及上述PH的计算公式,说明溶液酸碱度
与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为
小结: (1)掌握对数函数的图像与性质,体会类比、
数形结合的思想方法;
(2)会利用对数函数的性质比较两个同底对数
值的大小,体会分类讨论的思想方法. 书面作业: 校本作业2.2.2课外作业:同步作业2.2.2第一课时
思考:比较a、b、c、d、1的大小。答:b>a>1>d>ccd a b y=1谢谢合作!
