2.2.3向量数乘运算及其几何意义
文档属性
| 名称 | 2.2.3向量数乘运算及其几何意义 |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-27 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
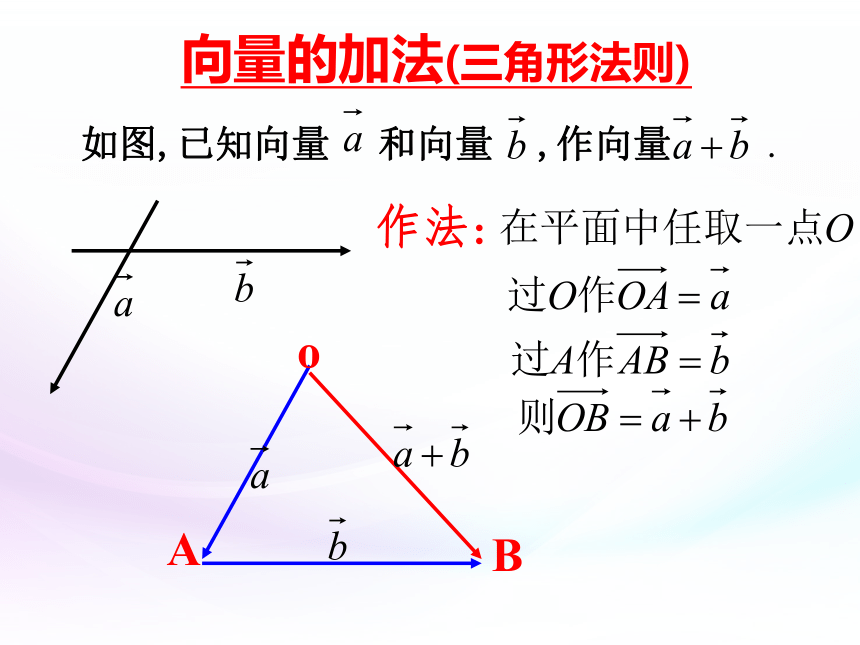
向量的加法(三角形法则)
如图,已知向量 和向量 ,作向量 .
作法:
A
B
o
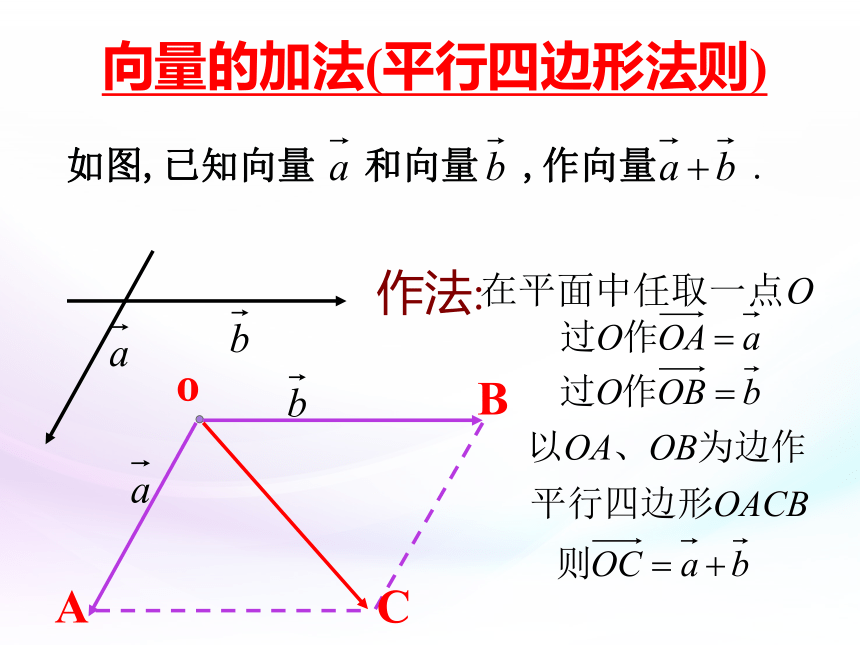
向量的加法(平行四边形法则)
作法:
o
A
B
C
如图,已知向量 和向量 ,作向量 .
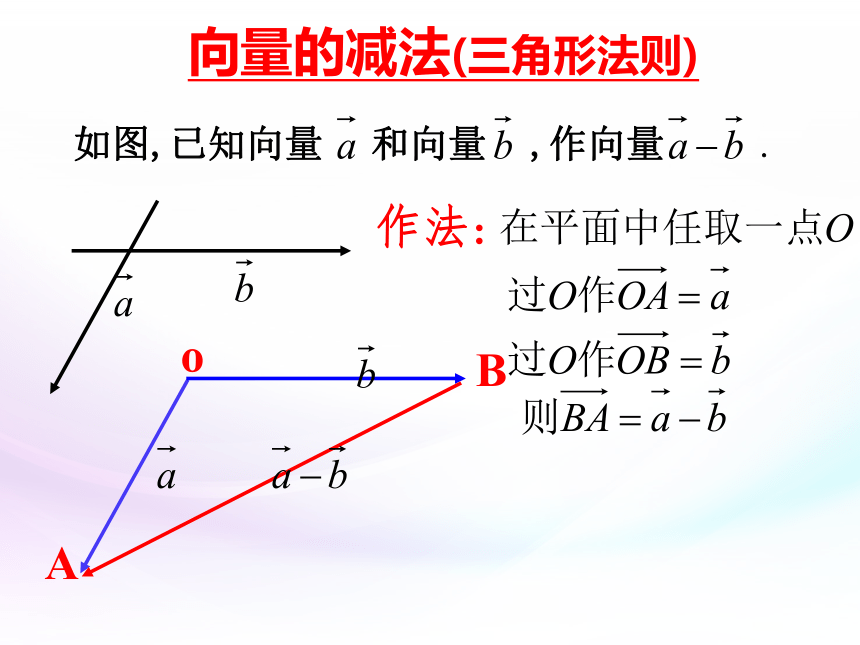
向量的减法(三角形法则)
如图,已知向量 和向量 ,作向量 .
作法:
A
B
o
2.2.3 向量数乘运算及其几何意义
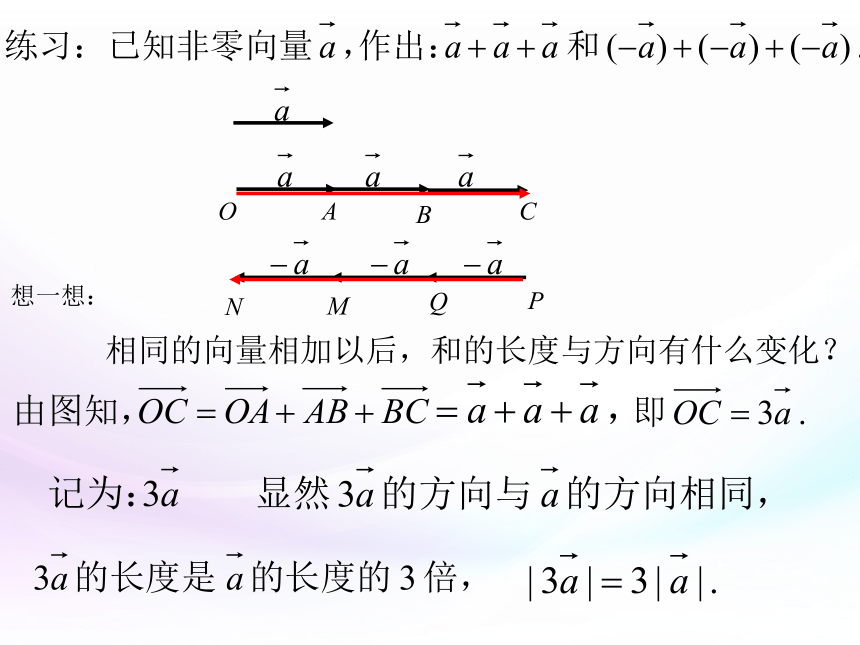
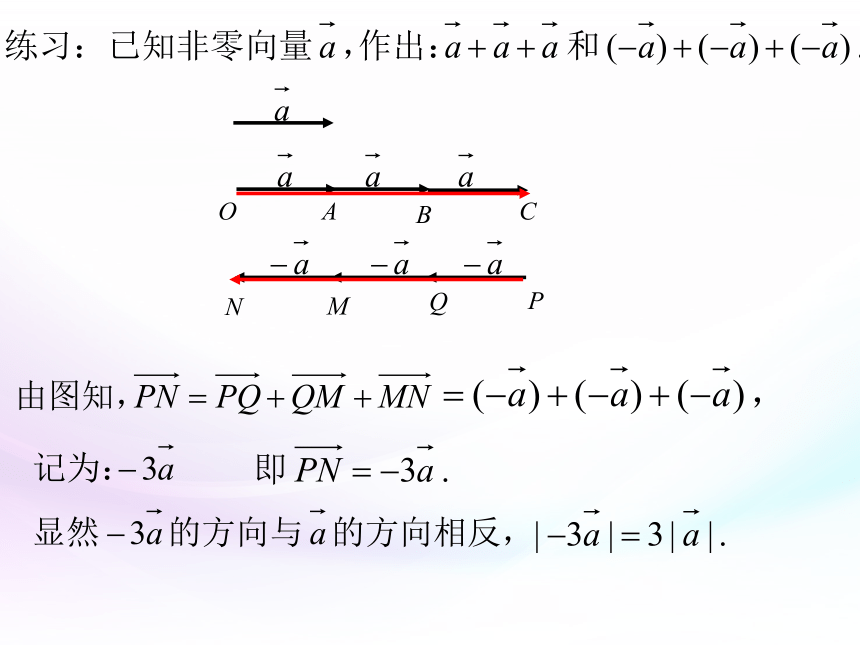
问题:通过上述的具体实例总结出更具一般性的向量数乘的定义
问题:你能说明它的几何意义吗?
注意:
在物理中位移与速度的关系:
其中位移、速度,力、加速度都是向量,
而时间、质量都是数量.
s = vt,
f = ma.
力与加速度的关系:
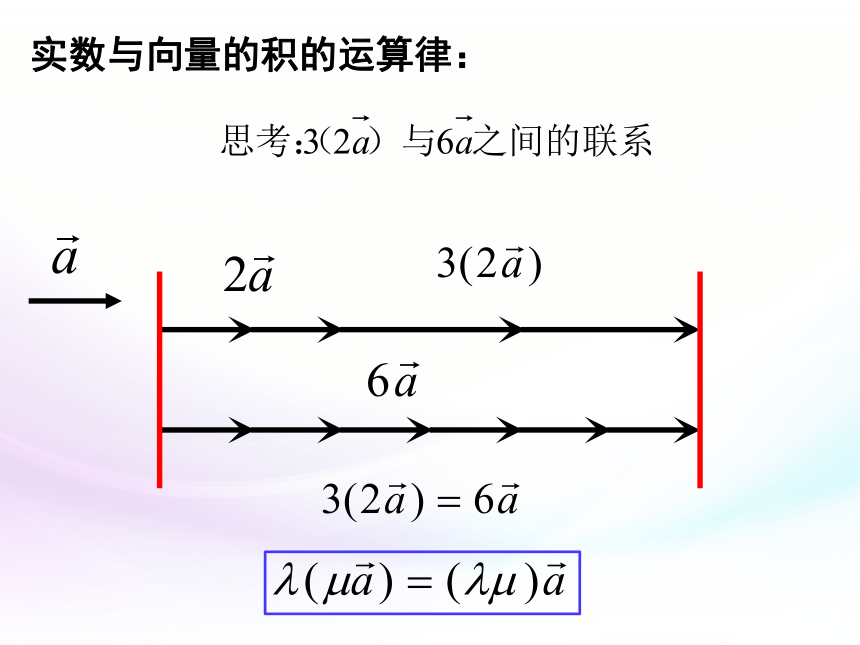
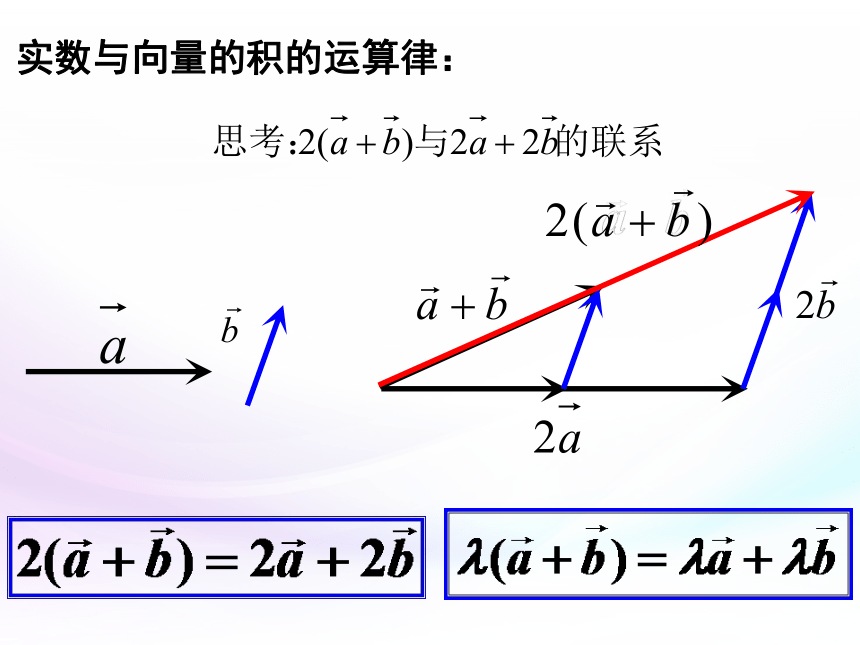
实数与向量的积的运算律:
实数与向量的积的运算律:
实数与向量的积的运算律:
向量的加、减、数乘运算统称为向量的线性运算。
课本P90 5
课本P90 5
教材P90 3
思考
结 论:
思考
结 论:
2) 可以是零向量吗
思考:1) 为什么要是非零向量
共线向量基本定理:
向量 与非零向量 共线当且仅当
有唯一一个实数 ,使得
课本P90 4
课本P90 2
3.已知|a|=5,|b|=4且a与b的方向相反,则a=________b.
全优90页限时规范训练
A
B
C
D
E
A
B
C
D
E
(2)证明三点共线的问题:
定理的应用:
(1)有关向量共线问题:
(3)证明两直线平行的问题:
例6:
解:作图如右
O
A
B
C
依图猜想:A、B、C三点共线
a
b
b
b
已知任意两非零向量a、b,
试作 OA=a+b, OB=a+2b, OC=a+3b。
你能判断A、B、C三点之间的位置关系吗?为什么?
b
a
又 AB与AC有公共点A,
∴ A、B、C三点共线.
7.已知e1,e2不共线,a=ke1+e2,b=e1+ke2,问k取何值时,a与b共线?
k=±1
全优48页能力提高
则实数λ的值是( )
D
全优90页限时规范训练
2.已知e1,e2是两个不共线向量,若向量m=-e1+ke2(k∈R)与向量n=e2-2e1共线,求k的值.
【解析】
因为m,n共线,
所以存在实数λ,
使m=λn,
即-e1+ke2=λ(e2-2e1),
全优47页变式训练
【例2】 设e1,e2是两个不共线向量,已知
若A,B,D三点共线,求k的值.
【解析】
而A,B,D三点共线,
故存在实数λ,
即2e1+ke2=λ(e1-4e2),
得k=-8为所求.
全优47页典例剖析
A
D
B
M
C
如图: ABCD的两条对角线交于点M,且 , 用 ,表示
例7:
8.如图,在 ABCD中,点M是AB的中点,点N在BD上且
求证:M,N,C三点共线.
【证明】
又MC,MN有公共点M.
所以M,N,C三点共线.
全优48页能力提高
向量的加法(三角形法则)
如图,已知向量 和向量 ,作向量 .
作法:
A
B
o
向量的加法(平行四边形法则)
作法:
o
A
B
C
如图,已知向量 和向量 ,作向量 .
向量的减法(三角形法则)
如图,已知向量 和向量 ,作向量 .
作法:
A
B
o
2.2.3 向量数乘运算及其几何意义
问题:通过上述的具体实例总结出更具一般性的向量数乘的定义
问题:你能说明它的几何意义吗?
注意:
在物理中位移与速度的关系:
其中位移、速度,力、加速度都是向量,
而时间、质量都是数量.
s = vt,
f = ma.
力与加速度的关系:
实数与向量的积的运算律:
实数与向量的积的运算律:
实数与向量的积的运算律:
向量的加、减、数乘运算统称为向量的线性运算。
课本P90 5
课本P90 5
教材P90 3
思考
结 论:
思考
结 论:
2) 可以是零向量吗
思考:1) 为什么要是非零向量
共线向量基本定理:
向量 与非零向量 共线当且仅当
有唯一一个实数 ,使得
课本P90 4
课本P90 2
3.已知|a|=5,|b|=4且a与b的方向相反,则a=________b.
全优90页限时规范训练
A
B
C
D
E
A
B
C
D
E
(2)证明三点共线的问题:
定理的应用:
(1)有关向量共线问题:
(3)证明两直线平行的问题:
例6:
解:作图如右
O
A
B
C
依图猜想:A、B、C三点共线
a
b
b
b
已知任意两非零向量a、b,
试作 OA=a+b, OB=a+2b, OC=a+3b。
你能判断A、B、C三点之间的位置关系吗?为什么?
b
a
又 AB与AC有公共点A,
∴ A、B、C三点共线.
7.已知e1,e2不共线,a=ke1+e2,b=e1+ke2,问k取何值时,a与b共线?
k=±1
全优48页能力提高
则实数λ的值是( )
D
全优90页限时规范训练
2.已知e1,e2是两个不共线向量,若向量m=-e1+ke2(k∈R)与向量n=e2-2e1共线,求k的值.
【解析】
因为m,n共线,
所以存在实数λ,
使m=λn,
即-e1+ke2=λ(e2-2e1),
全优47页变式训练
【例2】 设e1,e2是两个不共线向量,已知
若A,B,D三点共线,求k的值.
【解析】
而A,B,D三点共线,
故存在实数λ,
即2e1+ke2=λ(e1-4e2),
得k=-8为所求.
全优47页典例剖析
A
D
B
M
C
如图: ABCD的两条对角线交于点M,且 , 用 ,表示
例7:
8.如图,在 ABCD中,点M是AB的中点,点N在BD上且
求证:M,N,C三点共线.
【证明】
又MC,MN有公共点M.
所以M,N,C三点共线.
全优48页能力提高
