第三章《数据的分析》综合测试题(含答案)
文档属性
| 名称 | 第三章《数据的分析》综合测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章综合测试题
时间: 45分钟 满分: 100分
一、选择题(本大题共10小题,每小题3分,共30分)
1.根据某市统计局发布的该市近5年的年度GDP 增长率的有关数据,经济学家评论说,该市近5年的年度GDP 增长率相当平稳,从统计学的角度看,判断“增长率相当平稳”的依据是数据的( )
A.中位数 B.平均数 C.众数 D.方差
2.已知一组数据:-3,6,2,-1,0,4,则这组数据的中位数是 ( )
A. 1 B. C. 0 D. 2
3.若一组数据1,3,4,6,m的平均数为4,则这组数据的中位数和众数分别是 ( )
A. 4,4 B. 4,6 C. 3,6 D. 3,4
4.方差是刻画一组数据波动大小的量,对于一组数据可用如下算式计算方差: 其中“3”是这组数据的 ( )
A.最小值 B.平均数 C.众数 D.中位数
5.2022北京冬奥会期间,为了表达对志愿者工作的支持,某班学生积极参加捐款活动,该班50名学生的捐款统计情况如表:
金额/元 5 10 20 50 100
人数 6 17 14 8 5
则他们捐款金额的众数与中位数是 ( )
A. 20,10 B. 17,14 C. 10,20 D. 17,20
6.某校举办读书分享大赛活动,最终有13名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖3名.某参赛同学知道自己的分数后,要判断自己能否获奖,他需要知道这13名学生成绩的 ( )
A.中位数 B.平均数 C.众数 D.方差
7.小颖姐姐今年大学毕业了,她去一家公司参加招聘文员测试,公司对应试者进行了笔试和面试测试,再按笔试占60%、面试占40%计算应试者的总成绩,已知小颖姐姐笔试得85分、面试得75分,则她的总成绩为 ( )
A. 79分 B. 80分 C. 81分 D. 82分
8.甲、乙两位同学连续五次的数学成绩如图所示,下列说法正确的是 ( )
D.无法比较与的大小
9.一组数据:3,4,4,5.如果再添加一个数据4,那么会发生变化的统计量是 ( )
A.平均数 B.中位数 C.众数 D.方差
10.已知数据;数据B:.若数据A 的方差比数据B的方差小,则x的值可能是 ( )
A. 5 B. 4 C. 2 D. 0
二、填空题(本大题共6小题,每小题3分,共18分)
11.若一组数据的极差为9,则x的值是_________.
12.甲、乙两队参加“传承红色基因,推动绿色发展”为主题的合唱比赛,每队均由20名队员组成.其中两队队员的平均身高为 身高的方差分别为 如果单从队员的身高考虑,你认为演出形象效果较好的是_________队.
13.根据第七次全国人口普查,华东A,B,C,D,E,F六省60岁及以上人口占比情况如图所示,这六省60岁及以上人口占比的中位数是_________.
14.某小组6名学生的平均身高a cm,规定超a cm 的部分记为正数,不a cm的部分记为负数,他们的身高与平均身高的差值情况记录如表:
学生序号 1 2 3 4 5 6
身高差值(cm) +2 x +3 -1 -4 -1
据此判断,2号学生的身高为________ cm.(用含a的代数式表示)
15.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为_________.
16.在5个正整数a,b,c,d,e中,中位数是4,唯一的众数是6,则这5个数的和的最大值是__________.
三、解答题(本大题共7 小题,共52分)
17.(6分)某校决定从八年级两个班中选择一个班作为市级先进班级的候选班,现对这两个班进行综合素质考评,如表是这两个班五项考评的得分表(单位:分,每项满分为10分).
班级 道德行为/分 学习成绩/分 艺术获奖/分 劳动卫生/分 校运动会/分
八年级(1)班 9 8 7 9 7
八年级(2)班 8 9 8 9 8
如果将道德行为、学习成绩、艺术获奖、劳动卫生、校运动会五项得分按2:3:1:3:1的比例确定各班的最终得分,那么该校会选择哪个班作为市级先进班级的候选班
18.(6分)某公司随机抽取一名职工,统计了他一个月(30天)每天上班通勤费用,
通勤费用(元/天) 0元 4元 8元 36元
天数(天) 8 12 6 4
(1)该名职工上班通勤费用的中位数是_________,众数是_________;
(2)若该公司每天补贴该职工上班通勤费用6元,请你利用统计知识判断该职工是否还需自行补充上班通勤费用
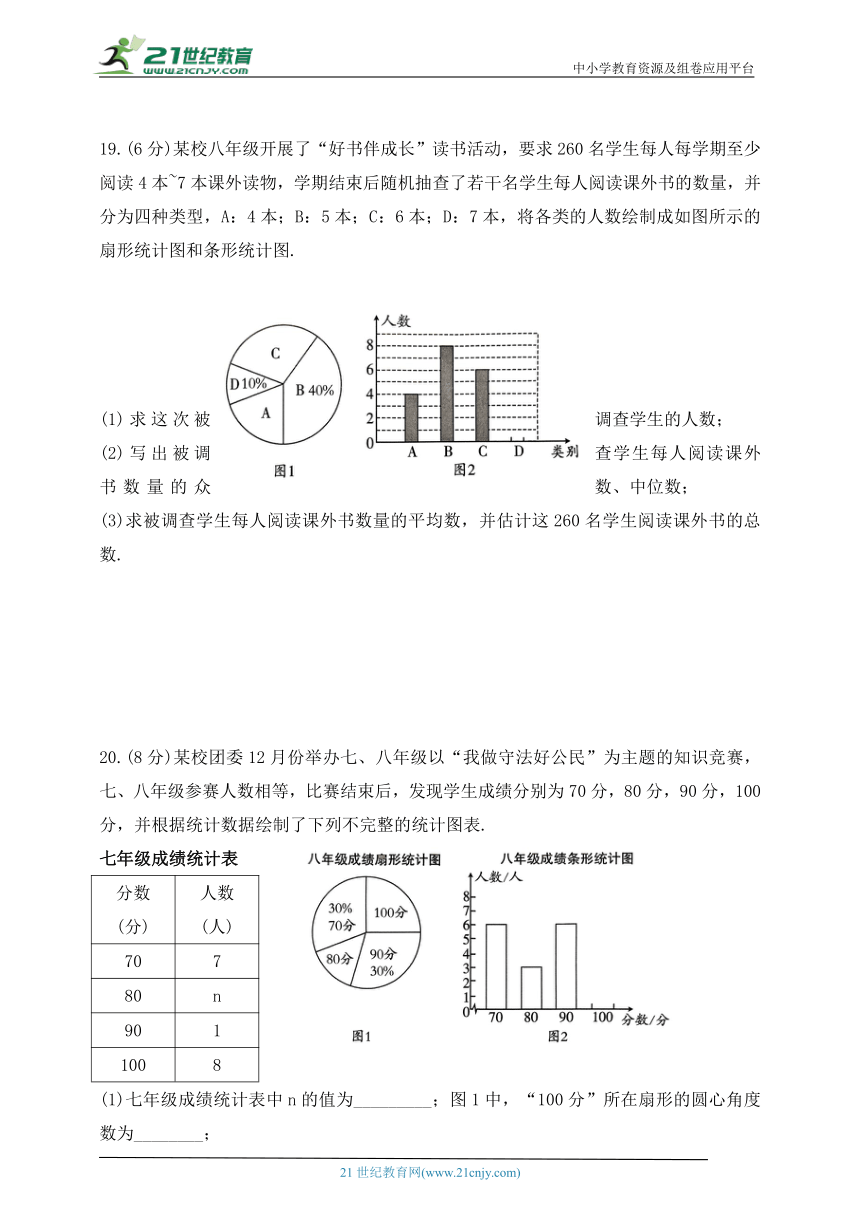
19.(6分)某校八年级开展了“好书伴成长”读书活动,要求260名学生每人每学期至少阅读4本~7本课外读物,学期结束后随机抽查了若干名学生每人阅读课外书的数量,并分为四种类型,A:4本;B:5本;C:6本;D:7本,将各类的人数绘制成如图所示的扇形统计图和条形统计图.
(1)求这次被调查学生的人数;
(2)写出被调查学生每人阅读课外书数量的众数、中位数;
(3)求被调查学生每人阅读课外书数量的平均数,并估计这260名学生阅读课外书的总数.
20.(8分)某校团委12月份举办七、八年级以“我做守法好公民”为主题的知识竞赛,七、八年级参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了下列不完整的统计图表.
七年级成绩统计表
分数(分) 人数(人)
70 7
80 n
90 1
100 8
(1)七年级成绩统计表中n的值为_________;图1中,“100分”所在扇形的圆心角度数为________;
(2)八年级成绩的中位数为_________分;七年级成绩的平均分为________分;
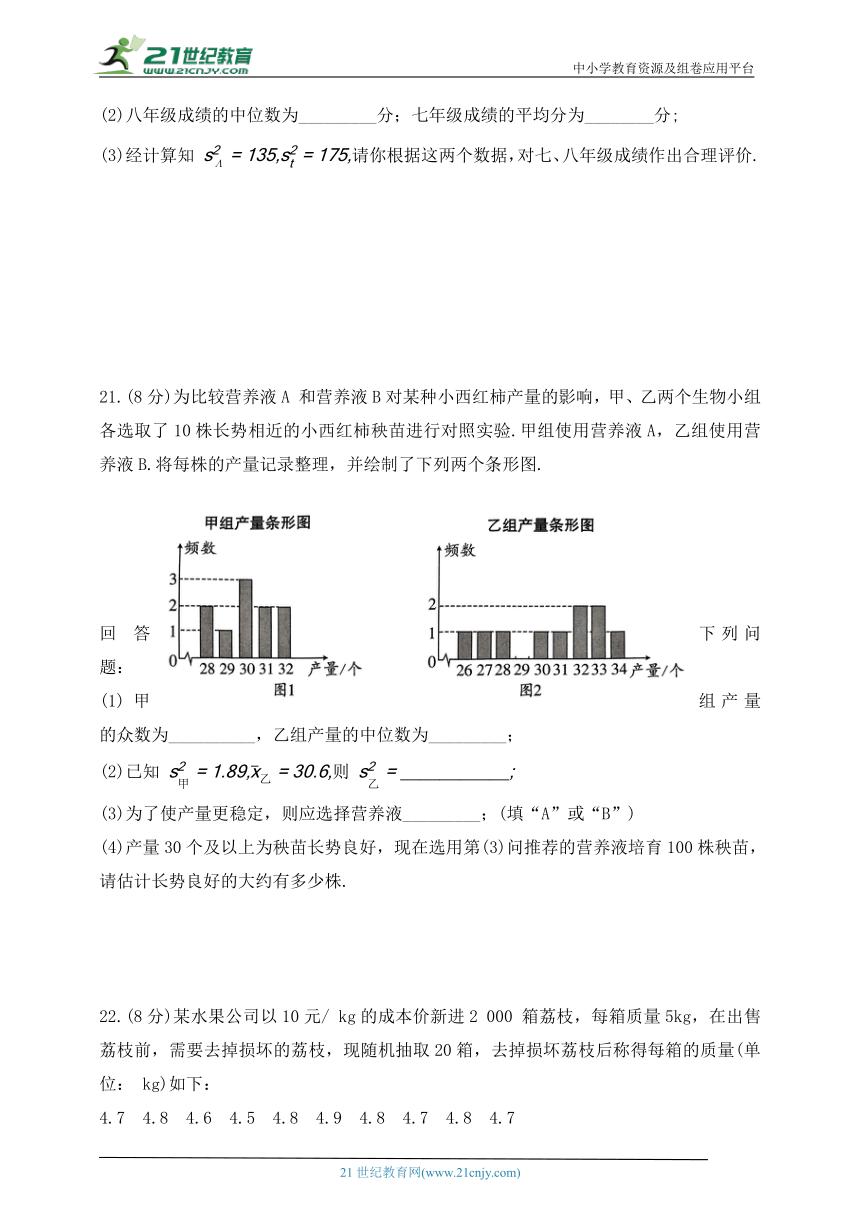
(3)经计算知 请你根据这两个数据,对七、八年级成绩作出合理评价.
21.(8分)为比较营养液A 和营养液B对某种小西红柿产量的影响,甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验.甲组使用营养液A,乙组使用营养液B.将每株的产量记录整理,并绘制了下列两个条形图.
回答下列问题:
(1)甲组产量的众数为__________,乙组产量的中位数为_________;
(2)已知 则
(3)为了使产量更稳定,则应选择营养液_________;(填“A”或“B”)
(4)产量30个及以上为秧苗长势良好,现在选用第(3)问推荐的营养液培育100株秧苗,请估计长势良好的大约有多少株.
22.(8分)某水果公司以10元/ kg的成本价新进2 000 箱荔枝,每箱质量5kg,在出售荔枝前,需要去掉损坏的荔枝,现随机抽取20箱,去掉损坏荔枝后称得每箱的质量(单位: kg)如下:
4.7 4.8 4.6 4.5 4.8 4.9 4.8 4.7 4.8 4.7
4.8 4.9 4.7 4.8 4.5 4.7 4.7 4.9 4.7 5.0
整理数据:
质量(kg) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b C
(1)直接写出上述表格中a,b,c的值;
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这2 000 箱荔枝共损坏了多少千克
(3)根据(2)中的结果,求该公司销售这批荔枝每千克定为多少元才不亏本(结果保留一位小数)
23.(10分)某篮球队,全员进行定点投篮训练,每人投五次,训练结束后,发现命中的结果只有2次、3次、4次、5次,并把结果制成了如图1,图2所示不完整的条形统计图和扇形统计图.
(1)“命中4次”所在扇形的圆心角是________;请将条形统计图补充完整;
(2)若有一名队员新加入篮球队,经过五次定点投篮后,把命中结果与原命中结果组成一组新数据,发现平均数变小,求此队员命中结果的最大值;
(3)若有n名队员新加入篮球队,经过五次定点投篮后,把命中结果与原命中结果组成一组新数据,发现中位数发生了变化,求n的最小值.
参考答案
1. D 2. A 3. B 4. B 5. C 6. A 7. C 8. B 9. D 10. C
11. -4 或8 12. 乙 13. 18.75% 14. (a+1) 15. 1 16. 21
17.解:八年级(1)班的最终得分为 (分),
八年级(2)班的最终得分为 (分),
∴该校会选择八年级(2)班作为市级先进班级的候选班.
18.解:(1)将这30天的该名职工上班通勤费用从小到大排列,第15 和第 16 两个数都是4元,因此中位数是4元,这30天的该名职工上班通勤费用出现次数最多的是4元,共出现12次,因此众数是4元,
故答案为:4元,4元;
(2)需要,理由如下:
这30天的该名职工上班通勤费用的平均数为 (元),
∵6<8,∴该职工还需要自行补充上班通勤费用.
19.解: (名).
答:这次被调查学生有20名;
(2)∵读了5本课外书的有8人,最多,
∴被调查学生阅读课外书数量的众数为5本;
∵共有 20人,∴中位数是第10人和第11人的平均数,
∴被调查学生阅读课外书数量的中位数为 (本);
(3)平均数为 (本);
估计这260名学生阅读课外书的总数约为 (本).
20.解:(1)参赛的人数为( (人),
七年级成绩统计表中
图1中,“100分”所在扇形的圆心角度数为
故答案为: 4,90°;
(2)∵一共有20人参赛,第10个数为90,第11个数为90,
∴八年级成绩的中位数为
七年级成绩的平均分为
故答案为:90,85;
∴八年级20名同学的成绩比较整齐.
21.解:(1)由条形统计图,得甲组产量的众数为30个,
乙组产量第5个数是31,第6个数是32,
乙组产量的中位数为 (个).
故答案为:30个,31.5个;
故答案为: 6.84;
(3)由(2),得
∴甲组方差较小,产量的波动较小,产量更稳定,
所以应选择营养液 A;
故答案为:A;
(4)估计长势良好的大约有 70(株).
答:估计长势良好的大约有70株.
22.解:(
分析数据:样本中,4.7出现的次数最多,故众数b为4.7;
将数据从小到大排列,找最中间的两个数为4.7,4.8,故中位数
综上所述,
(2)选择众数4.7,
这2000箱荔枝共损坏了 600(千克)(答案不唯一);
(元),
答:该公司销售这批荔枝每千克定为10.7元才不亏本.
23.解:(1)调查人数为 (人),
“命中4 次”所对应的圆心角度数为
故答案为:
“命中5 次”的人数为40-10-12-15=3(人),
补全条形统计图如图:
(2)原命中结果的平均数为
∵一名队员新加入篮球队,结果五次定点投篮后,把命中结果与原命中结果组成一组新数据,发现平均数变小了,∴此队员命中结果的最大值为 3;
(3)若n名队员加入篮球队,命中结果均为3,此时中位数不会变化;
若n名队员加入篮球队,命中结果均大于3,
当中位数为 时,n的值为4;
当命中结果为其他情况时,n的值均大于4.
综上所述,n的最小值为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章综合测试题
时间: 45分钟 满分: 100分
一、选择题(本大题共10小题,每小题3分,共30分)
1.根据某市统计局发布的该市近5年的年度GDP 增长率的有关数据,经济学家评论说,该市近5年的年度GDP 增长率相当平稳,从统计学的角度看,判断“增长率相当平稳”的依据是数据的( )
A.中位数 B.平均数 C.众数 D.方差
2.已知一组数据:-3,6,2,-1,0,4,则这组数据的中位数是 ( )
A. 1 B. C. 0 D. 2
3.若一组数据1,3,4,6,m的平均数为4,则这组数据的中位数和众数分别是 ( )
A. 4,4 B. 4,6 C. 3,6 D. 3,4
4.方差是刻画一组数据波动大小的量,对于一组数据可用如下算式计算方差: 其中“3”是这组数据的 ( )
A.最小值 B.平均数 C.众数 D.中位数
5.2022北京冬奥会期间,为了表达对志愿者工作的支持,某班学生积极参加捐款活动,该班50名学生的捐款统计情况如表:
金额/元 5 10 20 50 100
人数 6 17 14 8 5
则他们捐款金额的众数与中位数是 ( )
A. 20,10 B. 17,14 C. 10,20 D. 17,20
6.某校举办读书分享大赛活动,最终有13名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖3名.某参赛同学知道自己的分数后,要判断自己能否获奖,他需要知道这13名学生成绩的 ( )
A.中位数 B.平均数 C.众数 D.方差
7.小颖姐姐今年大学毕业了,她去一家公司参加招聘文员测试,公司对应试者进行了笔试和面试测试,再按笔试占60%、面试占40%计算应试者的总成绩,已知小颖姐姐笔试得85分、面试得75分,则她的总成绩为 ( )
A. 79分 B. 80分 C. 81分 D. 82分
8.甲、乙两位同学连续五次的数学成绩如图所示,下列说法正确的是 ( )
D.无法比较与的大小
9.一组数据:3,4,4,5.如果再添加一个数据4,那么会发生变化的统计量是 ( )
A.平均数 B.中位数 C.众数 D.方差
10.已知数据;数据B:.若数据A 的方差比数据B的方差小,则x的值可能是 ( )
A. 5 B. 4 C. 2 D. 0
二、填空题(本大题共6小题,每小题3分,共18分)
11.若一组数据的极差为9,则x的值是_________.
12.甲、乙两队参加“传承红色基因,推动绿色发展”为主题的合唱比赛,每队均由20名队员组成.其中两队队员的平均身高为 身高的方差分别为 如果单从队员的身高考虑,你认为演出形象效果较好的是_________队.
13.根据第七次全国人口普查,华东A,B,C,D,E,F六省60岁及以上人口占比情况如图所示,这六省60岁及以上人口占比的中位数是_________.
14.某小组6名学生的平均身高a cm,规定超a cm 的部分记为正数,不a cm的部分记为负数,他们的身高与平均身高的差值情况记录如表:
学生序号 1 2 3 4 5 6
身高差值(cm) +2 x +3 -1 -4 -1
据此判断,2号学生的身高为________ cm.(用含a的代数式表示)
15.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为_________.
16.在5个正整数a,b,c,d,e中,中位数是4,唯一的众数是6,则这5个数的和的最大值是__________.
三、解答题(本大题共7 小题,共52分)
17.(6分)某校决定从八年级两个班中选择一个班作为市级先进班级的候选班,现对这两个班进行综合素质考评,如表是这两个班五项考评的得分表(单位:分,每项满分为10分).
班级 道德行为/分 学习成绩/分 艺术获奖/分 劳动卫生/分 校运动会/分
八年级(1)班 9 8 7 9 7
八年级(2)班 8 9 8 9 8
如果将道德行为、学习成绩、艺术获奖、劳动卫生、校运动会五项得分按2:3:1:3:1的比例确定各班的最终得分,那么该校会选择哪个班作为市级先进班级的候选班
18.(6分)某公司随机抽取一名职工,统计了他一个月(30天)每天上班通勤费用,
通勤费用(元/天) 0元 4元 8元 36元
天数(天) 8 12 6 4
(1)该名职工上班通勤费用的中位数是_________,众数是_________;
(2)若该公司每天补贴该职工上班通勤费用6元,请你利用统计知识判断该职工是否还需自行补充上班通勤费用
19.(6分)某校八年级开展了“好书伴成长”读书活动,要求260名学生每人每学期至少阅读4本~7本课外读物,学期结束后随机抽查了若干名学生每人阅读课外书的数量,并分为四种类型,A:4本;B:5本;C:6本;D:7本,将各类的人数绘制成如图所示的扇形统计图和条形统计图.
(1)求这次被调查学生的人数;
(2)写出被调查学生每人阅读课外书数量的众数、中位数;
(3)求被调查学生每人阅读课外书数量的平均数,并估计这260名学生阅读课外书的总数.
20.(8分)某校团委12月份举办七、八年级以“我做守法好公民”为主题的知识竞赛,七、八年级参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了下列不完整的统计图表.
七年级成绩统计表
分数(分) 人数(人)
70 7
80 n
90 1
100 8
(1)七年级成绩统计表中n的值为_________;图1中,“100分”所在扇形的圆心角度数为________;
(2)八年级成绩的中位数为_________分;七年级成绩的平均分为________分;
(3)经计算知 请你根据这两个数据,对七、八年级成绩作出合理评价.
21.(8分)为比较营养液A 和营养液B对某种小西红柿产量的影响,甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验.甲组使用营养液A,乙组使用营养液B.将每株的产量记录整理,并绘制了下列两个条形图.
回答下列问题:
(1)甲组产量的众数为__________,乙组产量的中位数为_________;
(2)已知 则
(3)为了使产量更稳定,则应选择营养液_________;(填“A”或“B”)
(4)产量30个及以上为秧苗长势良好,现在选用第(3)问推荐的营养液培育100株秧苗,请估计长势良好的大约有多少株.
22.(8分)某水果公司以10元/ kg的成本价新进2 000 箱荔枝,每箱质量5kg,在出售荔枝前,需要去掉损坏的荔枝,现随机抽取20箱,去掉损坏荔枝后称得每箱的质量(单位: kg)如下:
4.7 4.8 4.6 4.5 4.8 4.9 4.8 4.7 4.8 4.7
4.8 4.9 4.7 4.8 4.5 4.7 4.7 4.9 4.7 5.0
整理数据:
质量(kg) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b C
(1)直接写出上述表格中a,b,c的值;
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这2 000 箱荔枝共损坏了多少千克
(3)根据(2)中的结果,求该公司销售这批荔枝每千克定为多少元才不亏本(结果保留一位小数)
23.(10分)某篮球队,全员进行定点投篮训练,每人投五次,训练结束后,发现命中的结果只有2次、3次、4次、5次,并把结果制成了如图1,图2所示不完整的条形统计图和扇形统计图.
(1)“命中4次”所在扇形的圆心角是________;请将条形统计图补充完整;
(2)若有一名队员新加入篮球队,经过五次定点投篮后,把命中结果与原命中结果组成一组新数据,发现平均数变小,求此队员命中结果的最大值;
(3)若有n名队员新加入篮球队,经过五次定点投篮后,把命中结果与原命中结果组成一组新数据,发现中位数发生了变化,求n的最小值.
参考答案
1. D 2. A 3. B 4. B 5. C 6. A 7. C 8. B 9. D 10. C
11. -4 或8 12. 乙 13. 18.75% 14. (a+1) 15. 1 16. 21
17.解:八年级(1)班的最终得分为 (分),
八年级(2)班的最终得分为 (分),
∴该校会选择八年级(2)班作为市级先进班级的候选班.
18.解:(1)将这30天的该名职工上班通勤费用从小到大排列,第15 和第 16 两个数都是4元,因此中位数是4元,这30天的该名职工上班通勤费用出现次数最多的是4元,共出现12次,因此众数是4元,
故答案为:4元,4元;
(2)需要,理由如下:
这30天的该名职工上班通勤费用的平均数为 (元),
∵6<8,∴该职工还需要自行补充上班通勤费用.
19.解: (名).
答:这次被调查学生有20名;
(2)∵读了5本课外书的有8人,最多,
∴被调查学生阅读课外书数量的众数为5本;
∵共有 20人,∴中位数是第10人和第11人的平均数,
∴被调查学生阅读课外书数量的中位数为 (本);
(3)平均数为 (本);
估计这260名学生阅读课外书的总数约为 (本).
20.解:(1)参赛的人数为( (人),
七年级成绩统计表中
图1中,“100分”所在扇形的圆心角度数为
故答案为: 4,90°;
(2)∵一共有20人参赛,第10个数为90,第11个数为90,
∴八年级成绩的中位数为
七年级成绩的平均分为
故答案为:90,85;
∴八年级20名同学的成绩比较整齐.
21.解:(1)由条形统计图,得甲组产量的众数为30个,
乙组产量第5个数是31,第6个数是32,
乙组产量的中位数为 (个).
故答案为:30个,31.5个;
故答案为: 6.84;
(3)由(2),得
∴甲组方差较小,产量的波动较小,产量更稳定,
所以应选择营养液 A;
故答案为:A;
(4)估计长势良好的大约有 70(株).
答:估计长势良好的大约有70株.
22.解:(
分析数据:样本中,4.7出现的次数最多,故众数b为4.7;
将数据从小到大排列,找最中间的两个数为4.7,4.8,故中位数
综上所述,
(2)选择众数4.7,
这2000箱荔枝共损坏了 600(千克)(答案不唯一);
(元),
答:该公司销售这批荔枝每千克定为10.7元才不亏本.
23.解:(1)调查人数为 (人),
“命中4 次”所对应的圆心角度数为
故答案为:
“命中5 次”的人数为40-10-12-15=3(人),
补全条形统计图如图:
(2)原命中结果的平均数为
∵一名队员新加入篮球队,结果五次定点投篮后,把命中结果与原命中结果组成一组新数据,发现平均数变小了,∴此队员命中结果的最大值为 3;
(3)若n名队员加入篮球队,命中结果均为3,此时中位数不会变化;
若n名队员加入篮球队,命中结果均大于3,
当中位数为 时,n的值为4;
当命中结果为其他情况时,n的值均大于4.
综上所述,n的最小值为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
