22.3 实际问题与二次函数 第1课时 课件(共21张PPT)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数 第1课时 课件(共21张PPT)2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 984.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
22.3 实际问题与二次函数
第1课时
第二十二章 二次函数
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)y=x2-4x-5; (配方法) (2)y=-x2-3x+4.(公式法)
解:(1)开口方向:向上;对称轴:x=2;
顶点坐标:(2,-9);最小值:-9;
(2)开口方向:向下;对称轴:x= ;
顶点坐标:( , );
最大值: .
二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由a及自变量的取值范围决定.
1.分析实际问题中变量之间的二次函数关系.(难点)
2.能应用二次函数的性质解决图形中最大面积问题,
商品销售过程中的最大利润问题.(重点)
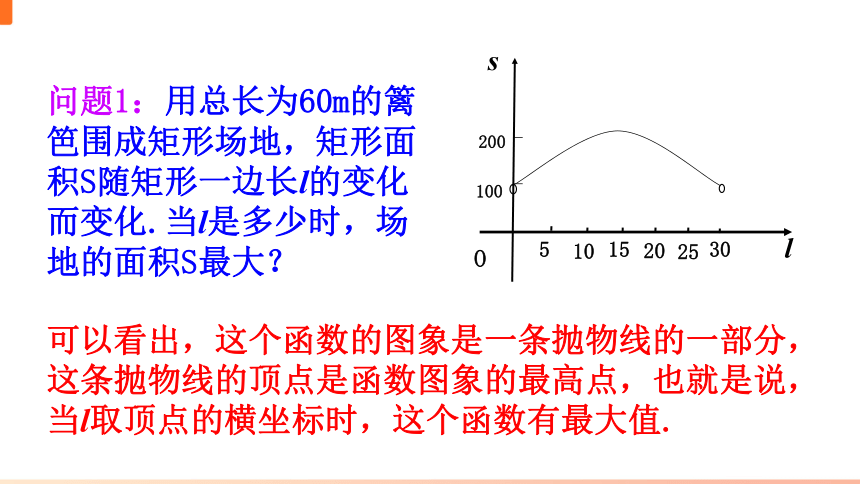
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随
矩形一边长l的变化而变化.当l是多少时,场地的
面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l值.
矩形场地的周长是60m,一边长为l,则另一边长为 m.场地的面积: ,
(0S=l(30-l)
即S=-l2+30l
请同学们画出此函数的图象
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.
5
10
15
20
25
30
100
200
l
s
O
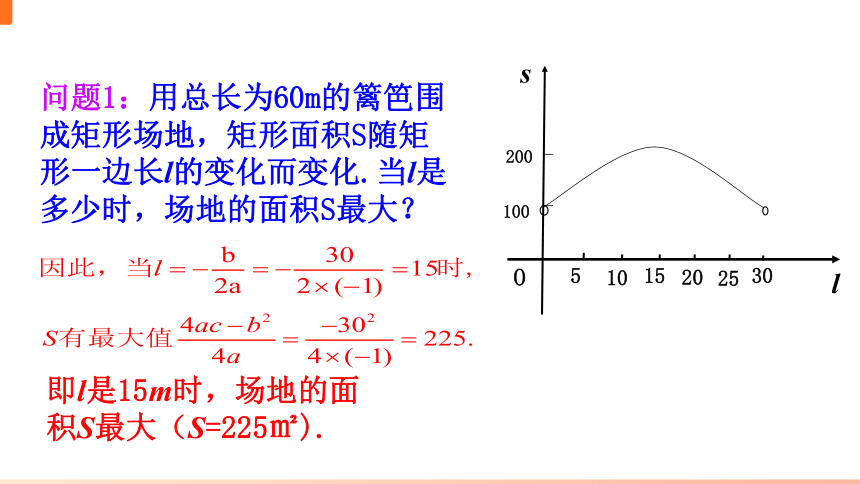
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
5
10
15
20
25
30
100
200
l
s
即l是15m时,场地的面积S最大(S=225㎡).
O
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
一般地,因为抛物线y=ax2+bx+c的顶点是最低
(高)点,所以当 时,二次函数y=ax2+bx+c有
最小(大)值 .
结论:
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
请同学们思考:
(1)题目中有几种调整价格的方法?
(2)题目涉及哪些变量?哪一个量是自变量?哪些量随之发生
了变化?
分析:
调整价格包括涨价和降价两种情况.
①先来看涨价的情况:设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y随x变化的函数解析式.
涨价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
【解析】设每件涨价x元,则y=(60+x-40)(300-10x),
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6 250.
怎样确定x的取值范围
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元.
也可以这样求最值:
②在降价的情况下,最大利润是多少?请你参考①的过程得出答案.
【解析】设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润:
y=(300+20x)(60-40-x)
=-20(x -5x+6.25)+6125
=-20(x-2.5) +6125
∴x=2.5时,y最大值=6125.
怎样确定x的取值范围
(0<x<20)
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最大值或最小值.
用二次函数解决最值问题的一般步骤:
【归纳】
抽象
二次函数问题
运用
问题的解决
实际问题
1. 某小区在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙, 另三边用总长为40m的栅栏围住.设绿化带的边长BC为xm,绿化带的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量的取值范围.
25 m
D
A
C
B
(2)当x为何值时,满足条件的绿化带的面积最大?
2.(2020·湖北中考)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市” 期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为 ____元.
【解析】设每顶头盔的售价为x元,获得的利润为w元 w= (x-50) [200+ ( 80-x ) 20]=-20 (x-70) 2 +8000
当x=70时,w取得最大值,此时w=8000 故答案为:70
70
3.(2020·葫芦岛中考)小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周的销售量y(本)与销售单价x (元)之间满足一次函数关系,三对对应值如下表:
(1)求y与x之间的函数关系式; (2)通过与其他网店对比,小红将这款笔记本的单价定为x元(12≤x≤15, 且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元
【解析】(1)设y与x之间的函数关系式是y=kx+b( k≠0)
即y与x之间的函数关系式为y=-50x+1100
(2)由题意可得:W= (x-10)y=(x-10) (-50x+1100)
=-50(x-16)2+ 1800 ∵a=-50<0
∴w有最大值 当x<16时,w随x的增大而增大 当x=15时,x有最大值,此时w=-50( 15-16) 2+ 1800=1750
答:销售单价为15元时每周获利最大,最大利润是1750元.
一个人有了远大的理想,就是在最艰苦困难的时候,也会感到幸福.
——佚名
22.3 实际问题与二次函数
第1课时
第二十二章 二次函数
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)y=x2-4x-5; (配方法) (2)y=-x2-3x+4.(公式法)
解:(1)开口方向:向上;对称轴:x=2;
顶点坐标:(2,-9);最小值:-9;
(2)开口方向:向下;对称轴:x= ;
顶点坐标:( , );
最大值: .
二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由a及自变量的取值范围决定.
1.分析实际问题中变量之间的二次函数关系.(难点)
2.能应用二次函数的性质解决图形中最大面积问题,
商品销售过程中的最大利润问题.(重点)
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随
矩形一边长l的变化而变化.当l是多少时,场地的
面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l值.
矩形场地的周长是60m,一边长为l,则另一边长为 m.场地的面积: ,
(0
即S=-l2+30l
请同学们画出此函数的图象
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.
5
10
15
20
25
30
100
200
l
s
O
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
5
10
15
20
25
30
100
200
l
s
即l是15m时,场地的面积S最大(S=225㎡).
O
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
一般地,因为抛物线y=ax2+bx+c的顶点是最低
(高)点,所以当 时,二次函数y=ax2+bx+c有
最小(大)值 .
结论:
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
请同学们思考:
(1)题目中有几种调整价格的方法?
(2)题目涉及哪些变量?哪一个量是自变量?哪些量随之发生
了变化?
分析:
调整价格包括涨价和降价两种情况.
①先来看涨价的情况:设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y随x变化的函数解析式.
涨价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
【解析】设每件涨价x元,则y=(60+x-40)(300-10x),
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6 250.
怎样确定x的取值范围
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元.
也可以这样求最值:
②在降价的情况下,最大利润是多少?请你参考①的过程得出答案.
【解析】设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润:
y=(300+20x)(60-40-x)
=-20(x -5x+6.25)+6125
=-20(x-2.5) +6125
∴x=2.5时,y最大值=6125.
怎样确定x的取值范围
(0<x<20)
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最大值或最小值.
用二次函数解决最值问题的一般步骤:
【归纳】
抽象
二次函数问题
运用
问题的解决
实际问题
1. 某小区在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙, 另三边用总长为40m的栅栏围住.设绿化带的边长BC为xm,绿化带的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量的取值范围.
25 m
D
A
C
B
(2)当x为何值时,满足条件的绿化带的面积最大?
2.(2020·湖北中考)某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市” 期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为 ____元.
【解析】设每顶头盔的售价为x元,获得的利润为w元 w= (x-50) [200+ ( 80-x ) 20]=-20 (x-70) 2 +8000
当x=70时,w取得最大值,此时w=8000 故答案为:70
70
3.(2020·葫芦岛中考)小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周的销售量y(本)与销售单价x (元)之间满足一次函数关系,三对对应值如下表:
(1)求y与x之间的函数关系式; (2)通过与其他网店对比,小红将这款笔记本的单价定为x元(12≤x≤15, 且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元
【解析】(1)设y与x之间的函数关系式是y=kx+b( k≠0)
即y与x之间的函数关系式为y=-50x+1100
(2)由题意可得:W= (x-10)y=(x-10) (-50x+1100)
=-50(x-16)2+ 1800 ∵a=-50<0
∴w有最大值 当x<16时,w随x的增大而增大 当x=15时,x有最大值,此时w=-50( 15-16) 2+ 1800=1750
答:销售单价为15元时每周获利最大,最大利润是1750元.
一个人有了远大的理想,就是在最艰苦困难的时候,也会感到幸福.
——佚名
同课章节目录
