23.1 图形的旋转 课件(共17张PPT) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 23.1 图形的旋转 课件(共17张PPT) 2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 793.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 18:48:32 | ||
图片预览




文档简介
(共17张PPT)
23.1 图形的旋转
第二十三章 旋转
【欣赏】
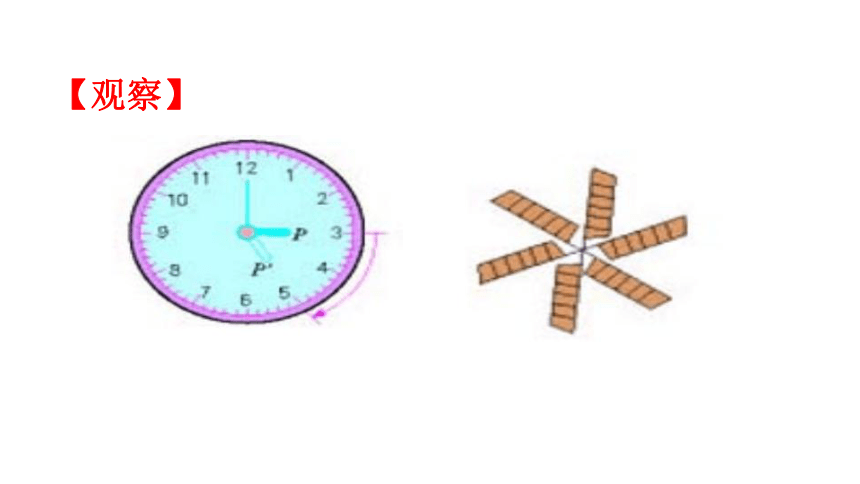
【观察】
1.了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及应用它们解决一些实际问题.
2.通过复习平移、轴对称的有关概念及性质,从生活中的数学开始,经历观察,产生概念,应用概念解决一些实际问题.
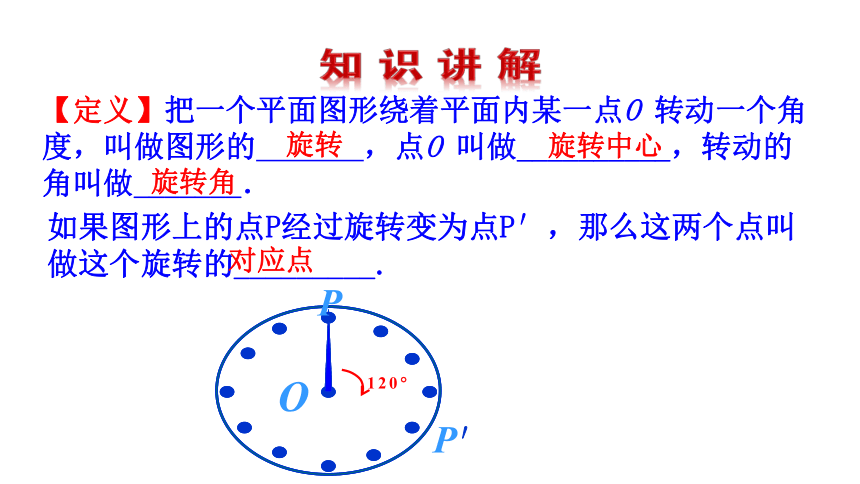
【定义】把一个平面图形绕着平面内某一点O 转动一个角
度,叫做图形的 ,点O 叫做__________,转动的
角叫做_______.
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的_________.
旋转
旋转中心
旋转角
对应点
O
P′
P
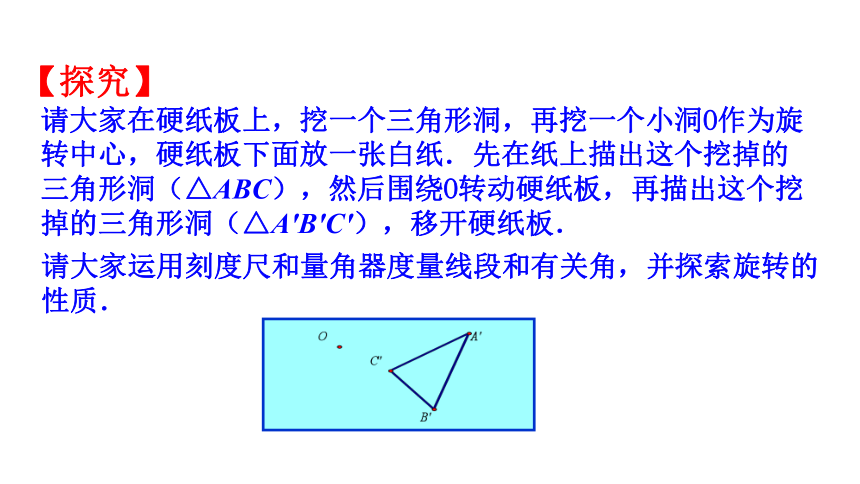
请大家在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形洞(△ABC),然后围绕O转动硬纸板,再描出这个挖掉的三角形洞(△A′B′C′),移开硬纸板.
请大家运用刻度尺和量角器度量线段和有关角,并探索旋转的性质.
【探究】
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
旋转的性质:
【归纳】
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
【例题】
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以∠ABE′=∠ADE=90°,BE′=DE .
【解析】因为点A是旋转中心
所以它的对应点是它本身.
在正方形ABCD中,AD=AB,
∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形.
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
1. (2020·镇江中考) O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转 后能与原来的图案互相重合.
72°
【跟踪训练】
【解析】连接OA,OE,则这个图形至少旋转
∠AOE才能与原图象重合
∠AOE=360°÷5=72° 故答案为:72 °
2.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?
答案:4次
通过本课时的学习,需要我们掌握:
1.旋转及其旋转中心、旋转角的概念.
2.旋转的对应点及它们的应用.
1.下列现象中属于旋转的有( )个.
①地下水位逐年下降;②传送带的移动;
③方向盘的转动; ④水龙头的转动;
⑤钟摆的运动; ⑥荡秋千.
A.2 B.3 C.4 D.5
C
2. 如图,在5×5的网格中,每个小正方形的边长均为1,点
A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°,
得到△OA′B′,A,B的对应点分别为A′,B′,则A,
B′之间的距离为( )
A.2 B.5 C. D.
【解析】如图,由旋转的性质作出△OA′B′ ,连接AB ′,
∵每个小正方形的边长均为1, AB ′=
C
3. 如图,把这个“十字星”形图绕其中心点O旋转,当至少旋转 度后,所得图形与原图形重合.
90
新的术语是让读者接着研究那摆在他们面前的奇妙难尽的东西,使科学获得了巨大的进展.
——柯西
23.1 图形的旋转
第二十三章 旋转
【欣赏】
【观察】
1.了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及应用它们解决一些实际问题.
2.通过复习平移、轴对称的有关概念及性质,从生活中的数学开始,经历观察,产生概念,应用概念解决一些实际问题.
【定义】把一个平面图形绕着平面内某一点O 转动一个角
度,叫做图形的 ,点O 叫做__________,转动的
角叫做_______.
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的_________.
旋转
旋转中心
旋转角
对应点
O
P′
P
请大家在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形洞(△ABC),然后围绕O转动硬纸板,再描出这个挖掉的三角形洞(△A′B′C′),移开硬纸板.
请大家运用刻度尺和量角器度量线段和有关角,并探索旋转的性质.
【探究】
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前、后的图形全等.
对应点到旋转中心的距离相等.
旋转的性质:
【归纳】
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
【例题】
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以∠ABE′=∠ADE=90°,BE′=DE .
【解析】因为点A是旋转中心
所以它的对应点是它本身.
在正方形ABCD中,AD=AB,
∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形.
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
1. (2020·镇江中考) O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转 后能与原来的图案互相重合.
72°
【跟踪训练】
【解析】连接OA,OE,则这个图形至少旋转
∠AOE才能与原图象重合
∠AOE=360°÷5=72° 故答案为:72 °
2.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?
答案:4次
通过本课时的学习,需要我们掌握:
1.旋转及其旋转中心、旋转角的概念.
2.旋转的对应点及它们的应用.
1.下列现象中属于旋转的有( )个.
①地下水位逐年下降;②传送带的移动;
③方向盘的转动; ④水龙头的转动;
⑤钟摆的运动; ⑥荡秋千.
A.2 B.3 C.4 D.5
C
2. 如图,在5×5的网格中,每个小正方形的边长均为1,点
A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°,
得到△OA′B′,A,B的对应点分别为A′,B′,则A,
B′之间的距离为( )
A.2 B.5 C. D.
【解析】如图,由旋转的性质作出△OA′B′ ,连接AB ′,
∵每个小正方形的边长均为1, AB ′=
C
3. 如图,把这个“十字星”形图绕其中心点O旋转,当至少旋转 度后,所得图形与原图形重合.
90
新的术语是让读者接着研究那摆在他们面前的奇妙难尽的东西,使科学获得了巨大的进展.
——柯西
同课章节目录
