23.2.3 关于原点对称的点的坐标 课件(共17张PPT) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 课件(共17张PPT) 2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 942.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
23.2 中心对称
23.2.3 关于原点对称的点的坐标
第二十三章 旋转
1.中心对称的两个图形有何性质?
(2)中心对称的两个图形是全等图形.
(1)中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心平分.
2.在下列图形中,是中心对称图形的是( )
C
3.下列美丽的图案,既是轴对称图形又是中心对称
图形的个数是( )
A.1 B.2 C.3 D.4
C
1.探索平面直角坐标系下点关于x轴,y轴,原点的对称点的坐标特征.
2.掌握关于原点对称的两个点的横纵坐标之间的关系,并灵活运用.
1
2
3
4
5
-4
-3
-2
-1
·
O
x
P(-3,2)
A(-3,- 2 )
你能说出点P关于x轴对称点的坐标吗?
3
1
4
2
5
-2
-4
-1
-3
y
思考:关于x轴对称的点的坐标具有怎样的关系
结论:在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
1
2
3
4
5
-4
-3
-2
-1
·
O
x
B(3,2)
P(-3,2)
你能说出点P关于y轴对称点的坐标吗?
3
1
4
2
5
-2
-4
-1
-3
y
思考:关于y轴对称的点的坐标具有怎样的关系
结论:在直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数
1
2
3
4
5
-4
-3
-2
-1
·
O
x
B(3,2)
C(3,-2)
P(-3,2)
A(-3,- 2 )
3
1
4
2
5
-2
-4
-1
-3
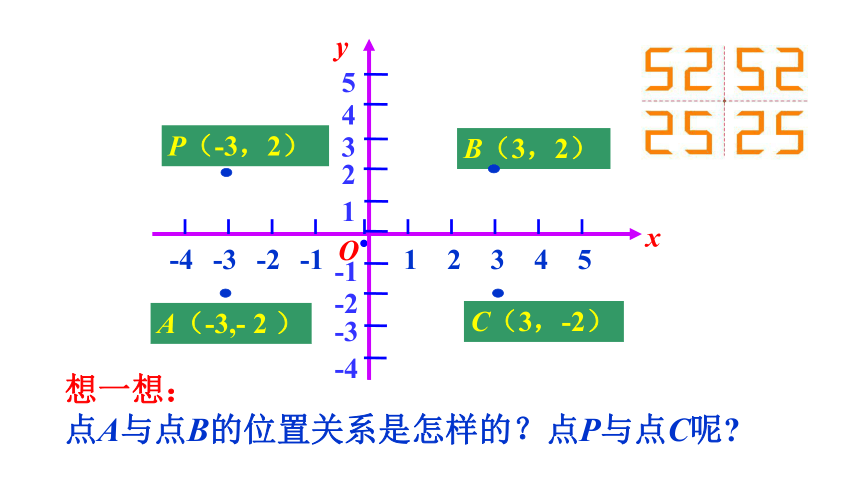
想一想:
点A与点B的位置关系是怎样的?点P与点C呢
y
关于原点对称的点的坐标
A′
问题:如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
记作A′ ( -2,-1 )
记作A ( 2,1 )
B
B′
△ABO≌△A′B′ O
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
-3
A
B
E
练一练:在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-2)
D
C
(-4,0)
(0,3)
(-2,-1)
(1,-2)
(3,2)
思考:关于原点对称的两个点的坐标之间有什么关系?
横坐标、纵坐标的符号都互为相反数
关于原点对称的点的坐标关系特点
简记为:“关于谁,谁不变,关于原点都改变”.
即:
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
【归纳】
例 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
A
C
B
A′
C′
B′
解:△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点分别为
依次连接A ′B ′ ,B ′
C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的
△ A′B′ C ′ .
【例题】
1.下列各点中哪两个点关于原点O对称?
A(-5,0) B(0,2) C(2,-1) D(2,0)
E(0,5) F(-2,1) G(-2,-1)
2.写出下列各点关于原点的对称点的坐标.
A(3,1) B(-2,3) C(-1,-2) D(2,-3)
A(-3,-1) B(2,-3) C(1,2) D(-2,3)
3.若点A(m,-2),B(1,n)关于原点对称,则m=____,n=____ .
-1
2
【跟踪训练】
通过本课时的学习,需要我们掌握:
1.关于x轴对称的两点,横坐标相同,纵坐标互为
相反数;
2.关于y轴对称的两点,纵坐标相同,横坐标互为
相反数;
3.两个点关于原点对称时,它们的纵横坐标均互为
相反数.
1.(2020·淮安中考)在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A.(2,3) B.(-3,2)
C.(-3,-2) D.(-2,-3)
C
2.(2021 常州模拟)在平面直角坐标系中,点A
(a,2)与点B(6,b)关于原点对称,则ab= .
12
【解析】∵点A(a,2)与点B(6,b)关于原点对称, ∴a=-6,b=-2 ∴ab=12 答案:12.
3.如图,阴影部分组成的图案 ,既是关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),则点M 和点N 的坐标分别是:
M(-1,-3)
N(1,-3)
在学习中要敢于做减法,就是减去前人已经解决的部分,看看还有哪些问题没有解决,需要我们去探索解决.
——华罗庚
23.2 中心对称
23.2.3 关于原点对称的点的坐标
第二十三章 旋转
1.中心对称的两个图形有何性质?
(2)中心对称的两个图形是全等图形.
(1)中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心平分.
2.在下列图形中,是中心对称图形的是( )
C
3.下列美丽的图案,既是轴对称图形又是中心对称
图形的个数是( )
A.1 B.2 C.3 D.4
C
1.探索平面直角坐标系下点关于x轴,y轴,原点的对称点的坐标特征.
2.掌握关于原点对称的两个点的横纵坐标之间的关系,并灵活运用.
1
2
3
4
5
-4
-3
-2
-1
·
O
x
P(-3,2)
A(-3,- 2 )
你能说出点P关于x轴对称点的坐标吗?
3
1
4
2
5
-2
-4
-1
-3
y
思考:关于x轴对称的点的坐标具有怎样的关系
结论:在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
1
2
3
4
5
-4
-3
-2
-1
·
O
x
B(3,2)
P(-3,2)
你能说出点P关于y轴对称点的坐标吗?
3
1
4
2
5
-2
-4
-1
-3
y
思考:关于y轴对称的点的坐标具有怎样的关系
结论:在直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数
1
2
3
4
5
-4
-3
-2
-1
·
O
x
B(3,2)
C(3,-2)
P(-3,2)
A(-3,- 2 )
3
1
4
2
5
-2
-4
-1
-3
想一想:
点A与点B的位置关系是怎样的?点P与点C呢
y
关于原点对称的点的坐标
A′
问题:如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
记作A′ ( -2,-1 )
记作A ( 2,1 )
B
B′
△ABO≌△A′B′ O
x
y
O
-4 -3 -2 -1 1 2 3 4
-1
2
3
4
1
-2
-3
A
B
E
练一练:在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-2)
D
C
(-4,0)
(0,3)
(-2,-1)
(1,-2)
(3,2)
思考:关于原点对称的两个点的坐标之间有什么关系?
横坐标、纵坐标的符号都互为相反数
关于原点对称的点的坐标关系特点
简记为:“关于谁,谁不变,关于原点都改变”.
即:
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
【归纳】
例 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
A
C
B
A′
C′
B′
解:△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点分别为
依次连接A ′B ′ ,B ′
C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的
△ A′B′ C ′ .
【例题】
1.下列各点中哪两个点关于原点O对称?
A(-5,0) B(0,2) C(2,-1) D(2,0)
E(0,5) F(-2,1) G(-2,-1)
2.写出下列各点关于原点的对称点的坐标.
A(3,1) B(-2,3) C(-1,-2) D(2,-3)
A(-3,-1) B(2,-3) C(1,2) D(-2,3)
3.若点A(m,-2),B(1,n)关于原点对称,则m=____,n=____ .
-1
2
【跟踪训练】
通过本课时的学习,需要我们掌握:
1.关于x轴对称的两点,横坐标相同,纵坐标互为
相反数;
2.关于y轴对称的两点,纵坐标相同,横坐标互为
相反数;
3.两个点关于原点对称时,它们的纵横坐标均互为
相反数.
1.(2020·淮安中考)在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A.(2,3) B.(-3,2)
C.(-3,-2) D.(-2,-3)
C
2.(2021 常州模拟)在平面直角坐标系中,点A
(a,2)与点B(6,b)关于原点对称,则ab= .
12
【解析】∵点A(a,2)与点B(6,b)关于原点对称, ∴a=-6,b=-2 ∴ab=12 答案:12.
3.如图,阴影部分组成的图案 ,既是关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),则点M 和点N 的坐标分别是:
M(-1,-3)
N(1,-3)
在学习中要敢于做减法,就是减去前人已经解决的部分,看看还有哪些问题没有解决,需要我们去探索解决.
——华罗庚
同课章节目录
