24.1.2 垂直于弦的直径 课件(共23张PPT) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 24.1.2 垂直于弦的直径 课件(共23张PPT) 2024-2025学年人教版数学九年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 717.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 18:46:01 | ||
图片预览




文档简介
(共23张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
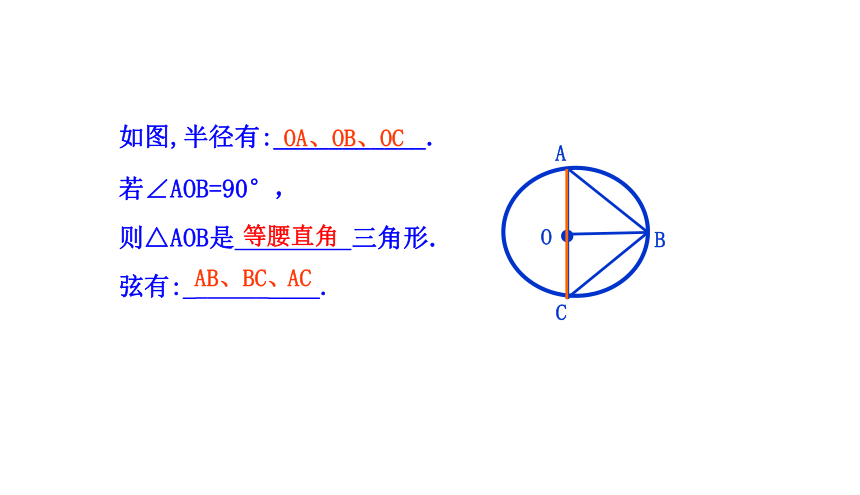
如图,半径有:___________.
O
B
C
A
OA、OB、OC
若∠AOB=90°,
则△AOB是 三角形.
弦有:___________.
AB、BC、
AC
等腰直角
●
O
B
C
A
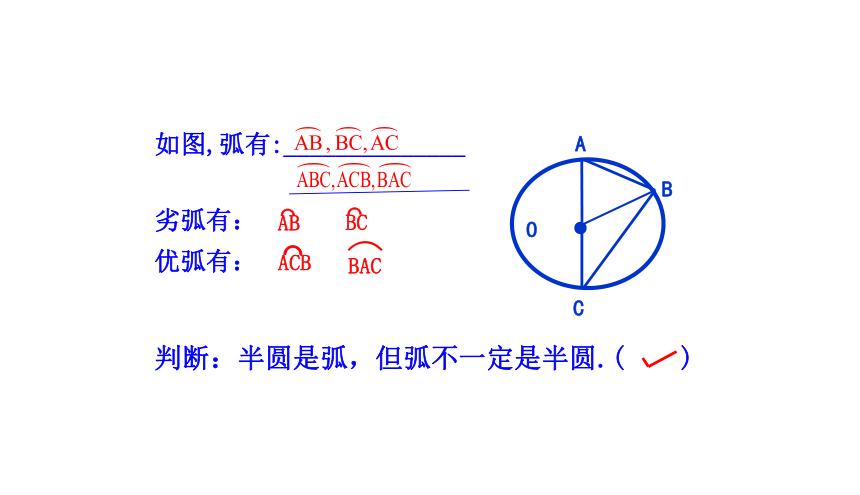
如图,弧有:______________
⌒
AB
⌒
BC
劣弧有:
优弧有:
判断:半圆是弧,但弧不一定是半圆.( )
●
⌒
BAC
⌒
ACB
1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)
3.灵活运用垂径定理解决有关圆的问题.(难点)
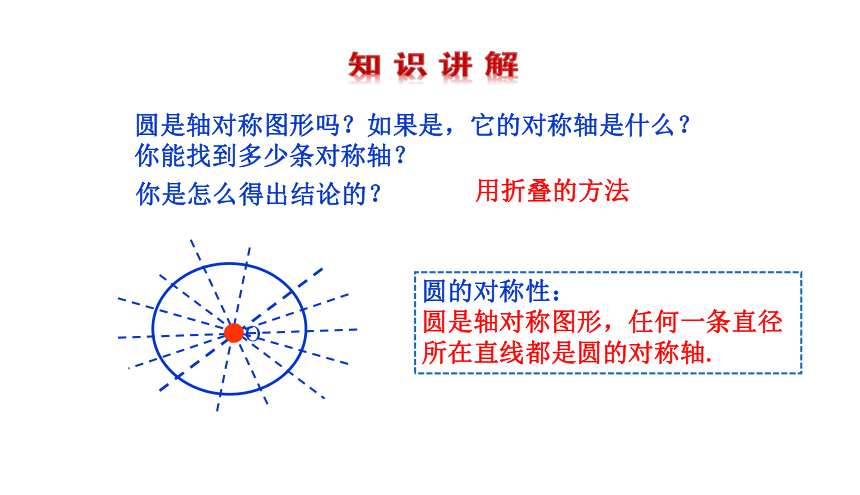
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
你是怎么得出结论的?
圆的对称性: 圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
用折叠的方法
●O
【问题】如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.你能发现图中有哪些相等的线段和劣弧 为什么
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC和BC, AD与BD重合.
⌒
⌒
⌒
⌒
·
O
A
B
D
E
C
垂径定理
·
O
A
B
C
D
E
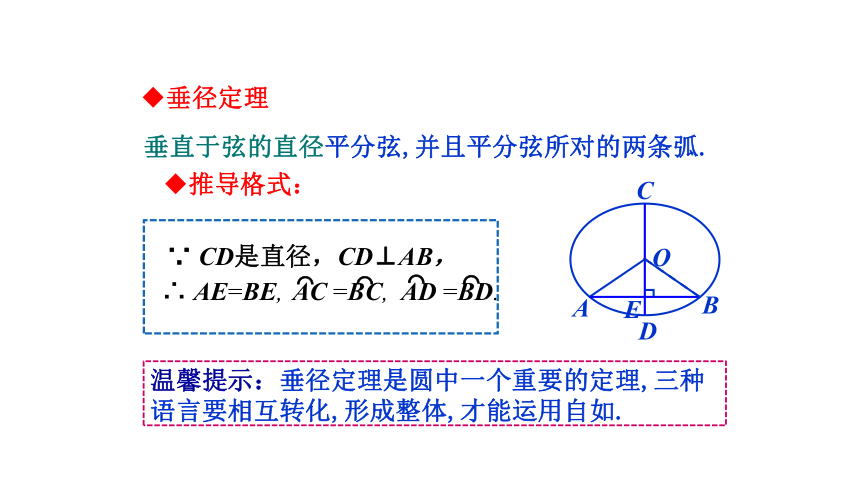
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
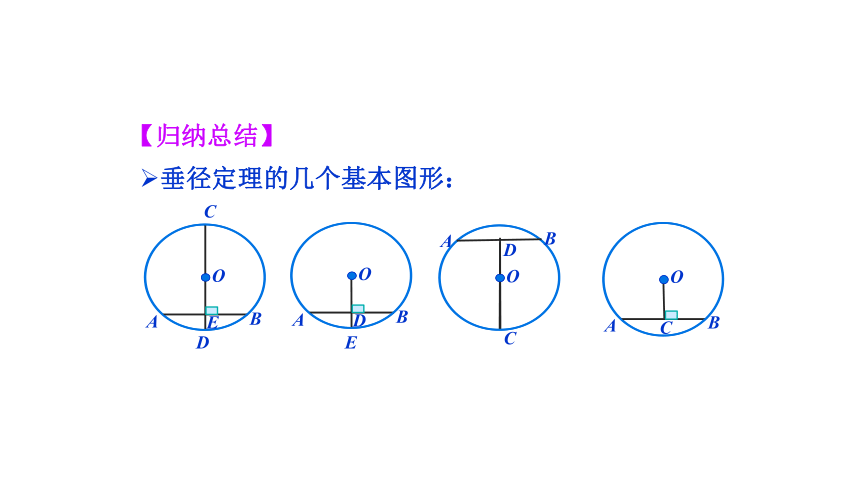
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
【归纳总结】
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心 ;②垂直于弦; ③平分弦;
④平分弦所对的优弧 ; ⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
【思考探索】
D
O
A
B
E
C
举例证明其中一种组合方法
已知:
求证:
① CD是直径
② CD⊥AB,垂足为E
③ AE=BE
④ AC=BC ⑤ AD=BD
⌒
⌒
⌒
⌒
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
⌒
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
(2)由垂径定理可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
⌒
⌒
【证明举例】
·
O
A
B
C
D
E
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
【例1】如图,已知在圆O中,弦AB的
长为8㎝,圆心O到AB的距离为3㎝,
求圆O的半径.
E
O
A
B
【解析】根据题意,得AE=4cm ,OE⊥AB,OE=3cm.
在Rt△OEA中,根据勾股定理,得AO2=OE2+AE2=32+42=25,AO=5cm.
【例题】
变式1:AC,BD有什么关系?
变式2:AC=BD依然成立吗?
变式3:EA=____, EC=_____.
FD
FB
变式4:______,AC=BD.
OA=OB
变式5:______,AC=BD.
OC=OD
【试一试】
【归纳】
作垂直于弦的线段,构造由半径、弦的一半、弦心距为三边的直角三角形,然后用勾股定理解决问题.
E
O
A
B
如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm.
·
O
A
B
E
解析:连接OA,
∵ OE⊥AB,
∴ AB=16cm.
16
cm
【跟踪训练】
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
1.(南通 中考)已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 cm.
12
【解析】如图,作OC⊥AB于C,连接OA, 则AC=BC= AB=5, 在Rt△OAC中,OC= =12, 所以圆心O到AB的距离为12cm. 故答案为12.
2.(滨州 中考)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6 B.9 C.12 D.15
【解析】如图所示:连接OD ∵直径AB=15
∴BO=7.5 ∵OC:OB=3:5
∴CO=4.5 ∴ ∴DE=2DC=12.
C
【解析】连接OB,先由垂径定理得AD=BD= AB=3,则
CD=AD-AC=1,再由勾股定理求出OD= ,然后由勾股定理求出OB
即可.
3.(2021 杭州期末)如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
连接OB,设AB与MN交于点D,如图所示: ∵AC=2,BC=4 ∴AB=AC+BC=6 ∵AB⊥MN ∴AD=BD= AB=3,∠ODC=∠ODB=90° ∴CD=AD-AC=1, ∴ ∴ 即⊙O的半径为 .
要利用时间,思考一下一天之中做了些什么,是 “正号”还是“负号”,倘若是“正号”,则进步;倘若是“负号”,就得吸取教训,采取措施.
——季米特洛夫
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
如图,半径有:___________.
O
B
C
A
OA、OB、OC
若∠AOB=90°,
则△AOB是 三角形.
弦有:___________.
AB、BC、
AC
等腰直角
●
O
B
C
A
如图,弧有:______________
⌒
AB
⌒
BC
劣弧有:
优弧有:
判断:半圆是弧,但弧不一定是半圆.( )
●
⌒
BAC
⌒
ACB
1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)
3.灵活运用垂径定理解决有关圆的问题.(难点)
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
你是怎么得出结论的?
圆的对称性: 圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
用折叠的方法
●O
【问题】如图,AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.你能发现图中有哪些相等的线段和劣弧 为什么
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC和BC, AD与BD重合.
⌒
⌒
⌒
⌒
·
O
A
B
D
E
C
垂径定理
·
O
A
B
C
D
E
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
温馨提示:垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
【归纳总结】
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心 ;②垂直于弦; ③平分弦;
④平分弦所对的优弧 ; ⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
【思考探索】
D
O
A
B
E
C
举例证明其中一种组合方法
已知:
求证:
① CD是直径
② CD⊥AB,垂足为E
③ AE=BE
④ AC=BC ⑤ AD=BD
⌒
⌒
⌒
⌒
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
⌒
AC与BC相等吗? AD与BD相等吗?为什么?
⌒
(2)由垂径定理可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
⌒
⌒
【证明举例】
·
O
A
B
C
D
E
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
【例1】如图,已知在圆O中,弦AB的
长为8㎝,圆心O到AB的距离为3㎝,
求圆O的半径.
E
O
A
B
【解析】根据题意,得AE=4cm ,OE⊥AB,OE=3cm.
在Rt△OEA中,根据勾股定理,得AO2=OE2+AE2=32+42=25,AO=5cm.
【例题】
变式1:AC,BD有什么关系?
变式2:AC=BD依然成立吗?
变式3:EA=____, EC=_____.
FD
FB
变式4:______,AC=BD.
OA=OB
变式5:______,AC=BD.
OC=OD
【试一试】
【归纳】
作垂直于弦的线段,构造由半径、弦的一半、弦心距为三边的直角三角形,然后用勾股定理解决问题.
E
O
A
B
如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm.
·
O
A
B
E
解析:连接OA,
∵ OE⊥AB,
∴ AB=16cm.
16
cm
【跟踪训练】
垂径定理
内容
推论
辅助线
一条直线满足:①过圆心;②垂直于弦; ③平分弦(不是直径); ④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论(“知二推三”)
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作弦心距
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
1.(南通 中考)已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 cm.
12
【解析】如图,作OC⊥AB于C,连接OA, 则AC=BC= AB=5, 在Rt△OAC中,OC= =12, 所以圆心O到AB的距离为12cm. 故答案为12.
2.(滨州 中考)在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6 B.9 C.12 D.15
【解析】如图所示:连接OD ∵直径AB=15
∴BO=7.5 ∵OC:OB=3:5
∴CO=4.5 ∴ ∴DE=2DC=12.
C
【解析】连接OB,先由垂径定理得AD=BD= AB=3,则
CD=AD-AC=1,再由勾股定理求出OD= ,然后由勾股定理求出OB
即可.
3.(2021 杭州期末)如图,已知MN是⊙O的直径,AB是⊙O的弦,AB⊥MN,点C在线段AB上,OC=AC=2,BC=4,求⊙O的半径.
连接OB,设AB与MN交于点D,如图所示: ∵AC=2,BC=4 ∴AB=AC+BC=6 ∵AB⊥MN ∴AD=BD= AB=3,∠ODC=∠ODB=90° ∴CD=AD-AC=1, ∴ ∴ 即⊙O的半径为 .
要利用时间,思考一下一天之中做了些什么,是 “正号”还是“负号”,倘若是“正号”,则进步;倘若是“负号”,就得吸取教训,采取措施.
——季米特洛夫
同课章节目录
