24.1.4 圆周角 课件(共26张PPT) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 24.1.4 圆周角 课件(共26张PPT) 2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 811.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
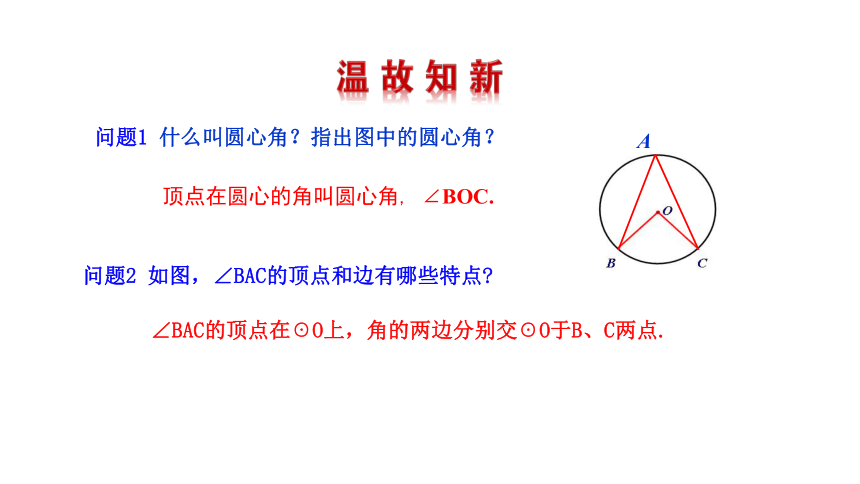
问题1 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图,∠BAC的顶点和边有哪些特点
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
1.理解圆周角的概念,掌握圆周角的定理的内容及简单应用.
2.掌握圆周角的定理的推论及简单应用.
3.了解圆内接多边形的有关概念.
4.掌握圆内接四边形的性质并灵活应用.
.
O
B
C
A
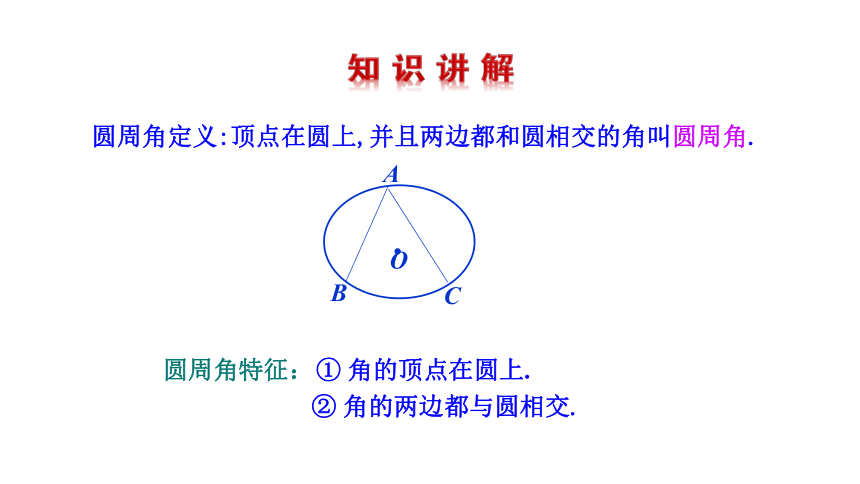
圆周角特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
·
C
O
A
B
·
C
O
B
A
·
C
O
B
·
C
O
B
A
A
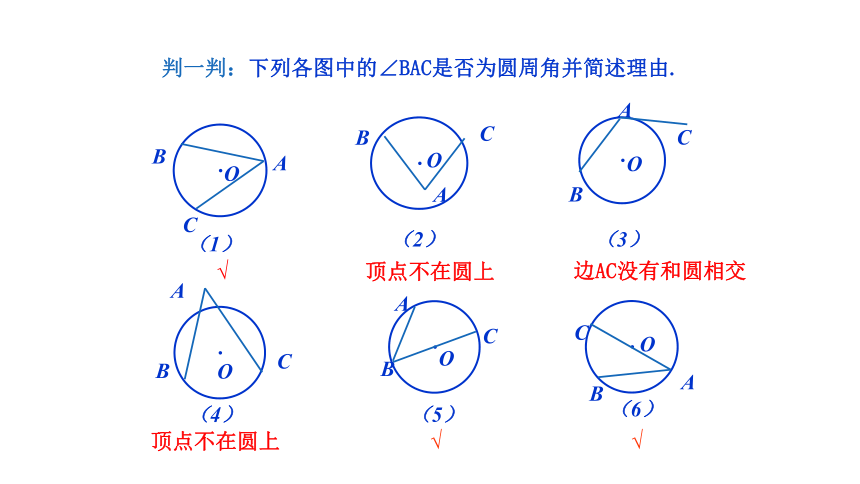
判一判:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
O
·
C
A
B
B
C
A
·
O
(4)
● O
A
B
C
● O
A
B
C
●O
A
B
C
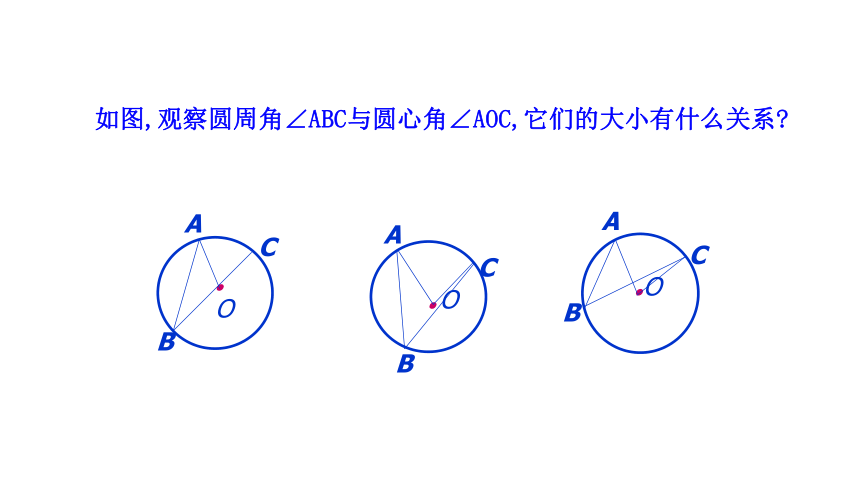
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系
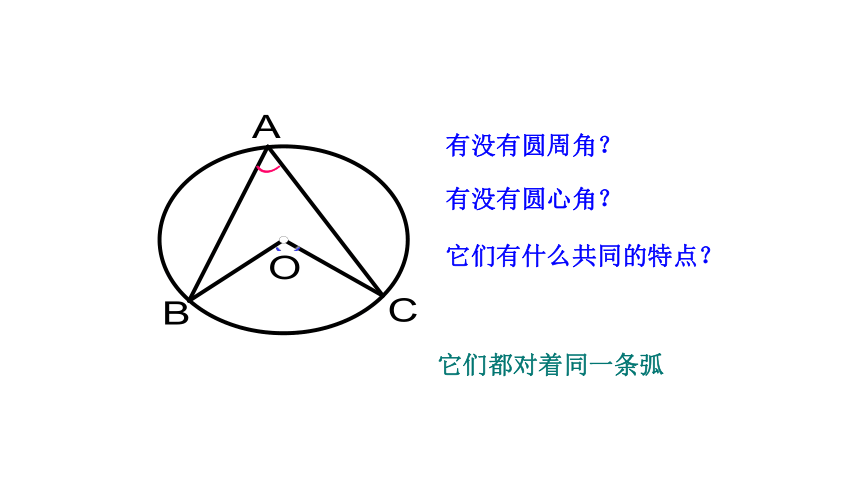
有没有圆周角?
有没有圆心角?
它们有什么共同的特点?
它们都对着同一条弧
⌒
⌒
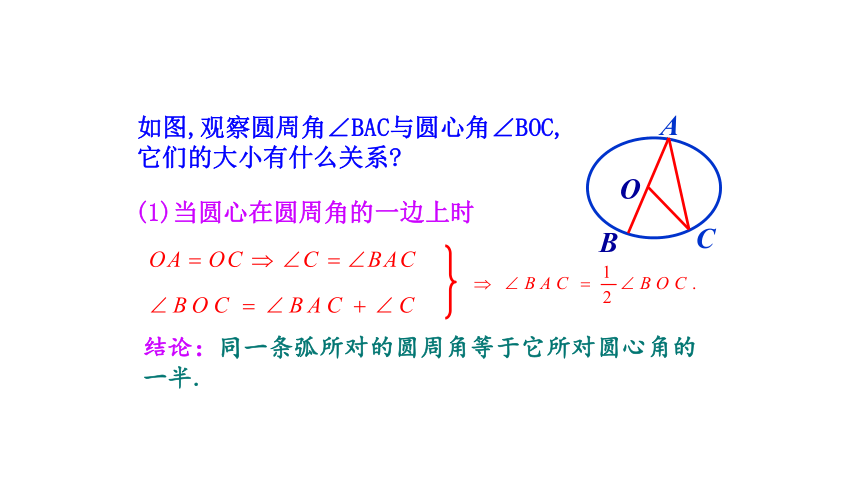
(1)当圆心在圆周角的一边上时
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
C
O
B
A
如图,观察圆周角∠BAC与圆心角∠BOC,
它们的大小有什么关系
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
(2)当圆心在圆周角外部时能否转化为(1)的情况
提示:过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC
∠ABD = ∠AOD,∠CBD = ∠COD
●
O
D
A
B
C
(3)当圆心在圆周角内部时能否转化为(1)的情况
提示:过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC.
∠ABD = ∠AOD,∠CBD = ∠COD
●O
A
B
C
D
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
【归纳】
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
也可以理解为:在同圆或等圆中,一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半.
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是⊙O上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
相等
D
A
B
O
C
E
F
问题2 如图,若 ∠A与∠B相等吗?
相等
想一想:(1)反过来,若∠A=∠B,那么 成立吗?
(2)若CD是直径,你能求出∠A的度数吗?
【推论1】
同弧或等弧所对的圆周角相等.
A1
A2
A3
O
A
B
C
2.90°的圆周角所对的弦是否是直径?
【推论2】
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
【探究】
1.半圆或直径所对的圆周角等于多少度?
如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
又在Rt△ABD中,AD2+BD2=AB2
∵AB是直径,∴∠ACB=∠ADB=90°
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
【解析】
【例题】
1.(2021 河南模拟)已知:如图,OA,OB是⊙O的两条半径,
∠AOB=100°,点C在⊙O上,则∠ACB的度数为( )
A.45° B.35° C.60° D.50°
D
【跟踪训练】
∵OA,OB是⊙O的两条半径∠AOB=100°, 由圆周角定理得,∠ACB= ∠AOB=50°.
【解析】
2.(2021 永吉县模拟)如图,点C在以AB为直径的⊙O上,BC=5,∠A=30°,则AC的长为( )
A.10 B.8 C. D.
∵AB是⊙ O的直径,∴∠ACB=90° ∵∠A=30°,∴BC= AB ∵ BC=5 ,∴ AB=10
由勾股定理得:
【解析】
D
C
O
D
B
A
定义:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做多边形的外接圆.
如图,四边形ABCD是圆O的内接四边形,圆O是四边形ABCD的外接圆.
C
O
D
B
A
【探究】如图,圆内接四边形ABCD中,
∵ ∠A的度数等于弧BCD的一半,∠BCD的度数等于弧BAD的一半,
又∵弧BCD与弧BAD的度数和为360°
∴∠A+∠C=
180°.
同理∠B+∠D=180°.
圆内接四边形的性质:圆内接四边形的对角互补.
【跟踪训练】
(2021 金台区一模)如图,四边形ABDE是⊙O的内接四边
形,CE是⊙O的直径,连接BC,DC.若∠BDC=20°,则∠A的
度数为( )
A.90° B.100° C.110° D.120°
∵CE是⊙O的直径,∴∠CDE=90° ∵∠BDC=20°,∴∠BDE=∠CDE-∠BDC=70° ∵四边形ABDE是⊙O的内接四边形, ∴∠A=180°-∠BDE=110°
【解析】
C
通过本课时的学习,需要我们掌握:
1.圆周角定义及其两个特征;
2.圆周角定理的内容及其推论;
3.圆内接多边形的有关定义;
4.圆内接四边形的性质.
1.(2021 徐州模拟)如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
A.54° B.36° C.28° D.18°
B
∵∠AOB与∠ACB都对弧AB,∠AOB=72° ∴∠ACB= ∠AOB=36°
【解析】
2.(2021 新华区模拟)如图,AB为⊙O的直径,C为半圆的中点,D为⊙O上的一点,且C、D两点分别在AB的异侧,则∠D的度数为( )
A.30° B.45° C.60° D.75°
【解析】
连接BD,如图所示: ∵AB为⊙O的直径,∴∠ADB=90° ∵C为半圆的中点, ∴∠ADC=∠BDC= ∠ADB=45°
B
3.(2021 鹿城区一模)如图,四边形ABCD是⊙O的内接四边形,它的一个外角∠CBE=70°,则∠AOC的度数为( )
A.70° B.110° C.140° D.160°
∵∠CBE是圆内接四边形ABCD的一个外角,∠CBE=70° ∴∠D=∠CBE=70° 由圆周角定理得,∠AOC=2∠D=140°
【解析】
C
数学——科学不可动摇的基石,促进人类事业进步的丰富源泉.
——巴罗
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
问题1 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图,∠BAC的顶点和边有哪些特点
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
1.理解圆周角的概念,掌握圆周角的定理的内容及简单应用.
2.掌握圆周角的定理的推论及简单应用.
3.了解圆内接多边形的有关概念.
4.掌握圆内接四边形的性质并灵活应用.
.
O
B
C
A
圆周角特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
·
C
O
A
B
·
C
O
B
A
·
C
O
B
·
C
O
B
A
A
判一判:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
O
·
C
A
B
B
C
A
·
O
(4)
● O
A
B
C
● O
A
B
C
●O
A
B
C
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系
有没有圆周角?
有没有圆心角?
它们有什么共同的特点?
它们都对着同一条弧
⌒
⌒
(1)当圆心在圆周角的一边上时
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
C
O
B
A
如图,观察圆周角∠BAC与圆心角∠BOC,
它们的大小有什么关系
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
(2)当圆心在圆周角外部时能否转化为(1)的情况
提示:过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC
∠ABD = ∠AOD,∠CBD = ∠COD
●
O
D
A
B
C
(3)当圆心在圆周角内部时能否转化为(1)的情况
提示:过点B作直径BD.由(1)可得:
∴ ∠ABC = ∠AOC.
∠ABD = ∠AOD,∠CBD = ∠COD
●O
A
B
C
D
结论:同一条弧所对的圆周角等于它所对圆心角的一半.
【归纳】
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
也可以理解为:在同圆或等圆中,一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半.
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是⊙O上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
相等
D
A
B
O
C
E
F
问题2 如图,若 ∠A与∠B相等吗?
相等
想一想:(1)反过来,若∠A=∠B,那么 成立吗?
(2)若CD是直径,你能求出∠A的度数吗?
【推论1】
同弧或等弧所对的圆周角相等.
A1
A2
A3
O
A
B
C
2.90°的圆周角所对的弦是否是直径?
【推论2】
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
【探究】
1.半圆或直径所对的圆周角等于多少度?
如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
又在Rt△ABD中,AD2+BD2=AB2
∵AB是直径,∴∠ACB=∠ADB=90°
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
【解析】
【例题】
1.(2021 河南模拟)已知:如图,OA,OB是⊙O的两条半径,
∠AOB=100°,点C在⊙O上,则∠ACB的度数为( )
A.45° B.35° C.60° D.50°
D
【跟踪训练】
∵OA,OB是⊙O的两条半径∠AOB=100°, 由圆周角定理得,∠ACB= ∠AOB=50°.
【解析】
2.(2021 永吉县模拟)如图,点C在以AB为直径的⊙O上,BC=5,∠A=30°,则AC的长为( )
A.10 B.8 C. D.
∵AB是⊙ O的直径,∴∠ACB=90° ∵∠A=30°,∴BC= AB ∵ BC=5 ,∴ AB=10
由勾股定理得:
【解析】
D
C
O
D
B
A
定义:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做多边形的外接圆.
如图,四边形ABCD是圆O的内接四边形,圆O是四边形ABCD的外接圆.
C
O
D
B
A
【探究】如图,圆内接四边形ABCD中,
∵ ∠A的度数等于弧BCD的一半,∠BCD的度数等于弧BAD的一半,
又∵弧BCD与弧BAD的度数和为360°
∴∠A+∠C=
180°.
同理∠B+∠D=180°.
圆内接四边形的性质:圆内接四边形的对角互补.
【跟踪训练】
(2021 金台区一模)如图,四边形ABDE是⊙O的内接四边
形,CE是⊙O的直径,连接BC,DC.若∠BDC=20°,则∠A的
度数为( )
A.90° B.100° C.110° D.120°
∵CE是⊙O的直径,∴∠CDE=90° ∵∠BDC=20°,∴∠BDE=∠CDE-∠BDC=70° ∵四边形ABDE是⊙O的内接四边形, ∴∠A=180°-∠BDE=110°
【解析】
C
通过本课时的学习,需要我们掌握:
1.圆周角定义及其两个特征;
2.圆周角定理的内容及其推论;
3.圆内接多边形的有关定义;
4.圆内接四边形的性质.
1.(2021 徐州模拟)如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
A.54° B.36° C.28° D.18°
B
∵∠AOB与∠ACB都对弧AB,∠AOB=72° ∴∠ACB= ∠AOB=36°
【解析】
2.(2021 新华区模拟)如图,AB为⊙O的直径,C为半圆的中点,D为⊙O上的一点,且C、D两点分别在AB的异侧,则∠D的度数为( )
A.30° B.45° C.60° D.75°
【解析】
连接BD,如图所示: ∵AB为⊙O的直径,∴∠ADB=90° ∵C为半圆的中点, ∴∠ADC=∠BDC= ∠ADB=45°
B
3.(2021 鹿城区一模)如图,四边形ABCD是⊙O的内接四边形,它的一个外角∠CBE=70°,则∠AOC的度数为( )
A.70° B.110° C.140° D.160°
∵∠CBE是圆内接四边形ABCD的一个外角,∠CBE=70° ∴∠D=∠CBE=70° 由圆周角定理得,∠AOC=2∠D=140°
【解析】
C
数学——科学不可动摇的基石,促进人类事业进步的丰富源泉.
——巴罗
同课章节目录
