24.2.1 点和圆的位置关系 课件(共25张PPT) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 24.2.1 点和圆的位置关系 课件(共25张PPT) 2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 868.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 20:39:35 | ||
图片预览





文档简介
(共25张PPT)
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
第二十四章 圆
爱好运动的小华、小强、小兵三人相邀举行一次掷飞镖比赛.他们把靶子钉在一面土墙上,规则是谁掷出的飞镖落点离红心越近,谁就胜.如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩最好?
A
B
C
1.掌握点与圆的三种位置关系的判定方法.
2.理解不在同一直线上的三个点确定一个圆.
3.理解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
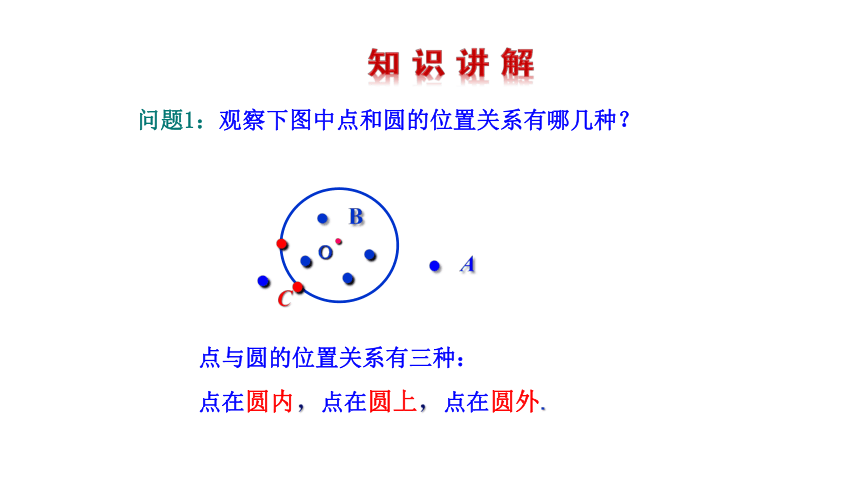
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
.B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
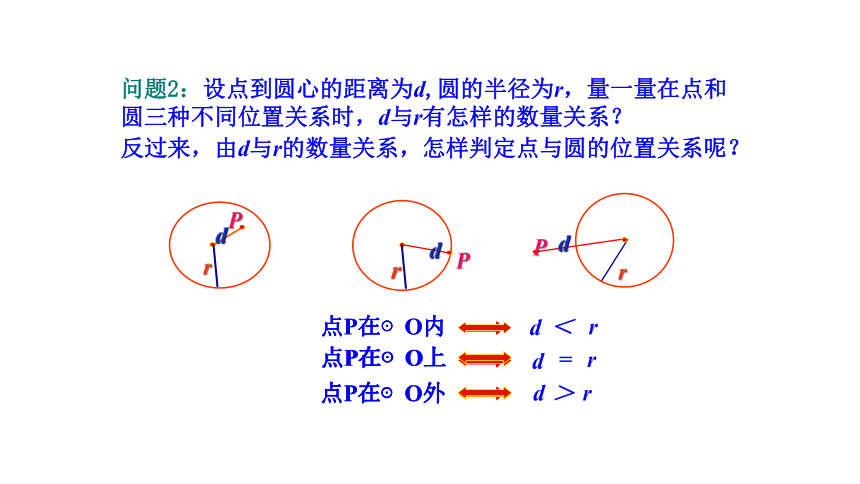
问题2:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
点P在⊙O内
点P在⊙O上
点P在⊙O外
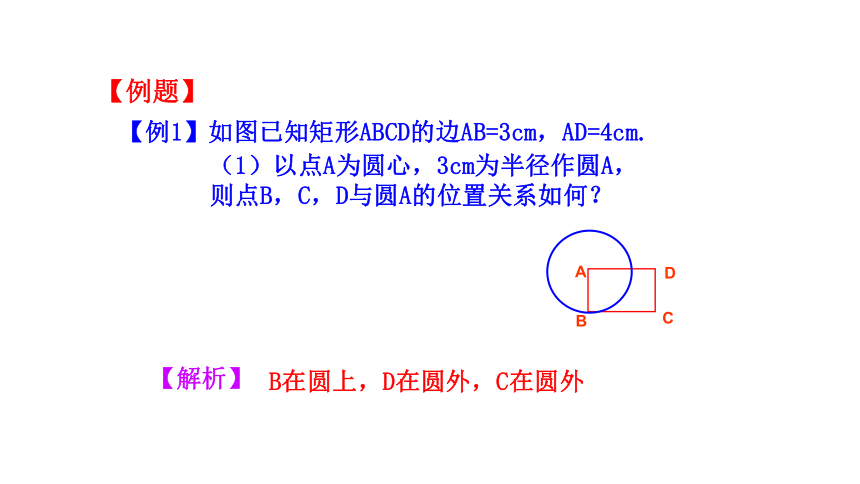
【例1】如图已知矩形ABCD的边AB=3cm,AD=4cm.
A
D
C
B
(1)以点A为圆心,3cm为半径作圆A,则点B,C,D与圆A的位置关系如何?
B在圆上,D在圆外,C在圆外
【解析】
【例题】
(2)以点A为圆心,4cm为半径作圆A,则点B,C,D与圆A的位置关系如何?
A
D
C
B
B在圆内,D在圆上,C在圆外
【解析】
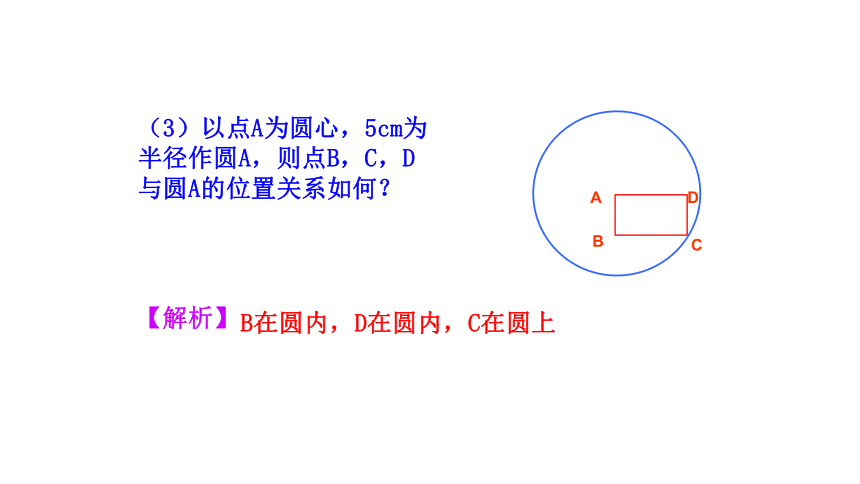
(3)以点A为圆心,5cm为
半径作圆A,则点B,C,D
与圆A的位置关系如何?
B在圆内,D在圆内,C在圆上
A
D
C
B
【解析】
1.⊙O的半径10cm,A,B,C三点到圆心的距离分别
为8cm、10cm、12cm,则点A,B,C与⊙O的位置关系
是:点A在_______;点B在______;点C在_______.
2.⊙O的半径6cm,当OP=6时,点P在________;
当OP___________时,点P在圆内;
当OP___________时,点P不在圆外.
圆内
圆上
圆外
圆上
<6
≤6
【跟踪训练】
3.正方形ABCD的边长为2cm,以A为圆心,2cm为半径作
⊙A,则点B在⊙A_____;点C在⊙A____ ;点D在⊙A_____.
外
上
上
2cm
D
c
A
B
1.平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●o
●A
●o
●o
●o
●o
【解析】无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
【探究】
2.平面上有两点A,B,经过已知点A,B的圆有几个?它们的圆心分布有什么特点?
●O
● O
●O
●O
A
B
【探究】
【解析】无数个.它们的圆心都在线段AB的垂直平分线上,以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
3.平面上有三点A,B,C,经过A,B,C三点的圆有几个?圆心在哪里?
┓
●
● C
经过B,C两点的圆的圆心在线段
BC的垂直平分线上.
┏
●O
【解析】经过A,B两点的圆的圆
心在线段AB的垂直平分线上.
●
【探究】
A
B
┓
●
● C
┏
●O
●
【归纳】
A
B
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
即:不在同一条直线上的三个点确定一个圆.
经过三角形的三个顶点可以作一个圆,并且只能画一个.
经过三角形三个顶点的圆叫作三角形的外接圆.
这个三角形叫做这个圆的内接三角形.
三角形外接圆的圆心叫做这个三角形的外心.
●O
A
B
C
有关概念
三角形的外心就是三角形三条边的垂直平分线的交点,所以外心到三角形三个顶点的距离相等.
1.一个三角形的外接圆有几个?
2.一个圆的内接三角形有几个?
3.三角形的外心有什么特征?
【想一想】
一个三角形只有一个外接圆.
一个圆的内接三角形有无数个.
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
做一做
A
B
C
O
【思考】
经过同一条直线上的三个点能作出一个圆吗?
结论:过同一条直线上的三个点不可以画圆.
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
什么叫反证法?
1.点与圆的三种位置关系.
2.不在同一条直线上的三个点确定一个圆.
3.概念:外接圆、外心.
4.反证法.
1.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆. ( )
(2)任意一个圆有且只有一个内接三角形. ( )
(3)三角形的外心到三角形各顶点的距离相等. ( )
√
×
√
1.判断:
(1)经过三点一定可以作圆 ( )
(2)三角形的外心就是这个三角形两边垂直平分线的交点 ( )
(3)三角形的外心到三边的距离相等 ( )
(4)等腰三角形的外心一定在这个三角形内 ( )
√
×
×
×
2.若一个三角形的外心在其中一边上,则此三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
【解析】
3.(2021 泗洪县二模)如图,AD为△ABC的外接圆⊙O的直径,若∠BAD=58°,则∠ACB等于( )
A.32° B.36° C.48° D.52°
连接BD ∵AD为△ABC的外接圆⊙O的直径,∠ABD=90° ∵∠BAD=58°,∴∠ADB=90°-58°=32° 由圆周角定理得,∠ACB=∠ADB=32°
A
数学家实际上是一个着迷者,不迷就没有数学.
——诺瓦利斯
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
第二十四章 圆
爱好运动的小华、小强、小兵三人相邀举行一次掷飞镖比赛.他们把靶子钉在一面土墙上,规则是谁掷出的飞镖落点离红心越近,谁就胜.如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩最好?
A
B
C
1.掌握点与圆的三种位置关系的判定方法.
2.理解不在同一直线上的三个点确定一个圆.
3.理解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
.B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
问题2:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
点P在⊙O内
点P在⊙O上
点P在⊙O外
【例1】如图已知矩形ABCD的边AB=3cm,AD=4cm.
A
D
C
B
(1)以点A为圆心,3cm为半径作圆A,则点B,C,D与圆A的位置关系如何?
B在圆上,D在圆外,C在圆外
【解析】
【例题】
(2)以点A为圆心,4cm为半径作圆A,则点B,C,D与圆A的位置关系如何?
A
D
C
B
B在圆内,D在圆上,C在圆外
【解析】
(3)以点A为圆心,5cm为
半径作圆A,则点B,C,D
与圆A的位置关系如何?
B在圆内,D在圆内,C在圆上
A
D
C
B
【解析】
1.⊙O的半径10cm,A,B,C三点到圆心的距离分别
为8cm、10cm、12cm,则点A,B,C与⊙O的位置关系
是:点A在_______;点B在______;点C在_______.
2.⊙O的半径6cm,当OP=6时,点P在________;
当OP___________时,点P在圆内;
当OP___________时,点P不在圆外.
圆内
圆上
圆外
圆上
<6
≤6
【跟踪训练】
3.正方形ABCD的边长为2cm,以A为圆心,2cm为半径作
⊙A,则点B在⊙A_____;点C在⊙A____ ;点D在⊙A_____.
外
上
上
2cm
D
c
A
B
1.平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●o
●A
●o
●o
●o
●o
【解析】无数个,圆心为点A以外任意一点,半径为这点与点A的距离.
【探究】
2.平面上有两点A,B,经过已知点A,B的圆有几个?它们的圆心分布有什么特点?
●O
● O
●O
●O
A
B
【探究】
【解析】无数个.它们的圆心都在线段AB的垂直平分线上,以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
3.平面上有三点A,B,C,经过A,B,C三点的圆有几个?圆心在哪里?
┓
●
● C
经过B,C两点的圆的圆心在线段
BC的垂直平分线上.
┏
●O
【解析】经过A,B两点的圆的圆
心在线段AB的垂直平分线上.
●
【探究】
A
B
┓
●
● C
┏
●O
●
【归纳】
A
B
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
即:不在同一条直线上的三个点确定一个圆.
经过三角形的三个顶点可以作一个圆,并且只能画一个.
经过三角形三个顶点的圆叫作三角形的外接圆.
这个三角形叫做这个圆的内接三角形.
三角形外接圆的圆心叫做这个三角形的外心.
●O
A
B
C
有关概念
三角形的外心就是三角形三条边的垂直平分线的交点,所以外心到三角形三个顶点的距离相等.
1.一个三角形的外接圆有几个?
2.一个圆的内接三角形有几个?
3.三角形的外心有什么特征?
【想一想】
一个三角形只有一个外接圆.
一个圆的内接三角形有无数个.
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
做一做
A
B
C
O
【思考】
经过同一条直线上的三个点能作出一个圆吗?
结论:过同一条直线上的三个点不可以画圆.
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
什么叫反证法?
1.点与圆的三种位置关系.
2.不在同一条直线上的三个点确定一个圆.
3.概念:外接圆、外心.
4.反证法.
1.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆. ( )
(2)任意一个圆有且只有一个内接三角形. ( )
(3)三角形的外心到三角形各顶点的距离相等. ( )
√
×
√
1.判断:
(1)经过三点一定可以作圆 ( )
(2)三角形的外心就是这个三角形两边垂直平分线的交点 ( )
(3)三角形的外心到三边的距离相等 ( )
(4)等腰三角形的外心一定在这个三角形内 ( )
√
×
×
×
2.若一个三角形的外心在其中一边上,则此三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
【解析】
3.(2021 泗洪县二模)如图,AD为△ABC的外接圆⊙O的直径,若∠BAD=58°,则∠ACB等于( )
A.32° B.36° C.48° D.52°
连接BD ∵AD为△ABC的外接圆⊙O的直径,∠ABD=90° ∵∠BAD=58°,∴∠ADB=90°-58°=32° 由圆周角定理得,∠ACB=∠ADB=32°
A
数学家实际上是一个着迷者,不迷就没有数学.
——诺瓦利斯
同课章节目录
