24.2.2 直线和圆的位置关系 第2课时 课件(共22张PPT) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 第2课时 课件(共22张PPT) 2024-2025学年人教版数学九年级上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 667.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 20:42:23 | ||
图片预览








文档简介
(共22张PPT)
24.2.2 直线和圆的位置关系
第2课时
第二十四章 圆
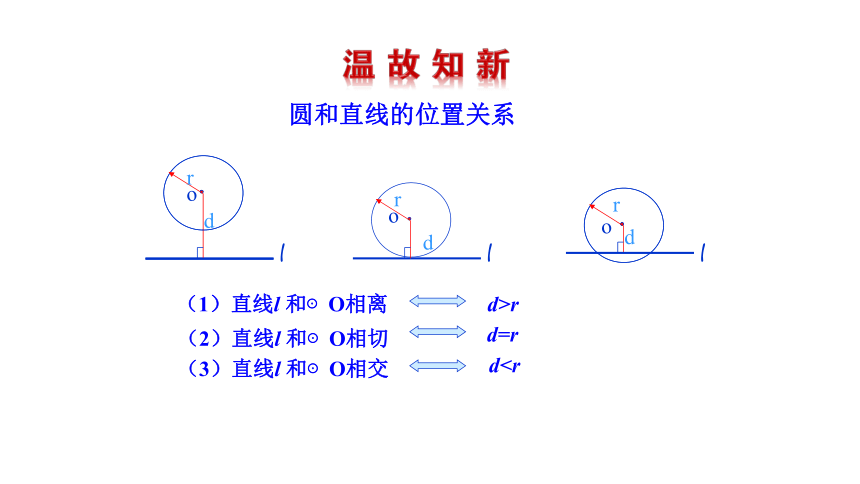
(2)直线l 和⊙O相切
(3)直线l 和⊙O相交
d>r
d=r
dd
o
r
l
d
o
r
l
o
d
r
l
(1)直线l 和⊙O相离
圆和直线的位置关系
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的
位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
3.判断:
若直线和圆相切,则该直线和圆一定有一个公共点.( )
A
C
√
1.会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.
2.理解并掌握圆的切线的判定定理及性质定理.(重点)
3.能运用圆的切线的判定定理和性质定理解决问题.(难点)
O
l
A
【探究】请在⊙O上任意取一点A,连接OA,过点A作直线 l⊥OA.思考一下问题:
1.圆心O到直线l的距离和圆的半径有什么数量关系
2.二者位置有什么关系?为什么?
3.由此你发现了什么?
(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从几何角度上来判定直线是圆的切线的方法——切线的判定定理.
A
O
l
【发现】
切线需满足的两条:①经过半径外端;
②垂直于这条半径.
【归纳】
切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线.
O
r
l
A
∵ OA是半径
l ⊥ OA于点A
∴ l是⊙O的切线
定理的几何符号表达:
判一判:下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
注意
例1 如图,∠ABC=45°,AB是☉O的直径,直线AC经过点A,且AB=AC.
求证:AC是☉O的切线.
解析:直线AC经过半径的一端,因此只要证OA垂直于AC即可.
证明:∵AB=AC,∠ABC=45°
∴∠ACB=∠ABC=45°
∴∠BAC=180°-∠ABC-ACB=90°
∵AB是☉O的直径
∴ AC是☉O的切线
A
O
C
B
【例题】
例2 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可.
证明:连接OC(如图)
∵ OA=OB,CA=CB
∴ OC是等腰三角形OAB底边AB上的中线
∴ AB⊥OC
∵ OC是⊙O的半径
∴ AB是⊙O的切线
1.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
【跟踪训练】
∵OD⊥a于D, ∴以点O为圆心,OD为半径的圆与直线a相切.
【解析】
D
2.(2021 崆峒区一模)如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC.求证:DE是⊙O的切线.
∵D是BC的中点 ∴BD=CD ∵OA=OB ∴OD∥AC 又∵DE⊥AC ∴OD⊥DE ∴DE是⊙O的切线
证明:
连接OD
当已知直线与圆有公共点,要证明直线与圆相切时,可先连接圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.
【归纳】
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
【归纳】
.
O
A
l
如果l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径.
【探究】
1.切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线.
2.切线的性质定理:圆的切线垂直于过切点的半径.
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
例1
例2
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
1.(2021 苏州模拟)如图,AB是⊙O的直径,PA切于点A,线段PO交⊙O于点C,连接BC.若∠P=40°,则∠B等于( )
A.15° B.20° C.25° D.30°
【解析】
∵AB是⊙O的直径,PA切于点A ∴∠OAP=90° 又∵∠P=40° ∴∠AOP=90°-40°=50° 又∵OA=OC ∴∠B=∠OCB= ∠AOP=25°
C
【解析】
2.(2021 黄梅县模拟)如图,AB是⊙O的直径,C是弧AB的中点,延长AC至D,使CD=AC,连接DB.E是OB的中点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.求证:BD是⊙O的切线;
连接OC,先由垂径定理可知OC⊥AB, 再证明OC为△ABD的中位线,得到OC∥BD,由平行线的性质可得BD⊥AB,然后由切线的判定定理可得结论;
如图,连接OC ∵AB是⊙O的直径,C是弧AB的中点 ∴OC⊥AB ∵CD=AC,OA=OB ∴OC为△ABD的中位线 ∴OC∥BD ∴BD⊥AB ∴BD是⊙O的切线
证明:
一个人的贡献和他的自负严格地成反比,这似乎是品行上的一个公理.
——拉格朗日
24.2.2 直线和圆的位置关系
第2课时
第二十四章 圆
(2)直线l 和⊙O相切
(3)直线l 和⊙O相交
d>r
d=r
d
o
r
l
d
o
r
l
o
d
r
l
(1)直线l 和⊙O相离
圆和直线的位置关系
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的
位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
3.判断:
若直线和圆相切,则该直线和圆一定有一个公共点.( )
A
C
√
1.会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.
2.理解并掌握圆的切线的判定定理及性质定理.(重点)
3.能运用圆的切线的判定定理和性质定理解决问题.(难点)
O
l
A
【探究】请在⊙O上任意取一点A,连接OA,过点A作直线 l⊥OA.思考一下问题:
1.圆心O到直线l的距离和圆的半径有什么数量关系
2.二者位置有什么关系?为什么?
3.由此你发现了什么?
(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从几何角度上来判定直线是圆的切线的方法——切线的判定定理.
A
O
l
【发现】
切线需满足的两条:①经过半径外端;
②垂直于这条半径.
【归纳】
切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线.
O
r
l
A
∵ OA是半径
l ⊥ OA于点A
∴ l是⊙O的切线
定理的几何符号表达:
判一判:下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
注意
例1 如图,∠ABC=45°,AB是☉O的直径,直线AC经过点A,且AB=AC.
求证:AC是☉O的切线.
解析:直线AC经过半径的一端,因此只要证OA垂直于AC即可.
证明:∵AB=AC,∠ABC=45°
∴∠ACB=∠ABC=45°
∴∠BAC=180°-∠ABC-ACB=90°
∵AB是☉O的直径
∴ AC是☉O的切线
A
O
C
B
【例题】
例2 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可.
证明:连接OC(如图)
∵ OA=OB,CA=CB
∴ OC是等腰三角形OAB底边AB上的中线
∴ AB⊥OC
∵ OC是⊙O的半径
∴ AB是⊙O的切线
1.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
【跟踪训练】
∵OD⊥a于D, ∴以点O为圆心,OD为半径的圆与直线a相切.
【解析】
D
2.(2021 崆峒区一模)如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC.求证:DE是⊙O的切线.
∵D是BC的中点 ∴BD=CD ∵OA=OB ∴OD∥AC 又∵DE⊥AC ∴OD⊥DE ∴DE是⊙O的切线
证明:
连接OD
当已知直线与圆有公共点,要证明直线与圆相切时,可先连接圆心与公共点,再证明连线垂直于直线 ,这是证明切线的一种方法.
【归纳】
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
【归纳】
.
O
A
l
如果l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径.
【探究】
1.切线的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线.
2.切线的性质定理:圆的切线垂直于过切点的半径.
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
例1
例2
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
1.(2021 苏州模拟)如图,AB是⊙O的直径,PA切于点A,线段PO交⊙O于点C,连接BC.若∠P=40°,则∠B等于( )
A.15° B.20° C.25° D.30°
【解析】
∵AB是⊙O的直径,PA切于点A ∴∠OAP=90° 又∵∠P=40° ∴∠AOP=90°-40°=50° 又∵OA=OC ∴∠B=∠OCB= ∠AOP=25°
C
【解析】
2.(2021 黄梅县模拟)如图,AB是⊙O的直径,C是弧AB的中点,延长AC至D,使CD=AC,连接DB.E是OB的中点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.求证:BD是⊙O的切线;
连接OC,先由垂径定理可知OC⊥AB, 再证明OC为△ABD的中位线,得到OC∥BD,由平行线的性质可得BD⊥AB,然后由切线的判定定理可得结论;
如图,连接OC ∵AB是⊙O的直径,C是弧AB的中点 ∴OC⊥AB ∵CD=AC,OA=OB ∴OC为△ABD的中位线 ∴OC∥BD ∴BD⊥AB ∴BD是⊙O的切线
证明:
一个人的贡献和他的自负严格地成反比,这似乎是品行上的一个公理.
——拉格朗日
同课章节目录
