25.3 用频率估计概率 课件(共18张PPT)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 25.3 用频率估计概率 课件(共18张PPT)2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 846.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第二十五章 概率初步
25.3 用频率估计概率
1.什么叫概率?
一般地,对于一个随机事件A,我们把刻画其可能性大小的数值,称为随机事件A发生的概率,记为P(A).
2.概率的计算公式:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率
理解每次试验可能结果不是有限个,或各种可能结果发生的可能性不相等时,用频率估计概率的方法.
2.能应用模拟实验求概率及其应用.
1.如果有人买了彩票,一定希望知道中奖的概率有多大.那么怎样来估计中奖的概率呢?
2.出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小?
概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
数学史实
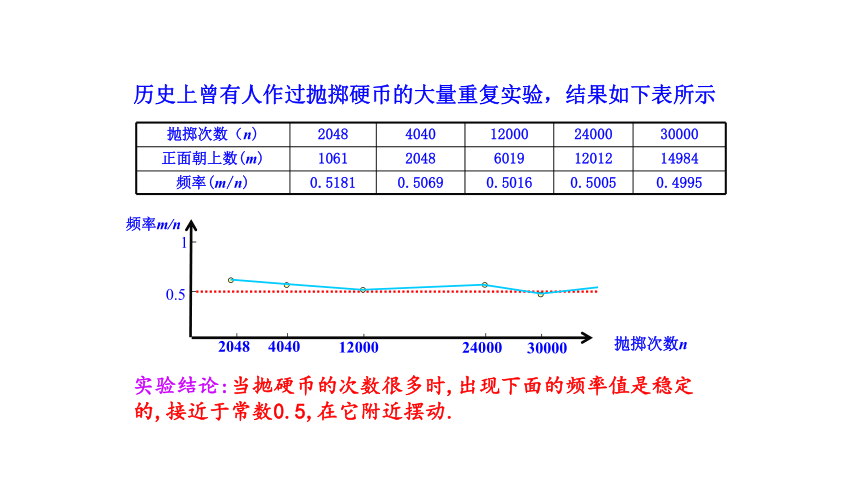
抛掷次数(n) 2048 4040 12000 24000 30000
正面朝上数(m) 1061 2048 6019 12012 14984
频率(m/n) 0.5181 0.5069 0.5016 0.5005 0.4995
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
实验结论:当抛硬币的次数很多时,出现下面的频率值是稳定的,接近于常数0.5,在它附近摆动.
某批乒乓球产品质量检查结果表:
当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动.
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数
抽取球数
当试验的油菜籽的粒数很多时,油菜籽发芽的频率 接近于常数0.9,在它附近摆动.
某种油菜籽在相同条件下的发芽试验结果表:
对一般的随机事件在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性,因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
【归纳】
对一批衬衫进行抽查,结果如下表:
抽取件数n 50 100 200 500 800 1000
优等品件数m 42 88 176 445 724 901
优等品频率m/n 0.84 0.88
0.88
0.89
0.901
0.905
求抽取一件衬衫是优等品的概率约是多少?(结果保留0.1),抽取衬衫2000件,约有优质品几件?
【例题】
【解析】抽取一件衬衫是优等品的概率约是0.9,抽取衬衫2000件,约有优质品2000×0.9=1800(件).
某篮球队教练记录该队一名主力前锋练习罚篮的结果如下:
(1)填表(精确到0.001);
(2)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,
你能估计这次他能罚中的概率是多少吗?
练习罚篮次数 30 60 90 150 200 300 400 500
罚中次数 27 45 78 118 161 239 322 401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
解:从表中的数据可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
【跟踪训练】
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
1.用频率估计概率的条件及方法,应用以上的内容解决一些实际问题.
2.从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,可以发现:在大量的偶然之中存在着必然的规律.
A
1.(2021 石家庄模拟)某射击运动员在同一条件下的射击成绩记录如下:
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.82 B.0.84 C.0.85 D.0.90
2.(2021 泰兴)在一个不透明的布袋中装有45个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.4左右,则布袋中黑球的个数可能有( )
A.18 B.27 C.36 D.30
【解析】设袋子中黑球的个数为x,根据题意,得:
x/(45+x)=0.4, 解得x=30 经检验x=30是分式方程的解, 所以袋子中黑球的个数为30, 故选:D
D
3. (2021 海门市模拟)在一个不透明的盒子中装有a个黑白颜色的球,小明又放入了5个红球,这些球大小相同.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值大约为( )
A.15 B.20 C.25 D.30
B
【解析】由题意可得,5/(5+a)×100%=20%, 解得,a=20 经检验:a=20是原分式方程的解, 所以a=20 故选:B
如果我们想要预见数学的将来, 适当的途径是研究这门学科的历史和现状。
——庞加莱
第二十五章 概率初步
25.3 用频率估计概率
1.什么叫概率?
一般地,对于一个随机事件A,我们把刻画其可能性大小的数值,称为随机事件A发生的概率,记为P(A).
2.概率的计算公式:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率
理解每次试验可能结果不是有限个,或各种可能结果发生的可能性不相等时,用频率估计概率的方法.
2.能应用模拟实验求概率及其应用.
1.如果有人买了彩票,一定希望知道中奖的概率有多大.那么怎样来估计中奖的概率呢?
2.出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小?
概率与人们生活密切相关,在生活,生产和科研等各个领域都有着广泛的应用.
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
数学史实
抛掷次数(n) 2048 4040 12000 24000 30000
正面朝上数(m) 1061 2048 6019 12012 14984
频率(m/n) 0.5181 0.5069 0.5016 0.5005 0.4995
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
实验结论:当抛硬币的次数很多时,出现下面的频率值是稳定的,接近于常数0.5,在它附近摆动.
某批乒乓球产品质量检查结果表:
当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动.
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数
抽取球数
当试验的油菜籽的粒数很多时,油菜籽发芽的频率 接近于常数0.9,在它附近摆动.
某种油菜籽在相同条件下的发芽试验结果表:
对一般的随机事件在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性,因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
【归纳】
对一批衬衫进行抽查,结果如下表:
抽取件数n 50 100 200 500 800 1000
优等品件数m 42 88 176 445 724 901
优等品频率m/n 0.84 0.88
0.88
0.89
0.901
0.905
求抽取一件衬衫是优等品的概率约是多少?(结果保留0.1),抽取衬衫2000件,约有优质品几件?
【例题】
【解析】抽取一件衬衫是优等品的概率约是0.9,抽取衬衫2000件,约有优质品2000×0.9=1800(件).
某篮球队教练记录该队一名主力前锋练习罚篮的结果如下:
(1)填表(精确到0.001);
(2)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,
你能估计这次他能罚中的概率是多少吗?
练习罚篮次数 30 60 90 150 200 300 400 500
罚中次数 27 45 78 118 161 239 322 401
罚中频率
0.900
0.750
0.867
0.787
0.805
0.797
0.805
0.802
解:从表中的数据可以发现,随着练习次数的增加,该前锋罚篮命中的频率稳定在0.8左右,所以估计他这次能罚中的概率约为0.8.
【跟踪训练】
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
1.用频率估计概率的条件及方法,应用以上的内容解决一些实际问题.
2.从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,可以发现:在大量的偶然之中存在着必然的规律.
A
1.(2021 石家庄模拟)某射击运动员在同一条件下的射击成绩记录如下:
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.82 B.0.84 C.0.85 D.0.90
2.(2021 泰兴)在一个不透明的布袋中装有45个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.4左右,则布袋中黑球的个数可能有( )
A.18 B.27 C.36 D.30
【解析】设袋子中黑球的个数为x,根据题意,得:
x/(45+x)=0.4, 解得x=30 经检验x=30是分式方程的解, 所以袋子中黑球的个数为30, 故选:D
D
3. (2021 海门市模拟)在一个不透明的盒子中装有a个黑白颜色的球,小明又放入了5个红球,这些球大小相同.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值大约为( )
A.15 B.20 C.25 D.30
B
【解析】由题意可得,5/(5+a)×100%=20%, 解得,a=20 经检验:a=20是原分式方程的解, 所以a=20 故选:B
如果我们想要预见数学的将来, 适当的途径是研究这门学科的历史和现状。
——庞加莱
同课章节目录
