2.2.4二次函数的图象与性质 课件(共19张PPT) 北师大版数学九年级下册
文档属性
| 名称 | 2.2.4二次函数的图象与性质 课件(共19张PPT) 北师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1023.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
课前听写
1. (1)抛物线y=x2向右平移1个单位长度,得到的抛物线表达式为 __________ ;向下平移2个单位长度,得到的抛物线表达式为 .
(2)猜想:抛物线y=x2先向右平移1个单位长度,再向下平移2个单位长度,得到的抛物线表达式为 .
y=(x-1)2
y=x2-2
y=(x-1)2-2
1
18
2. 画出二次函数y=(x-1)2-2草图,并描述性质。
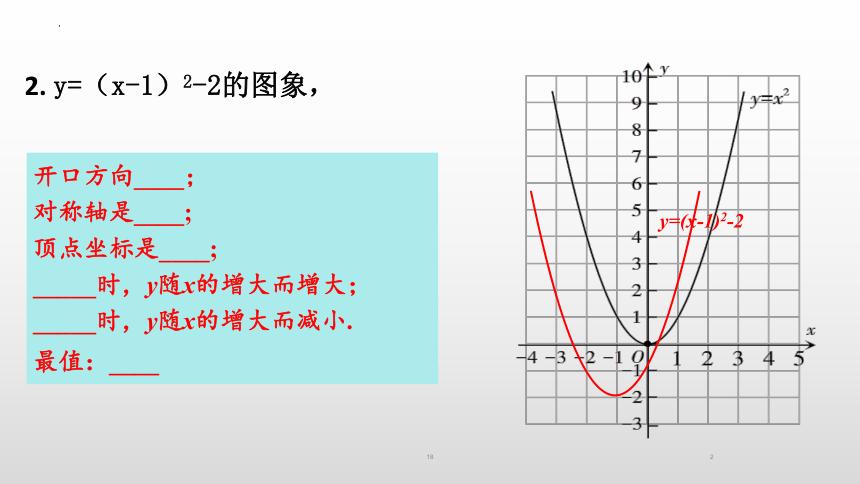
2. y=(x-1)2-2的图象,
y=(x-1)2-2
开口方向____;
对称轴是____;
顶点坐标是____;
_____时,y随x的增大而增大;
_____时,y随x的增大而减小.
最值:____
2
18
第二章
二次函数
二次函数
表达式
二次函数与
一元二次方程
图象与性质
应用
2.2.二次函数的图象与性质(四)
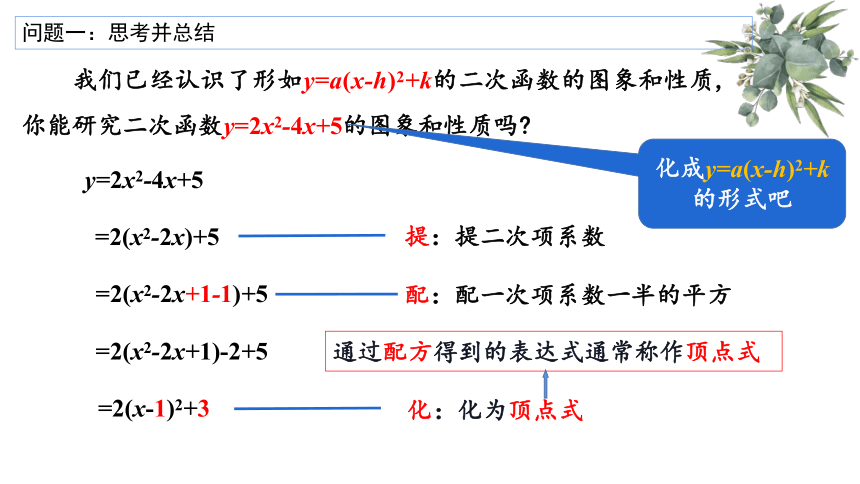
问题一:思考并总结
我们已经认识了形如y=a(x-h)2+k的二次函数的图象和性质, 你能研究二次函数y=2x2-4x+5的图象和性质吗
化成y=a(x-h)2+k的形式吧
y=2x2-4x+5
=2(x2-2x)+5
=2(x2-2x+1-1)+5
=2(x2-2x+1)-2+5
=2(x-1)2+3
提:提二次项系数
配:配一次项系数一半的平方
通过配方得到的表达式通常称作顶点式
化:化为顶点式
任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
例1.求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
解: y=2x2-8x+7
y=2(x2-4x)+7
y=2(x2-4x+4)-8+7
y=2(x-2)2-1
∴二次函数y=2x2-8x+7图象的对称轴是直线x=2,
顶点坐标为(2,-1).
评价任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
1.确定下列二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
(1) y=3x2-6x+7; (2) y=2x2-12x+8;
解:对称轴: 直线x=1 直线x=3 直线x=-6
顶点坐标: (1,4) (3,-10) (-6,27)
任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
例2.求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
解:
∴二次函数y=ax2+bx+c图象的对称轴是直线 ,顶点坐标为 .
知识点二:用公式法求二次函数y=ax2+bx+c顶点坐标及坐标轴
评价任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
2.把二次函数 用配方法化成
的形式为( ).
A. B.
C. D.
C
评价任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
3.抛物线 的顶点在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
任务二:实际应用(指向目标二)
如图,桥梁的两条钢缆具有相同的抛物线形状,而且左右两条抛物线关于y轴对称.按照图中的直角坐标系,左面的一条抛物线可以用 表示.
(1)钢缆的最低点到桥面的距离是多少
(2)两条钢缆最低点之间的距离是多少
5
-5
O
10
x/m
y/m
桥面
解:(1)
所以左侧钢缆最低点坐标为(-20,1),
即钢缆最低点到桥面的距离是1m.
5
-5
O
10
x/m
y/m
任务二:实际应用(指向目标二)
(2)由对称性可知,两条钢缆最低点之间距离为40米.
评价任务二:实际应用(指向目标二)
4.当火箭竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式 表示.经过多长时间,火箭到达它的最高点?最高点的高度是多少?
答案:15s,1135米.
指出下列函数的开口方向、对称轴和顶点坐标
当堂检测:
评价任务二:实际应用(指向目标二)
3.有心理学家研究发现,学生对某类概念的接受能力y与讲授概念所用时间x(min)之间满足函数关系
y值越大,表示接受能力越强.根据这一结论回答下列问题.
(1)x在什么范围内,学生的接受能力逐步增强?
在什么范围内,学生的接受能力逐渐减降低?
(2)经过多长时间,学生的接受能力最强?
答案:(1)当 ,学生接受能力逐渐增强;当x=13时,学生接受能力最强;当 时,学生接受能力逐渐降低.
(2)13min
将二次函数 的图像向上平移2个单位长度,再向左平移3个单位长度,得到抛物线 ,求b,c的值,并求出这条抛物线的开后方向、对称轴和顶点坐标。
思维提升:
课堂小结
1.今天的收获是什么?
2.请你评价一下你的表现和同学们的表现。
1.用会配方法将二次函数一般式y=ax +bx+c化成顶点式y=a(x-h) +k,并求出函数图象的对称轴和顶点坐标.
2.灵活运用配方法或顶点坐标公式,通过对称性,解决实际问题.
课前听写
1. (1)抛物线y=x2向右平移1个单位长度,得到的抛物线表达式为 __________ ;向下平移2个单位长度,得到的抛物线表达式为 .
(2)猜想:抛物线y=x2先向右平移1个单位长度,再向下平移2个单位长度,得到的抛物线表达式为 .
y=(x-1)2
y=x2-2
y=(x-1)2-2
1
18
2. 画出二次函数y=(x-1)2-2草图,并描述性质。
2. y=(x-1)2-2的图象,
y=(x-1)2-2
开口方向____;
对称轴是____;
顶点坐标是____;
_____时,y随x的增大而增大;
_____时,y随x的增大而减小.
最值:____
2
18
第二章
二次函数
二次函数
表达式
二次函数与
一元二次方程
图象与性质
应用
2.2.二次函数的图象与性质(四)
问题一:思考并总结
我们已经认识了形如y=a(x-h)2+k的二次函数的图象和性质, 你能研究二次函数y=2x2-4x+5的图象和性质吗
化成y=a(x-h)2+k的形式吧
y=2x2-4x+5
=2(x2-2x)+5
=2(x2-2x+1-1)+5
=2(x2-2x+1)-2+5
=2(x-1)2+3
提:提二次项系数
配:配一次项系数一半的平方
通过配方得到的表达式通常称作顶点式
化:化为顶点式
任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
例1.求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
解: y=2x2-8x+7
y=2(x2-4x)+7
y=2(x2-4x+4)-8+7
y=2(x-2)2-1
∴二次函数y=2x2-8x+7图象的对称轴是直线x=2,
顶点坐标为(2,-1).
评价任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
1.确定下列二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
(1) y=3x2-6x+7; (2) y=2x2-12x+8;
解:对称轴: 直线x=1 直线x=3 直线x=-6
顶点坐标: (1,4) (3,-10) (-6,27)
任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
例2.求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
解:
∴二次函数y=ax2+bx+c图象的对称轴是直线 ,顶点坐标为 .
知识点二:用公式法求二次函数y=ax2+bx+c顶点坐标及坐标轴
评价任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
2.把二次函数 用配方法化成
的形式为( ).
A. B.
C. D.
C
评价任务一:配方法求二次函数图象的对称轴和顶点坐标(指向目标一)
3.抛物线 的顶点在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
任务二:实际应用(指向目标二)
如图,桥梁的两条钢缆具有相同的抛物线形状,而且左右两条抛物线关于y轴对称.按照图中的直角坐标系,左面的一条抛物线可以用 表示.
(1)钢缆的最低点到桥面的距离是多少
(2)两条钢缆最低点之间的距离是多少
5
-5
O
10
x/m
y/m
桥面
解:(1)
所以左侧钢缆最低点坐标为(-20,1),
即钢缆最低点到桥面的距离是1m.
5
-5
O
10
x/m
y/m
任务二:实际应用(指向目标二)
(2)由对称性可知,两条钢缆最低点之间距离为40米.
评价任务二:实际应用(指向目标二)
4.当火箭竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式 表示.经过多长时间,火箭到达它的最高点?最高点的高度是多少?
答案:15s,1135米.
指出下列函数的开口方向、对称轴和顶点坐标
当堂检测:
评价任务二:实际应用(指向目标二)
3.有心理学家研究发现,学生对某类概念的接受能力y与讲授概念所用时间x(min)之间满足函数关系
y值越大,表示接受能力越强.根据这一结论回答下列问题.
(1)x在什么范围内,学生的接受能力逐步增强?
在什么范围内,学生的接受能力逐渐减降低?
(2)经过多长时间,学生的接受能力最强?
答案:(1)当 ,学生接受能力逐渐增强;当x=13时,学生接受能力最强;当 时,学生接受能力逐渐降低.
(2)13min
将二次函数 的图像向上平移2个单位长度,再向左平移3个单位长度,得到抛物线 ,求b,c的值,并求出这条抛物线的开后方向、对称轴和顶点坐标。
思维提升:
课堂小结
1.今天的收获是什么?
2.请你评价一下你的表现和同学们的表现。
1.用会配方法将二次函数一般式y=ax +bx+c化成顶点式y=a(x-h) +k,并求出函数图象的对称轴和顶点坐标.
2.灵活运用配方法或顶点坐标公式,通过对称性,解决实际问题.
