【中考考点探究】第1节 平面直角坐标系与函数 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第1节 平面直角坐标系与函数 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:34:55 | ||
图片预览




文档简介
第1节 平面直角坐标系与函数
(6年3考,2~4分)
河北中考试卷中,会单独考查坐标平面内点的特征或规律,以及实际问题中函数图象的意义;也常把平面直角坐标系、函数概念与自变量取值范围、函数图象的知识,融入到一次函数、二次函数或反比例函数中,通过具体类型的函数进行考查,预计2025年对本节知识的考查,在选择题中以“独立式”为主,在解答题中以“融入式”为主.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1平面直角坐标系
相关概念1.定义:在平面内有公共原点且互相垂直的两条数轴构成平面直角坐标系. 2.几何意义:坐标平面内任意一点M与有序实数对(x,y)的关系是一一对应
点的坐标特征1.各象限内点的坐标的符号特征(如图所示): (1)点P(x,y)在第一象限 x① 0,y② 0, (2)点P(x,y)在第二象限 x③ 0,y④ 0, (3)点P(x,y)在第三象限 x⑤ 0,y⑥ 0, (4)点P(x,y)在第四象限 x⑦ 0,y⑧ 0. 【温馨提示】坐标轴上的点不属于任何象限. 2.坐标轴上点的坐标特征: (1)在横轴上 y=0. (2)在纵轴上 x=0. (3)原点 x=0,y=0
点的坐标 特征3.各象限角平分线上点的坐标: (1)第一、三象限角平分线上的点的横、纵坐标⑨ . (2)第二、四象限角平分线上的点的横、纵坐标⑩ . 4.点P(a,b)的对称点的坐标特征: (1)关于x轴对称的点P1的坐标为(a,-b). (2)关于y轴对称的点P2的坐标为(-a,b). (3)关于原点对称的点P3的坐标为(-a,-b). 5.点M(x,y)平移的坐标特征: M(x,y)M1( , )M2( , )
点的坐标 距离问题1.点M(a,b)到x轴,y轴的距离:到x轴的距离为 ;到y轴的距离为 ;到原点的距离为. 2.坐标轴上两点间的距离与平行于x轴,y轴直线上的两点间的距离: (1)点M1(x1,0),M2(x2,0)之间的距离为|x1-x2|. (2)点M1(x1,y),M2(x2,y)间的距离为|x1-x2|. (3)点M1(0,y1),M2(0,y2)间的距离为|y1-y2|. (4)点M1(x,y1),M2(x,y2)间的距离为|y1-y2|. 3.任意两点间的距离:点A(x1,y1),B(x2,y2)间的距离为
考点2函数
函数的相关概念1.常量、变量:在一个变化过程中,数值始终不变的量叫作常量,数值发生变化的量叫作变量. 2.函数:在一个变化过程中,有两个变量x和y,对于x的每一个值,y都有唯一确定的值与其对应,那么就称x是自变量,y是x的函数.函数的表示方法:列表法、图象法、解析式法. 3.函数自变量的取值范围:一般原则,整式为全体实数;分式的分母不为 ;二次根式的被开方数为 数;使实际问题有意义
函数的图象1.分析实际问题判断函数图象的方法: (1)找起点:结合题干中所给自变量及因变量的取值范围,对应到图象中找对应点. (2)找特殊点:即交点或转折点,说明图象在此点处将发生变化. (3)判断图象趋势:判断出函数的增减性,图象的倾斜方向. 2.画函数图象的步骤:列表、描点、连线
【基础演练】
1.(人教七下P84第1题变式)在平面直角坐标系中,第二象限内的点可能是 ( )
A.(1,2)
B.(1,-2)
C.(-1,2)
D.(-1,-2)
2.(人教七下P70第8题(2)变式)在平面直角坐标系中,直线AB平行于y轴,点A的坐标为(-3,2),点B的坐标可能为 ( )
A.(4,2) B.(-3,4)
C.(3,-4) D.(-4,2)
3.(冀教八下P40练习第2题变式)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 ( )
A.(-3,2) B.(-2,3)
C.(2,-3) D.(3,-2)
4.在平面直角坐标系中,点M(m-1,2m)在x轴上,则点M的坐标是 ( )
A.(1,0) B.(-1,0)
C.(0,2) D.(0,-1)
5.(冀教八下P39第1题变式)在平面直角坐标系中,点P(2,-3)到x轴的距离是 .
6.(冀教八下P67做一做第1题变式)函数y=的自变量x的取值范围是 .
7.全世界大约有19 000种蝴蝶,大部分分布在美洲,尤其在亚马孙河流域品种最多,在世界其他地区除了南北极寒冷地带以外都有分布.如图,这是一个蝴蝶标本,将其放在适当的平面直角坐标系中,若翅膀两端B,C两点的坐标分别为(-1,3),(3,0),则蝴蝶尾部点A的坐标为 .
真题精粹·重变式——河北6年真题精选及拓展
考向1平面直角坐标系 (6年2考)
1.(2024·河北12题2分)在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形ABCD位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是 ( )
A.点A B.点B
C.点C D.点D
2.(2024·河北16题2分)在平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.
例:“和点”P(2,1)按上述规则连续平移3次后,到达点P3(2,2),其平移过程如下:P1P2P3(2,2).
若“和点”Q按上述规则连续平移16次后,到达点Q16(-1,9),则点Q的坐标为 ( )
A.(6,1)或(7,1)
B.(15,-7)或(8,0)
C.(6,0)或(8,0)
D.(5,1)或(7,1)
考向2动点问题的函数图象 (6年1考)
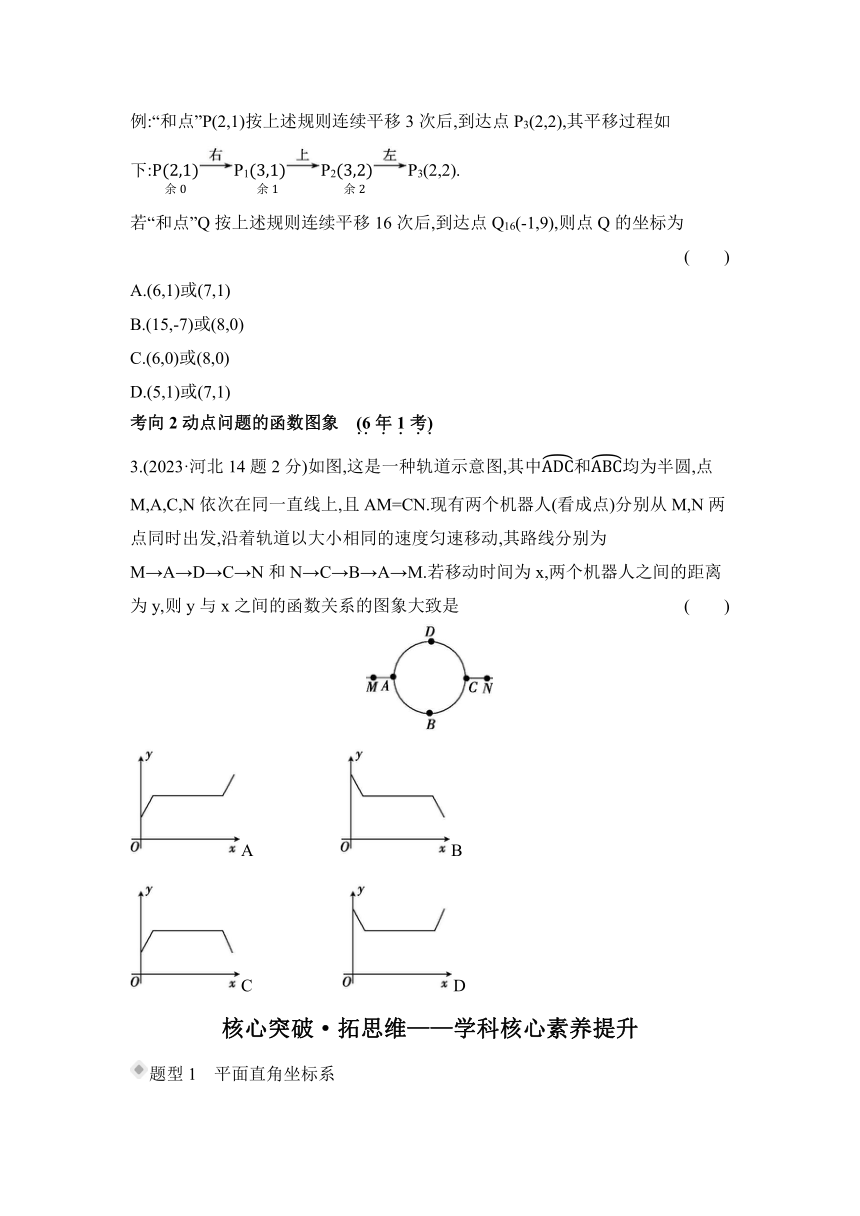
3.(2023·河北14题2分)如图,这是一种轨道示意图,其中和均为半圆,点M,A,C,N依次在同一直线上,且AM=CN.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M→A→D→C→N和N→C→B→A→M.若移动时间为x,两个机器人之间的距离为y,则y与x之间的函数关系的图象大致是 ( )
A B
C D
核心突破·拓思维——学科核心素养提升
题型1 平面直角坐标系
(原创)如图,这是某台阶的一部分,点A与点B的水平距离以及每级台阶的水平、竖直距离都等于2,地面与x轴平行,点D的坐标为(2,2).
(1)请你在图中建立适当的平面直角坐标系.
(2)直接写出点A,E,F的坐标.
(3)如果台阶有10级(第11个点用M表示),请你求出该台阶到地面的距离和线段AM的长度.
由已知点求其他点的坐标的步骤
已知点的坐标确定原
点位置画出x轴和y轴,建
立平面直角坐标系得到其他
点的坐标
在平面直角坐标系中,台阶可以看作弱化的网格,从中可以得到各个点的坐标,为进一步解题做好铺垫.
题型2 函数图象的实际意义
(2024·河北模拟)如图,李大爷在运动场上晨练,一段时间内沿着一扇形的周边(如图中箭头所示)的路径匀速小跑,能近似刻画李大爷离出发点A的距离y与时间x之间关系的函数图象是 ( )
A B
C D
考查函数图象的实际意义,如果单独考查,通常会出现在选择题中,如果结合函数性质考查,通常会出现在解答题中.关于运动变化速度的图象,是研究图象实际意义的基础.河北省在这个考点上的创新主要体现在三个方面:一是图象形式以散点方式呈现;二是问题情境力求新颖,不固守模式;三是与新的知识点综合.
一定要看清坐标轴所表示的意义,如果纵轴表示的是速度,那么与表示路程或距离的意义截然不同.
参考答案
考点清单
①> ②> ③< ④> ⑤< ⑥< ⑦> ⑧<
⑨相等 ⑩互为相反数 x+a y x+a
y+b |b| |a| 零 非负
基础演练
1.C 2.B 3.D 4.B
5.3 6.x≥且x≠3 7.(0,-2)
真题精粹·重变式
1.B
2.D 提示:根据已知,点P3(2,2)横、纵坐标之和除以3所得的余数为1,继而向上平移1个单位长度得到P4(2,3),此时横、纵坐标之和除以3所得的余数为2,继而向左平移1个单位长度得到P5(1,3),此时横、纵坐标之和除以3所得的余数为1,又向上平移1个单位长度……因此发现规律为若“和点”横、纵坐标之和除以3所得的余数为0时,先向右平移1个单位长度,再按照向上、向左,向上、向左不断重复的规律平移.
若“和点”Q按上述规则连续平移16次后,到达点Q16(-1,9),则按照“和点”Q16反向运动16次即可,可以分为两种情况:
①Q16(-1,9)先向右平移1个单位长度得到Q15(0,9),此时横、纵坐标之和除以3所得的余数为0,应该是Q15向右平移1个单位长度得到Q16,故矛盾,不成立;②Q16先向下平移1个单位长度得到Q15(-1,8),此时横、纵坐标之和除以3所得的余数为1,则应该向上平移1个单位得到Q16,故符合题意.
因此,点Q16先向下平移,再向右平移,当平移到第15次时,共计向下平移了8次,向右平移了7次,此时坐标为(-1+7,9-8),即(6,1),
∴最后一次若向右平移则为(7,1),若向左平移则为(5,1),
故选D.
3.D
核心突破·拓思维
例1
(1)建立平面直角坐标系如图所示.
(2)A(-4,-4),E(4,4),F(6,6).
(3)从点A开始,10级台阶水平方向的总长度=2×(10+1)=22,
到地面的距离=2×10=20.
根据勾股定理得到AM==2.
例2 C
提示:如图,当李大爷在半径AB上运动时,离出发点A的距离越来越远,即y随x的增大而增大;在上运动时,离点A的距离不变;在CA上运动时,离点A的距离越来越近,即y随x的增大而减小,故选C.
(6年3考,2~4分)
河北中考试卷中,会单独考查坐标平面内点的特征或规律,以及实际问题中函数图象的意义;也常把平面直角坐标系、函数概念与自变量取值范围、函数图象的知识,融入到一次函数、二次函数或反比例函数中,通过具体类型的函数进行考查,预计2025年对本节知识的考查,在选择题中以“独立式”为主,在解答题中以“融入式”为主.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1平面直角坐标系
相关概念1.定义:在平面内有公共原点且互相垂直的两条数轴构成平面直角坐标系. 2.几何意义:坐标平面内任意一点M与有序实数对(x,y)的关系是一一对应
点的坐标特征1.各象限内点的坐标的符号特征(如图所示): (1)点P(x,y)在第一象限 x① 0,y② 0, (2)点P(x,y)在第二象限 x③ 0,y④ 0, (3)点P(x,y)在第三象限 x⑤ 0,y⑥ 0, (4)点P(x,y)在第四象限 x⑦ 0,y⑧ 0. 【温馨提示】坐标轴上的点不属于任何象限. 2.坐标轴上点的坐标特征: (1)在横轴上 y=0. (2)在纵轴上 x=0. (3)原点 x=0,y=0
点的坐标 特征3.各象限角平分线上点的坐标: (1)第一、三象限角平分线上的点的横、纵坐标⑨ . (2)第二、四象限角平分线上的点的横、纵坐标⑩ . 4.点P(a,b)的对称点的坐标特征: (1)关于x轴对称的点P1的坐标为(a,-b). (2)关于y轴对称的点P2的坐标为(-a,b). (3)关于原点对称的点P3的坐标为(-a,-b). 5.点M(x,y)平移的坐标特征: M(x,y)M1( , )M2( , )
点的坐标 距离问题1.点M(a,b)到x轴,y轴的距离:到x轴的距离为 ;到y轴的距离为 ;到原点的距离为. 2.坐标轴上两点间的距离与平行于x轴,y轴直线上的两点间的距离: (1)点M1(x1,0),M2(x2,0)之间的距离为|x1-x2|. (2)点M1(x1,y),M2(x2,y)间的距离为|x1-x2|. (3)点M1(0,y1),M2(0,y2)间的距离为|y1-y2|. (4)点M1(x,y1),M2(x,y2)间的距离为|y1-y2|. 3.任意两点间的距离:点A(x1,y1),B(x2,y2)间的距离为
考点2函数
函数的相关概念1.常量、变量:在一个变化过程中,数值始终不变的量叫作常量,数值发生变化的量叫作变量. 2.函数:在一个变化过程中,有两个变量x和y,对于x的每一个值,y都有唯一确定的值与其对应,那么就称x是自变量,y是x的函数.函数的表示方法:列表法、图象法、解析式法. 3.函数自变量的取值范围:一般原则,整式为全体实数;分式的分母不为 ;二次根式的被开方数为 数;使实际问题有意义
函数的图象1.分析实际问题判断函数图象的方法: (1)找起点:结合题干中所给自变量及因变量的取值范围,对应到图象中找对应点. (2)找特殊点:即交点或转折点,说明图象在此点处将发生变化. (3)判断图象趋势:判断出函数的增减性,图象的倾斜方向. 2.画函数图象的步骤:列表、描点、连线
【基础演练】
1.(人教七下P84第1题变式)在平面直角坐标系中,第二象限内的点可能是 ( )
A.(1,2)
B.(1,-2)
C.(-1,2)
D.(-1,-2)
2.(人教七下P70第8题(2)变式)在平面直角坐标系中,直线AB平行于y轴,点A的坐标为(-3,2),点B的坐标可能为 ( )
A.(4,2) B.(-3,4)
C.(3,-4) D.(-4,2)
3.(冀教八下P40练习第2题变式)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 ( )
A.(-3,2) B.(-2,3)
C.(2,-3) D.(3,-2)
4.在平面直角坐标系中,点M(m-1,2m)在x轴上,则点M的坐标是 ( )
A.(1,0) B.(-1,0)
C.(0,2) D.(0,-1)
5.(冀教八下P39第1题变式)在平面直角坐标系中,点P(2,-3)到x轴的距离是 .
6.(冀教八下P67做一做第1题变式)函数y=的自变量x的取值范围是 .
7.全世界大约有19 000种蝴蝶,大部分分布在美洲,尤其在亚马孙河流域品种最多,在世界其他地区除了南北极寒冷地带以外都有分布.如图,这是一个蝴蝶标本,将其放在适当的平面直角坐标系中,若翅膀两端B,C两点的坐标分别为(-1,3),(3,0),则蝴蝶尾部点A的坐标为 .
真题精粹·重变式——河北6年真题精选及拓展
考向1平面直角坐标系 (6年2考)
1.(2024·河北12题2分)在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形ABCD位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是 ( )
A.点A B.点B
C.点C D.点D
2.(2024·河北16题2分)在平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.
例:“和点”P(2,1)按上述规则连续平移3次后,到达点P3(2,2),其平移过程如下:P1P2P3(2,2).
若“和点”Q按上述规则连续平移16次后,到达点Q16(-1,9),则点Q的坐标为 ( )
A.(6,1)或(7,1)
B.(15,-7)或(8,0)
C.(6,0)或(8,0)
D.(5,1)或(7,1)
考向2动点问题的函数图象 (6年1考)
3.(2023·河北14题2分)如图,这是一种轨道示意图,其中和均为半圆,点M,A,C,N依次在同一直线上,且AM=CN.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M→A→D→C→N和N→C→B→A→M.若移动时间为x,两个机器人之间的距离为y,则y与x之间的函数关系的图象大致是 ( )
A B
C D
核心突破·拓思维——学科核心素养提升
题型1 平面直角坐标系
(原创)如图,这是某台阶的一部分,点A与点B的水平距离以及每级台阶的水平、竖直距离都等于2,地面与x轴平行,点D的坐标为(2,2).
(1)请你在图中建立适当的平面直角坐标系.
(2)直接写出点A,E,F的坐标.
(3)如果台阶有10级(第11个点用M表示),请你求出该台阶到地面的距离和线段AM的长度.
由已知点求其他点的坐标的步骤
已知点的坐标确定原
点位置画出x轴和y轴,建
立平面直角坐标系得到其他
点的坐标
在平面直角坐标系中,台阶可以看作弱化的网格,从中可以得到各个点的坐标,为进一步解题做好铺垫.
题型2 函数图象的实际意义
(2024·河北模拟)如图,李大爷在运动场上晨练,一段时间内沿着一扇形的周边(如图中箭头所示)的路径匀速小跑,能近似刻画李大爷离出发点A的距离y与时间x之间关系的函数图象是 ( )
A B
C D
考查函数图象的实际意义,如果单独考查,通常会出现在选择题中,如果结合函数性质考查,通常会出现在解答题中.关于运动变化速度的图象,是研究图象实际意义的基础.河北省在这个考点上的创新主要体现在三个方面:一是图象形式以散点方式呈现;二是问题情境力求新颖,不固守模式;三是与新的知识点综合.
一定要看清坐标轴所表示的意义,如果纵轴表示的是速度,那么与表示路程或距离的意义截然不同.
参考答案
考点清单
①> ②> ③< ④> ⑤< ⑥< ⑦> ⑧<
⑨相等 ⑩互为相反数 x+a y x+a
y+b |b| |a| 零 非负
基础演练
1.C 2.B 3.D 4.B
5.3 6.x≥且x≠3 7.(0,-2)
真题精粹·重变式
1.B
2.D 提示:根据已知,点P3(2,2)横、纵坐标之和除以3所得的余数为1,继而向上平移1个单位长度得到P4(2,3),此时横、纵坐标之和除以3所得的余数为2,继而向左平移1个单位长度得到P5(1,3),此时横、纵坐标之和除以3所得的余数为1,又向上平移1个单位长度……因此发现规律为若“和点”横、纵坐标之和除以3所得的余数为0时,先向右平移1个单位长度,再按照向上、向左,向上、向左不断重复的规律平移.
若“和点”Q按上述规则连续平移16次后,到达点Q16(-1,9),则按照“和点”Q16反向运动16次即可,可以分为两种情况:
①Q16(-1,9)先向右平移1个单位长度得到Q15(0,9),此时横、纵坐标之和除以3所得的余数为0,应该是Q15向右平移1个单位长度得到Q16,故矛盾,不成立;②Q16先向下平移1个单位长度得到Q15(-1,8),此时横、纵坐标之和除以3所得的余数为1,则应该向上平移1个单位得到Q16,故符合题意.
因此,点Q16先向下平移,再向右平移,当平移到第15次时,共计向下平移了8次,向右平移了7次,此时坐标为(-1+7,9-8),即(6,1),
∴最后一次若向右平移则为(7,1),若向左平移则为(5,1),
故选D.
3.D
核心突破·拓思维
例1
(1)建立平面直角坐标系如图所示.
(2)A(-4,-4),E(4,4),F(6,6).
(3)从点A开始,10级台阶水平方向的总长度=2×(10+1)=22,
到地面的距离=2×10=20.
根据勾股定理得到AM==2.
例2 C
提示:如图,当李大爷在半径AB上运动时,离出发点A的距离越来越远,即y随x的增大而增大;在上运动时,离点A的距离不变;在CA上运动时,离点A的距离越来越近,即y随x的增大而减小,故选C.
同课章节目录
