【中考考点探究】第1节 圆的基本性质 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第1节 圆的基本性质 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:37:48 | ||
图片预览

文档简介
第1节 圆的基本性质
(6年3考,2分)
圆的基本性质的考查多以圆周角定理,垂径定理和弧、弦、圆心角之间的关系为主,一般以选择题和填空题的形式出现,也有一些简单的解答题,复习时一是要熟练掌握圆的相关定理和性质,二是要强化训练常考题型,举一反三.但随着新课程标准将垂径定理作为必学内容这一变化的出现,2023年和2024年在解答题中进行了重点考查,预测2025年的中考试题会更多体现新课标的理念.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1圆的有关概念 (轮考点)
定义 几何定义:圆是平面上到定点(圆心)的距离等于定长(半径)的点的集合,如图所示的圆记为☉O
旋转定义:圆也可以看作是一条线段绕其固定的一端点(圆心)旋转一周,其另一端点所描绘出的轨迹
弦与直径 连接圆上任意两点的线段(线段AD)叫作弦,过圆心的弦叫作直径(线段AB),直径是圆内① 的弦
弧 圆上任意两点间的部分叫作弧,小于半圆的弧叫② (如),大于半圆的弧叫③ (如)
等弧 同圆或等圆中,能够互相重合的弧
圆心角 顶点在圆心的角(如∠AOC)
圆周角 顶点在圆上,并且两边都与圆相交的角(如∠ADC)
弦心距 圆心到弦的距离(线段OE的长)
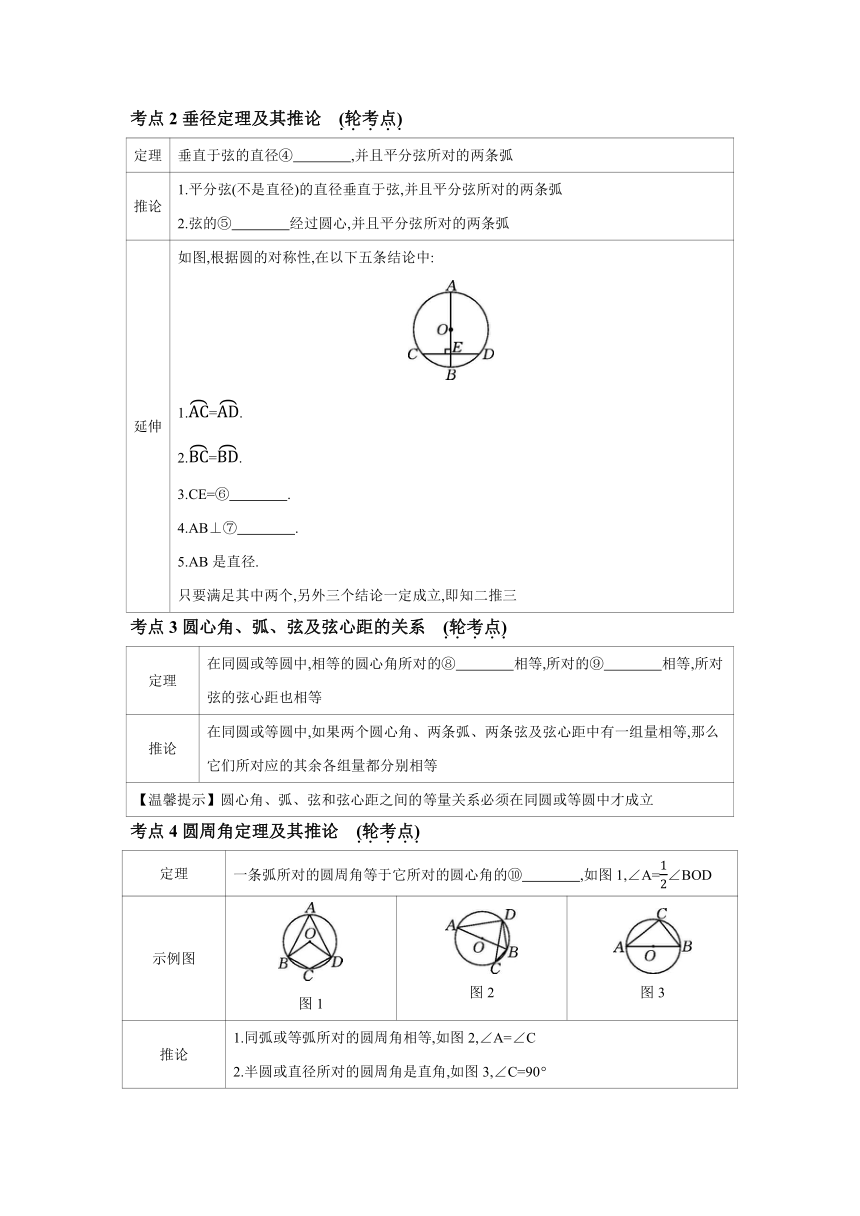
考点2垂径定理及其推论 (轮考点)
定理 垂直于弦的直径④ ,并且平分弦所对的两条弧
推论 1.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 2.弦的⑤ 经过圆心,并且平分弦所对的两条弧
延伸 如图,根据圆的对称性,在以下五条结论中: 1.=. 2.=. 3.CE=⑥ . 4.AB⊥⑦ . 5.AB是直径. 只要满足其中两个,另外三个结论一定成立,即知二推三
考点3圆心角、弧、弦及弦心距的关系 (轮考点)
定理 在同圆或等圆中,相等的圆心角所对的⑧ 相等,所对的⑨ 相等,所对弦的弦心距也相等
推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦及弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等
【温馨提示】圆心角、弧、弦和弦心距之间的等量关系必须在同圆或等圆中才成立
考点4圆周角定理及其推论 (轮考点)
定理 一条弧所对的圆周角等于它所对的圆心角的⑩ ,如图1,∠A=∠BOD
示例图 图1 图2 图3
推论 1.同弧或等弧所对的圆周角相等,如图2,∠A=∠C 2.半圆或直径所对的圆周角是直角,如图3,∠C=90°
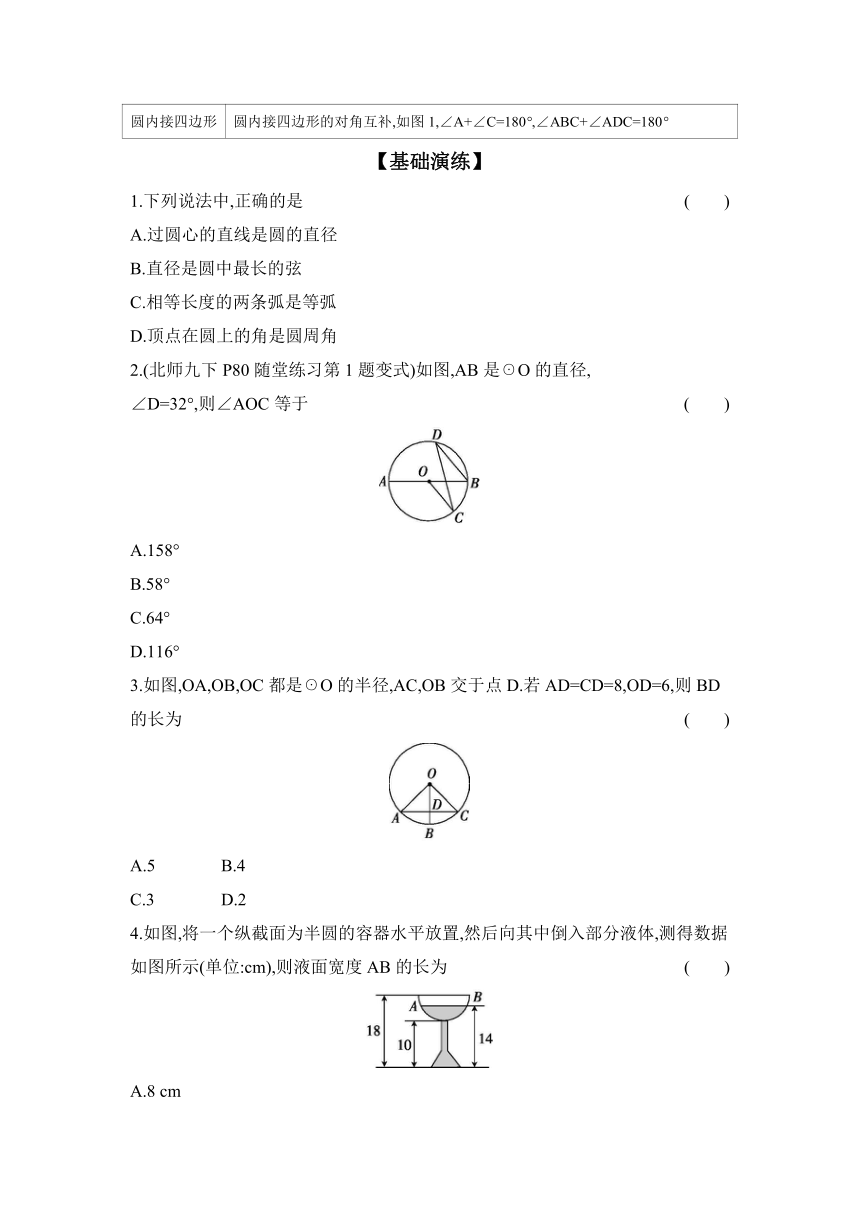
圆内接四边形 圆内接四边形的对角互补,如图1,∠A+∠C=180°,∠ABC+∠ADC=180°
【基础演练】
1.下列说法中,正确的是 ( )
A.过圆心的直线是圆的直径
B.直径是圆中最长的弦
C.相等长度的两条弧是等弧
D.顶点在圆上的角是圆周角
2.(北师九下P80随堂练习第1题变式)如图,AB是☉O的直径,
∠D=32°,则∠AOC等于 ( )
A.158°
B.58°
C.64°
D.116°
3.如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 ( )
A.5 B.4
C.3 D.2
4.如图,将一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图所示(单位:cm),则液面宽度AB的长为 ( )
A.8 cm
B.4 cm
C.4 cm
D.8 cm
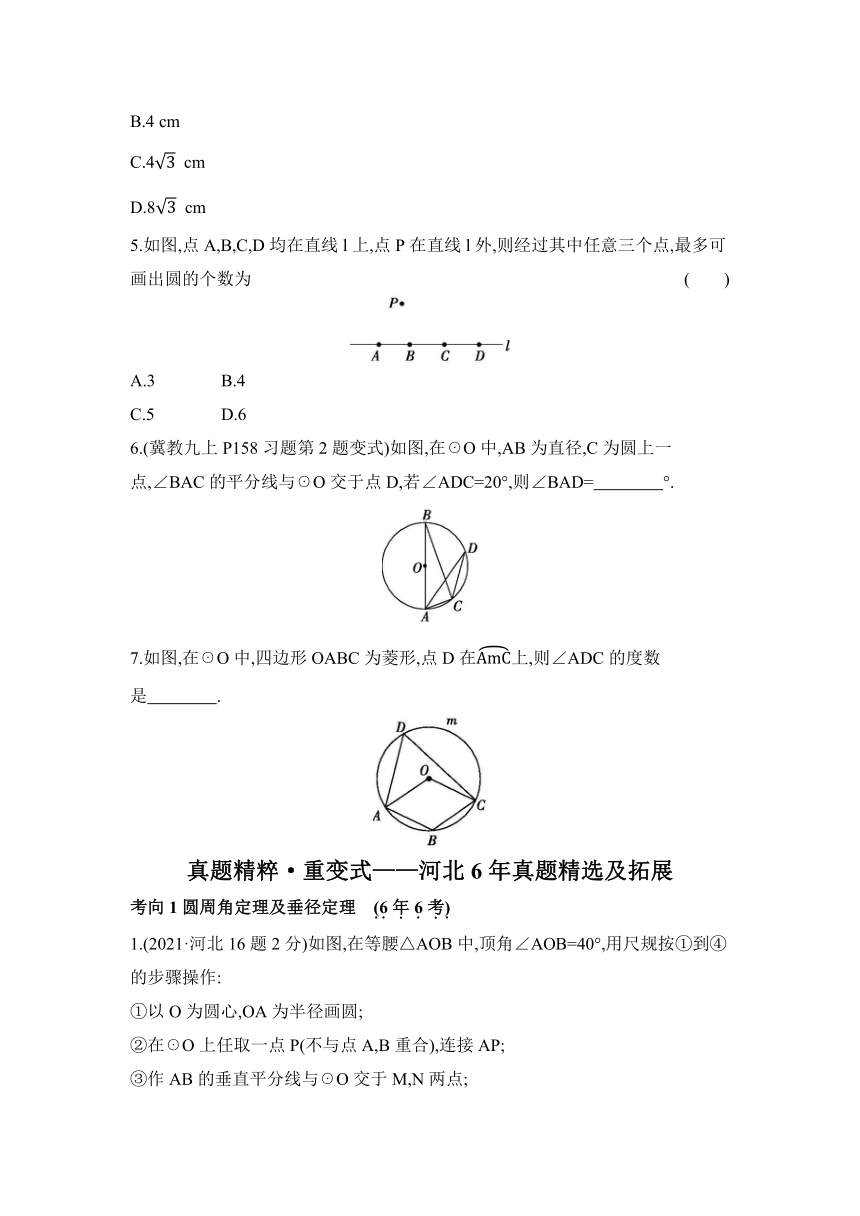
5.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为 ( )
A.3 B.4
C.5 D.6
6.(冀教九上P158习题第2题变式)如图,在☉O中,AB为直径,C为圆上一点,∠BAC的平分线与☉O交于点D,若∠ADC=20°,则∠BAD= °.
7.如图,在☉O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 .
真题精粹·重变式——河北6年真题精选及拓展
考向1圆周角定理及垂径定理 (6年6考)
1.(2021·河北16题2分)如图,在等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在☉O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与☉O交于M,N两点;
④作AP的垂直平分线与☉O交于E,F两点.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形.
结论Ⅱ:☉O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是 ( )
A.Ⅰ和Ⅱ都对
B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对
D.Ⅰ对Ⅱ不对
考向2垂径定理的实际应用 (6年2考)
2.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1 400年历史,是我国古代石拱桥的代表.图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26 m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5 m.连接OB.
(1)直接判断AD与BD的数量关系. (2)求这座石拱桥主桥拱的半径(精确到1 m).
核心突破·拓思维——学科核心素养提升
题型1 垂径定理及其推论
(2024·石家庄一模)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问径几何 ”用现在的几何语言表达为如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度是 ( )
A.12寸 B.24寸 C.13寸 D.26寸
垂径定理及其推论是基于圆的轴对称性质得到的一系列结论,在近年来的河北省中考中有时会与圆的其他知识综合考查,主要涉及计算类问题.除了常规问题外,几何计算类问题也常放置到实际问题的情境中,或结合中华优秀传统文化进行考查.
圆中常用辅助线口诀
圆的证明不算难,常把半径或弦连;有弦要想弦心距,它定垂直平分弦;
弧有中点圆心连,等弧对角要找全;作个直径再连弦,直角三角形定现.
题型2 与圆有关的角度计算
如图,量角器的直径与直角三角板ABC(∠BAC=30°)的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第8秒时,点E在量角器上对应的读数是 .
圆的很多基本性质与角度有关,比如圆周角与圆心角,圆内接四边形对角,直径所对的圆周角等,以及角与弧、弦的关系等,这些都能成为命题要素,既可以在选择题中单独考查,也可以放到圆的综合题中进行考查.
参考答案
考点清单
①最长 ②劣弧 ③优弧 ④平分这条弦
⑤垂直平分线 ⑥DE ⑦CD ⑧弧 ⑨弦 ⑩一半
基础演练
1.B 2.D 3.B 4.D 5.D
6.35 7.60°
真题精粹·重变式
1.D 提示:如图,连接EM,EN,MF,NF.
∵OM=ON,OE=OF,
∴四边形MENF是平行四边形.
∵EF=MN,∴四边形MENF是矩形,故Ⅰ正确.
观察图象可知,当∠MOF=∠AOB时,S扇形FOM=S扇形AOB,
观察图象可知,这样的点P不唯一,故Ⅱ错误,
故选D.
2.(1)∵OC⊥AB,∴AD=BD.
(2)设主桥拱的半径为R,由题意可知AB=26,CD=5,
∴BD=AB=13,
∴OD=OC-CD=R-5.
∵∠ODB=90°,∴OD2+BD2=OB2,
∴(R-5)2+132=R2,
解得R=19.4≈19.
答:这座石拱桥主桥拱的半径约为19 m.
核心突破·拓思维
例1D 提示:如图,连接OA.
∵AB⊥CD,且AB=10寸,由垂径定理,得AE=BE=5寸.
设圆O的半径OA的长为x,则OC=OD=x.
∵CE=1,∴OE=x-1.
在Rt△AOE中,根据勾股定理,得x2-(x-1)2=52,
化简,得x2-x2+2x-1=25,即2x=26,∴CD=26(寸),故选D.
例2
32° 提示:如图,连接OE.
∵∠ACB=90°,
∴点C在以AB为直径的圆上,即点C在☉O上,
∴∠EOA=2∠ECA.
∵∠ECA=2°×8=16°,
∴∠AOE=2∠ECA=2×16°=32°.
∵量角器0刻度线的端点N与点A重合,
∴点E在量角器上对应的读数是32°.
(6年3考,2分)
圆的基本性质的考查多以圆周角定理,垂径定理和弧、弦、圆心角之间的关系为主,一般以选择题和填空题的形式出现,也有一些简单的解答题,复习时一是要熟练掌握圆的相关定理和性质,二是要强化训练常考题型,举一反三.但随着新课程标准将垂径定理作为必学内容这一变化的出现,2023年和2024年在解答题中进行了重点考查,预测2025年的中考试题会更多体现新课标的理念.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1圆的有关概念 (轮考点)
定义 几何定义:圆是平面上到定点(圆心)的距离等于定长(半径)的点的集合,如图所示的圆记为☉O
旋转定义:圆也可以看作是一条线段绕其固定的一端点(圆心)旋转一周,其另一端点所描绘出的轨迹
弦与直径 连接圆上任意两点的线段(线段AD)叫作弦,过圆心的弦叫作直径(线段AB),直径是圆内① 的弦
弧 圆上任意两点间的部分叫作弧,小于半圆的弧叫② (如),大于半圆的弧叫③ (如)
等弧 同圆或等圆中,能够互相重合的弧
圆心角 顶点在圆心的角(如∠AOC)
圆周角 顶点在圆上,并且两边都与圆相交的角(如∠ADC)
弦心距 圆心到弦的距离(线段OE的长)
考点2垂径定理及其推论 (轮考点)
定理 垂直于弦的直径④ ,并且平分弦所对的两条弧
推论 1.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 2.弦的⑤ 经过圆心,并且平分弦所对的两条弧
延伸 如图,根据圆的对称性,在以下五条结论中: 1.=. 2.=. 3.CE=⑥ . 4.AB⊥⑦ . 5.AB是直径. 只要满足其中两个,另外三个结论一定成立,即知二推三
考点3圆心角、弧、弦及弦心距的关系 (轮考点)
定理 在同圆或等圆中,相等的圆心角所对的⑧ 相等,所对的⑨ 相等,所对弦的弦心距也相等
推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦及弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等
【温馨提示】圆心角、弧、弦和弦心距之间的等量关系必须在同圆或等圆中才成立
考点4圆周角定理及其推论 (轮考点)
定理 一条弧所对的圆周角等于它所对的圆心角的⑩ ,如图1,∠A=∠BOD
示例图 图1 图2 图3
推论 1.同弧或等弧所对的圆周角相等,如图2,∠A=∠C 2.半圆或直径所对的圆周角是直角,如图3,∠C=90°
圆内接四边形 圆内接四边形的对角互补,如图1,∠A+∠C=180°,∠ABC+∠ADC=180°
【基础演练】
1.下列说法中,正确的是 ( )
A.过圆心的直线是圆的直径
B.直径是圆中最长的弦
C.相等长度的两条弧是等弧
D.顶点在圆上的角是圆周角
2.(北师九下P80随堂练习第1题变式)如图,AB是☉O的直径,
∠D=32°,则∠AOC等于 ( )
A.158°
B.58°
C.64°
D.116°
3.如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 ( )
A.5 B.4
C.3 D.2
4.如图,将一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图所示(单位:cm),则液面宽度AB的长为 ( )
A.8 cm
B.4 cm
C.4 cm
D.8 cm
5.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为 ( )
A.3 B.4
C.5 D.6
6.(冀教九上P158习题第2题变式)如图,在☉O中,AB为直径,C为圆上一点,∠BAC的平分线与☉O交于点D,若∠ADC=20°,则∠BAD= °.
7.如图,在☉O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 .
真题精粹·重变式——河北6年真题精选及拓展
考向1圆周角定理及垂径定理 (6年6考)
1.(2021·河北16题2分)如图,在等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在☉O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与☉O交于M,N两点;
④作AP的垂直平分线与☉O交于E,F两点.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形.
结论Ⅱ:☉O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是 ( )
A.Ⅰ和Ⅱ都对
B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对
D.Ⅰ对Ⅱ不对
考向2垂径定理的实际应用 (6年2考)
2.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1 400年历史,是我国古代石拱桥的代表.图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26 m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5 m.连接OB.
(1)直接判断AD与BD的数量关系. (2)求这座石拱桥主桥拱的半径(精确到1 m).
核心突破·拓思维——学科核心素养提升
题型1 垂径定理及其推论
(2024·石家庄一模)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问径几何 ”用现在的几何语言表达为如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度是 ( )
A.12寸 B.24寸 C.13寸 D.26寸
垂径定理及其推论是基于圆的轴对称性质得到的一系列结论,在近年来的河北省中考中有时会与圆的其他知识综合考查,主要涉及计算类问题.除了常规问题外,几何计算类问题也常放置到实际问题的情境中,或结合中华优秀传统文化进行考查.
圆中常用辅助线口诀
圆的证明不算难,常把半径或弦连;有弦要想弦心距,它定垂直平分弦;
弧有中点圆心连,等弧对角要找全;作个直径再连弦,直角三角形定现.
题型2 与圆有关的角度计算
如图,量角器的直径与直角三角板ABC(∠BAC=30°)的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第8秒时,点E在量角器上对应的读数是 .
圆的很多基本性质与角度有关,比如圆周角与圆心角,圆内接四边形对角,直径所对的圆周角等,以及角与弧、弦的关系等,这些都能成为命题要素,既可以在选择题中单独考查,也可以放到圆的综合题中进行考查.
参考答案
考点清单
①最长 ②劣弧 ③优弧 ④平分这条弦
⑤垂直平分线 ⑥DE ⑦CD ⑧弧 ⑨弦 ⑩一半
基础演练
1.B 2.D 3.B 4.D 5.D
6.35 7.60°
真题精粹·重变式
1.D 提示:如图,连接EM,EN,MF,NF.
∵OM=ON,OE=OF,
∴四边形MENF是平行四边形.
∵EF=MN,∴四边形MENF是矩形,故Ⅰ正确.
观察图象可知,当∠MOF=∠AOB时,S扇形FOM=S扇形AOB,
观察图象可知,这样的点P不唯一,故Ⅱ错误,
故选D.
2.(1)∵OC⊥AB,∴AD=BD.
(2)设主桥拱的半径为R,由题意可知AB=26,CD=5,
∴BD=AB=13,
∴OD=OC-CD=R-5.
∵∠ODB=90°,∴OD2+BD2=OB2,
∴(R-5)2+132=R2,
解得R=19.4≈19.
答:这座石拱桥主桥拱的半径约为19 m.
核心突破·拓思维
例1D 提示:如图,连接OA.
∵AB⊥CD,且AB=10寸,由垂径定理,得AE=BE=5寸.
设圆O的半径OA的长为x,则OC=OD=x.
∵CE=1,∴OE=x-1.
在Rt△AOE中,根据勾股定理,得x2-(x-1)2=52,
化简,得x2-x2+2x-1=25,即2x=26,∴CD=26(寸),故选D.
例2
32° 提示:如图,连接OE.
∵∠ACB=90°,
∴点C在以AB为直径的圆上,即点C在☉O上,
∴∠EOA=2∠ECA.
∵∠ECA=2°×8=16°,
∴∠AOE=2∠ECA=2×16°=32°.
∵量角器0刻度线的端点N与点A重合,
∴点E在量角器上对应的读数是32°.
同课章节目录
