【中考考点探究】第1节 统计 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第1节 统计 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.1KB | ||
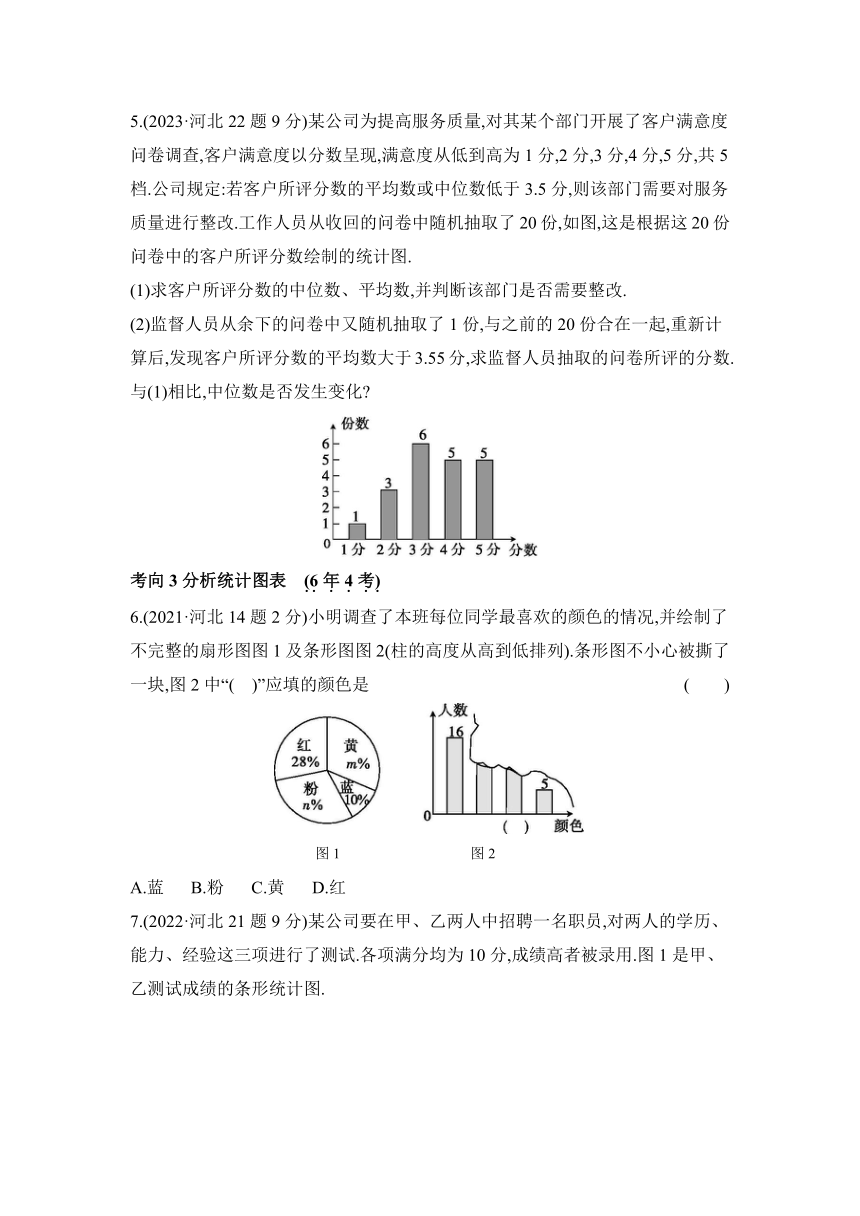
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:38:35 | ||
图片预览




文档简介
第1节 统计
(6年13考,5~13分)
统计是河北省中考的必考内容,主要涉及统计图表与统计量,重点是对统计图表中数据信息的分析,以及各统计量的计算方法和实际意义,并根据统计量进行说理推断.2019年以来,对不完整统计图的考查有所弱化,在2024年的解答题中甚至没有出现统计图.预测2025年的河北省中考试题中,仍然考查统计量的计算,不会出现不完整统计图.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1数据的收集
数据收集的常用方法 1.① :考察全体对象的调查,一般调查对象的范围小、不具有破坏性、数据要求准确、全面时,适用全面调查,如乘飞机安检. 2.② :抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,当所调查对象涉及面大、范围广、受条件限制或具有破坏性等时,适用抽样调查,如调查中学生对数学文化的了解情况
数据收集时常见的统计量 1.总体:所考察对象的③ . 2.个体:组成④ 的每一个考察对象. 3.样本:总体中被抽取的⑤ . 4.样本容量:样本中包含个体的数目
考点2反映数据集中程度的量 (常考点)
算术平均数 x1,x2,…,xn的平均数=⑥
加权平均数 (1)一般地,若n个数x1,x2,…,xn的权分别是ω1,ω2,…,ωn,则叫作这n个数的加权平均数. (2)若x1出现f1次,x2出现f2次,…,xk出现fk次,且f1+f2+…+fk=n,则这k个数的加权平均数=(x1f1+x2f2+…+xkfk)
中位数 一组数据按⑦ 的顺序排列,若数据的个数是⑧ ,则称处于中间位置的数为这组数据的中位数;若数据的个数是⑨ ,则称中间两个数据的平均数为这组数据的中位数
众数 一组数据中出现次数⑩ 的数据,一组数据的众数可能有多个,也可能没有
考点3反映数据离散程度的量
方差 方差公式 设x1,x2,…,xn的平均数为,则这n个数据的方差为s2=[(x1-)2+(x2-)2+…+(xn-)2]
方差的意义 方差越大,数据的波动 ;方差越小,数据的波动 ,越稳定
考点4数据的整理和描述 (常考点)
频数 数据分组后落在各小组内数据的个数,频数之和等于数据总数
频率 每一组数据频数与数据总数的比
统计图 条形统计图 能够显示每组中的具体数据,易于比较数据之间的差别
扇形统计图 能够显示部分在总体中的 ,易于显示每组数据相对于总数的大小
折线统计图 可以表示出数量的多少,易于显示数据的
频数分布直方图 清楚显示各组频数分布情况,易于显示各组之间频数的差别
【基础演练】
1.空气是混合物,为直观介绍空气中各成分的百分比,所采用的统计图最适合的是 ( )
A.折线统计图 B.扇形统计图
C.频数分布直方图 D.条形统计图
2.(冀教八下P7组第1题变式)为了解某校3 000名学生每天的阅读时间,从中抽取100名学生进行调查,其中的100是 ( )
A.总体 B.个体
C.样本 D.样本容量
3.(人教七下P140练习第3题变式)下面调查中,适合采用全面调查的是 ( )
A.了解冷饮市场上光明冰砖的质量情况
B.了解市面上一次性餐盒的卫生情况
C.了解一个班级学生的视力情况
D.了解某型号手机的使用寿命
4.某中学学生会想要统计最受本校学生欢迎的春运会运动项目,以下是打乱的统计步骤:①根据统计表绘制条形统计图.②制作调查问卷,对全校学生进行问卷调查.③从条形统计图中分析出最受欢迎的春运会项目.④整理问卷调查数据并绘制统计表.统计步骤的正确排列顺序为 ( )
A.④③②① B.②④①③
C.②①③④ D.②④③①
5.(人教八下P113第2题变式)某县举行朗诵比赛,将朗诵技巧、表现技巧、创新亮点三个方面分别按50%,40%,10%的比例计入总分.小华各项得分如表所示,则小华的最终得分为 ( )
评分内容 朗诵技巧 表现技巧 创新亮点
得分 90分 85分 95分
A.90分 B.89分
C.88.5分 D.88分
6.对于一组统计数据:2,2,3,4,4.下列说法错误的是 ( )
A.平均数是3 B.方差是0.8
C.中位数是3 D.众数是4
真题精粹·重变式——河北6年真题精选及拓展
考向1统计步骤 (6年1考)
1.(2019·河北11题2分)某同学要统计本校图书馆中最受学生欢迎的图书种类,以下是打乱的统计步骤:①从扇形图中分析出最受学生欢迎的图书种类;②去图书馆收集学生借阅图书的记录;③绘制扇形图来表示各个种类所占的百分比;④整理借阅图书记录并绘制频数分布表.正确的统计步骤是 ( )
A.②→③→①→④
B.③→④→①→②
C.①→②→④→③
D.②→④→③→①
考向2平均数、中位数、众数、方差的计算及意义 (6年8考)
2.(2020·河北5题3分)如图,这是小颖前三次购买苹果单价的统计图,第四次购买的苹果单价是a元,发现这四个单价的中位数恰好也是众数,则a的值为 ( )
A.9 B.8 C.7 D.6
3.(2022·河北14题2分)五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,其中趋势相同的是 ( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
4.(2024·河北17题2分)某校生物小组的9名同学各用100粒种子做发芽试验,几天后观察并记录种子的发芽数分别为89,73,90,86,75,86,89,95,89,以上数据的众数为 .
5.(2023·河北22题9分)某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,如图,这是根据这20份问卷中的客户所评分数绘制的统计图.
(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改.
(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评的分数.与(1)相比,中位数是否发生变化
考向3分析统计图表 (6年4考)
6.(2021·河北14题2分)小明调查了本班每位同学最喜欢的颜色的情况,并绘制了不完整的扇形图图1及条形图图2(柱的高度从高到低排列).条形图不小心被撕了一块,图2中“( )”应填的颜色是 ( )
图1 图2
A.蓝 B.粉 C.黄 D.红
7.(2022·河北21题9分)某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试.各项满分均为10分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图.
(1)分别求出甲、乙三项成绩之和,并指出会录用谁.
(2)若将甲、乙的三项测试成绩,按照扇形统计图(如图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.
核心突破·拓思维——学科核心素养提升
题型1 统计量的计算
(2024·唐山一模)老师在黑板上写出一个计算方差的算式:s2=[(10-7.8)2+(9-7.8)2+(8-7.8)2+2×(6-7.8)2],根据上式还原得到的数据,下列结论不正确的是 ( )
A.n=5
B.平均数为7.8
C.添加一个数7.8后方差不变
D.这组数据的众数是6
方差公式剖析
题型2 依据统计图表分析数据
(2024 邢台一模)温室内,经过一段时间育苗,随机抽取一些种苗并对它们的株高进行测量,把测量结果制成尚不完整的扇形统计图与条形统计图.如图,若种苗株高的平均数或中位数低于12 cm,则需要对育苗办法进行适当调整.
(1)在扇形统计图中,m= .
根据方差公式中各部分的意义找出原始数据及其平均数
↓
找出出现次数最多的数,即众数
↓
比较添加数据前后方差算式的结构特征,推测结果是否变化
↓
根据计算结果进行判断,得到符合题意的选项
河北省在解答题中经常考查统计图,如果出现两个统计图,则通常包含不完整的项目.常见的命题角度,一是要求根据统计图确定原始数据,补全统计图中的图形、数据或项目;二是计算统计量,并根据统计量的意义进行说理比较或者决策判断;三是通过统计量是否改变以及如何改变,考查原始数据的变化范围;四是用样本估计总体,推测总体的情况.
(2)求抽取的种苗株高的平均数、中位数,并判断是否需要对育苗方法进行调整.
(3)若再随机抽取n株种苗,对其高度进行测量,并与前面抽取的种苗株高合在一起,发现中位数变大,求n的最小值.
统计图表问题解题路线图
参考答案
考点清单
①全面调查 ②抽样调查 ③全体 ④总体
⑤一部分个体 ⑥(x1+x2+…+xn)
⑦从小到大(或从大到小) ⑧奇数 ⑨偶数 ⑩最多
越大 越小 百分比 变化趋势
基础演练
1.B 2.D 3.C 4.B 5.C 6.D
真题精粹·重变式
1.D
2.B 提示:由统计图可知,前三次的中位数是8.
∵第四次购买的苹果单价是a元,这四个单价的中位数恰好也是众数,
∴众数是前三次苹果单价中的一个,且与中位数相同,则a=8,故选B.
3.D
4.89
5.(1)由条形图可知,第10个数据是3分,第11个数据是4分,
∴中位数为3.5分.
由统计图可得平均数为
=3.5(分),
∴客户所评分数的平均数或中位数都不低于3.5分,
∴该部门不需要整改.
(2)设监督人员抽取的问卷所评分数为x分,
则有>3.55,
解得x>4.55.
∵满意度从低到高为1分,2分,3分,4分,5分,共5档,
∴监督人员抽取的问卷所评分数为5分.
∵4<5,
∴加入这个数据,客户所评分数按从小到大排列后,第11个数据不变还是4分,即加入这个数据后,中位数是4分,
∴与(1)相比,中位数发生了变化,由3.5分变成4分.
6.D 提示:本班一共有5÷10%=50(人),16人占×100%=32%,
∴喜欢红色的人数是50×28%=14(人),还有50-16-5-14=15(人).
∵柱的高度从高到低排列,对应人数依次为16,15,14,5,
∴图2中“( )”应填的颜色是红色,故选D.
7.(1)由题意得甲三项成绩之和为9+5+9=23(分),
乙三项成绩之和为8+9+5=22(分).
∵23>22,∴会录用甲.
(2)由题意得,甲三项成绩的加权平均数为
9×+5×+9×=3+2.5+1.5=7(分),
乙三项成绩的加权平均数为
8×+9×+5×=+4.5+=8(分).
∵7<8,会录用乙,∴会改变(1)的录用结果.
核心突破·拓思维
例1C 提示:由计算方差的算式可知,
数据个数n=1+1+1+2=5,
这组数据分别为10,9,8,6,6,
这组数据的平均数是7.8,
这组数据的众数是6,
添加一个数7.8后,计算方差的算式变为s2=×[(10-7.8)2+(9-7.8)2+(8-7.8)2+2×(6-7.8)2+(7.8-7.8)2],
=×[(10-7.8)2+(9-7.8)2+(8-7.8)2+2×(6-7.8)2]
中括号内的计算结果不变,前面的分数由变为,导致s2的值变小了.
综上分析,A,B,D的结论正确,C的结论不正确.故选C.
例2(1)20.
提示:m%=100%-25%-10%-10%-35%=20%,
所以m=20.
故答案为20.
(2)抽取种苗的总株数为14÷35%=40,
株高为12 cm的种苗株数为40×25%=10,
株高为13 cm的种苗株数为40×10%=4,
∴抽取的种苗株高的平均数
==11.4(cm).
∵将抽取的40个数据从小到大排列,处于第20,21个的均为11 cm,
∴中位数为=11(cm).
∵种苗株高的平均数和中位数均低于12 cm,
∴需要对育苗办法进行适当调整.
(3)将抽取的40个数据从小到大排列,发现处于第22,23个的分别为11 cm,12 cm,
要使再随机抽取n株种苗后中位数变大,则株高均大于或等于12 cm,且n的最小值为22×2-40=4,
此时中位数为=11.5.
(6年13考,5~13分)
统计是河北省中考的必考内容,主要涉及统计图表与统计量,重点是对统计图表中数据信息的分析,以及各统计量的计算方法和实际意义,并根据统计量进行说理推断.2019年以来,对不完整统计图的考查有所弱化,在2024年的解答题中甚至没有出现统计图.预测2025年的河北省中考试题中,仍然考查统计量的计算,不会出现不完整统计图.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1数据的收集
数据收集的常用方法 1.① :考察全体对象的调查,一般调查对象的范围小、不具有破坏性、数据要求准确、全面时,适用全面调查,如乘飞机安检. 2.② :抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,当所调查对象涉及面大、范围广、受条件限制或具有破坏性等时,适用抽样调查,如调查中学生对数学文化的了解情况
数据收集时常见的统计量 1.总体:所考察对象的③ . 2.个体:组成④ 的每一个考察对象. 3.样本:总体中被抽取的⑤ . 4.样本容量:样本中包含个体的数目
考点2反映数据集中程度的量 (常考点)
算术平均数 x1,x2,…,xn的平均数=⑥
加权平均数 (1)一般地,若n个数x1,x2,…,xn的权分别是ω1,ω2,…,ωn,则叫作这n个数的加权平均数. (2)若x1出现f1次,x2出现f2次,…,xk出现fk次,且f1+f2+…+fk=n,则这k个数的加权平均数=(x1f1+x2f2+…+xkfk)
中位数 一组数据按⑦ 的顺序排列,若数据的个数是⑧ ,则称处于中间位置的数为这组数据的中位数;若数据的个数是⑨ ,则称中间两个数据的平均数为这组数据的中位数
众数 一组数据中出现次数⑩ 的数据,一组数据的众数可能有多个,也可能没有
考点3反映数据离散程度的量
方差 方差公式 设x1,x2,…,xn的平均数为,则这n个数据的方差为s2=[(x1-)2+(x2-)2+…+(xn-)2]
方差的意义 方差越大,数据的波动 ;方差越小,数据的波动 ,越稳定
考点4数据的整理和描述 (常考点)
频数 数据分组后落在各小组内数据的个数,频数之和等于数据总数
频率 每一组数据频数与数据总数的比
统计图 条形统计图 能够显示每组中的具体数据,易于比较数据之间的差别
扇形统计图 能够显示部分在总体中的 ,易于显示每组数据相对于总数的大小
折线统计图 可以表示出数量的多少,易于显示数据的
频数分布直方图 清楚显示各组频数分布情况,易于显示各组之间频数的差别
【基础演练】
1.空气是混合物,为直观介绍空气中各成分的百分比,所采用的统计图最适合的是 ( )
A.折线统计图 B.扇形统计图
C.频数分布直方图 D.条形统计图
2.(冀教八下P7组第1题变式)为了解某校3 000名学生每天的阅读时间,从中抽取100名学生进行调查,其中的100是 ( )
A.总体 B.个体
C.样本 D.样本容量
3.(人教七下P140练习第3题变式)下面调查中,适合采用全面调查的是 ( )
A.了解冷饮市场上光明冰砖的质量情况
B.了解市面上一次性餐盒的卫生情况
C.了解一个班级学生的视力情况
D.了解某型号手机的使用寿命
4.某中学学生会想要统计最受本校学生欢迎的春运会运动项目,以下是打乱的统计步骤:①根据统计表绘制条形统计图.②制作调查问卷,对全校学生进行问卷调查.③从条形统计图中分析出最受欢迎的春运会项目.④整理问卷调查数据并绘制统计表.统计步骤的正确排列顺序为 ( )
A.④③②① B.②④①③
C.②①③④ D.②④③①
5.(人教八下P113第2题变式)某县举行朗诵比赛,将朗诵技巧、表现技巧、创新亮点三个方面分别按50%,40%,10%的比例计入总分.小华各项得分如表所示,则小华的最终得分为 ( )
评分内容 朗诵技巧 表现技巧 创新亮点
得分 90分 85分 95分
A.90分 B.89分
C.88.5分 D.88分
6.对于一组统计数据:2,2,3,4,4.下列说法错误的是 ( )
A.平均数是3 B.方差是0.8
C.中位数是3 D.众数是4
真题精粹·重变式——河北6年真题精选及拓展
考向1统计步骤 (6年1考)
1.(2019·河北11题2分)某同学要统计本校图书馆中最受学生欢迎的图书种类,以下是打乱的统计步骤:①从扇形图中分析出最受学生欢迎的图书种类;②去图书馆收集学生借阅图书的记录;③绘制扇形图来表示各个种类所占的百分比;④整理借阅图书记录并绘制频数分布表.正确的统计步骤是 ( )
A.②→③→①→④
B.③→④→①→②
C.①→②→④→③
D.②→④→③→①
考向2平均数、中位数、众数、方差的计算及意义 (6年8考)
2.(2020·河北5题3分)如图,这是小颖前三次购买苹果单价的统计图,第四次购买的苹果单价是a元,发现这四个单价的中位数恰好也是众数,则a的值为 ( )
A.9 B.8 C.7 D.6
3.(2022·河北14题2分)五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,其中趋势相同的是 ( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
4.(2024·河北17题2分)某校生物小组的9名同学各用100粒种子做发芽试验,几天后观察并记录种子的发芽数分别为89,73,90,86,75,86,89,95,89,以上数据的众数为 .
5.(2023·河北22题9分)某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,如图,这是根据这20份问卷中的客户所评分数绘制的统计图.
(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改.
(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评的分数.与(1)相比,中位数是否发生变化
考向3分析统计图表 (6年4考)
6.(2021·河北14题2分)小明调查了本班每位同学最喜欢的颜色的情况,并绘制了不完整的扇形图图1及条形图图2(柱的高度从高到低排列).条形图不小心被撕了一块,图2中“( )”应填的颜色是 ( )
图1 图2
A.蓝 B.粉 C.黄 D.红
7.(2022·河北21题9分)某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试.各项满分均为10分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图.
(1)分别求出甲、乙三项成绩之和,并指出会录用谁.
(2)若将甲、乙的三项测试成绩,按照扇形统计图(如图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.
核心突破·拓思维——学科核心素养提升
题型1 统计量的计算
(2024·唐山一模)老师在黑板上写出一个计算方差的算式:s2=[(10-7.8)2+(9-7.8)2+(8-7.8)2+2×(6-7.8)2],根据上式还原得到的数据,下列结论不正确的是 ( )
A.n=5
B.平均数为7.8
C.添加一个数7.8后方差不变
D.这组数据的众数是6
方差公式剖析
题型2 依据统计图表分析数据
(2024 邢台一模)温室内,经过一段时间育苗,随机抽取一些种苗并对它们的株高进行测量,把测量结果制成尚不完整的扇形统计图与条形统计图.如图,若种苗株高的平均数或中位数低于12 cm,则需要对育苗办法进行适当调整.
(1)在扇形统计图中,m= .
根据方差公式中各部分的意义找出原始数据及其平均数
↓
找出出现次数最多的数,即众数
↓
比较添加数据前后方差算式的结构特征,推测结果是否变化
↓
根据计算结果进行判断,得到符合题意的选项
河北省在解答题中经常考查统计图,如果出现两个统计图,则通常包含不完整的项目.常见的命题角度,一是要求根据统计图确定原始数据,补全统计图中的图形、数据或项目;二是计算统计量,并根据统计量的意义进行说理比较或者决策判断;三是通过统计量是否改变以及如何改变,考查原始数据的变化范围;四是用样本估计总体,推测总体的情况.
(2)求抽取的种苗株高的平均数、中位数,并判断是否需要对育苗方法进行调整.
(3)若再随机抽取n株种苗,对其高度进行测量,并与前面抽取的种苗株高合在一起,发现中位数变大,求n的最小值.
统计图表问题解题路线图
参考答案
考点清单
①全面调查 ②抽样调查 ③全体 ④总体
⑤一部分个体 ⑥(x1+x2+…+xn)
⑦从小到大(或从大到小) ⑧奇数 ⑨偶数 ⑩最多
越大 越小 百分比 变化趋势
基础演练
1.B 2.D 3.C 4.B 5.C 6.D
真题精粹·重变式
1.D
2.B 提示:由统计图可知,前三次的中位数是8.
∵第四次购买的苹果单价是a元,这四个单价的中位数恰好也是众数,
∴众数是前三次苹果单价中的一个,且与中位数相同,则a=8,故选B.
3.D
4.89
5.(1)由条形图可知,第10个数据是3分,第11个数据是4分,
∴中位数为3.5分.
由统计图可得平均数为
=3.5(分),
∴客户所评分数的平均数或中位数都不低于3.5分,
∴该部门不需要整改.
(2)设监督人员抽取的问卷所评分数为x分,
则有>3.55,
解得x>4.55.
∵满意度从低到高为1分,2分,3分,4分,5分,共5档,
∴监督人员抽取的问卷所评分数为5分.
∵4<5,
∴加入这个数据,客户所评分数按从小到大排列后,第11个数据不变还是4分,即加入这个数据后,中位数是4分,
∴与(1)相比,中位数发生了变化,由3.5分变成4分.
6.D 提示:本班一共有5÷10%=50(人),16人占×100%=32%,
∴喜欢红色的人数是50×28%=14(人),还有50-16-5-14=15(人).
∵柱的高度从高到低排列,对应人数依次为16,15,14,5,
∴图2中“( )”应填的颜色是红色,故选D.
7.(1)由题意得甲三项成绩之和为9+5+9=23(分),
乙三项成绩之和为8+9+5=22(分).
∵23>22,∴会录用甲.
(2)由题意得,甲三项成绩的加权平均数为
9×+5×+9×=3+2.5+1.5=7(分),
乙三项成绩的加权平均数为
8×+9×+5×=+4.5+=8(分).
∵7<8,会录用乙,∴会改变(1)的录用结果.
核心突破·拓思维
例1C 提示:由计算方差的算式可知,
数据个数n=1+1+1+2=5,
这组数据分别为10,9,8,6,6,
这组数据的平均数是7.8,
这组数据的众数是6,
添加一个数7.8后,计算方差的算式变为s2=×[(10-7.8)2+(9-7.8)2+(8-7.8)2+2×(6-7.8)2+(7.8-7.8)2],
=×[(10-7.8)2+(9-7.8)2+(8-7.8)2+2×(6-7.8)2]
中括号内的计算结果不变,前面的分数由变为,导致s2的值变小了.
综上分析,A,B,D的结论正确,C的结论不正确.故选C.
例2(1)20.
提示:m%=100%-25%-10%-10%-35%=20%,
所以m=20.
故答案为20.
(2)抽取种苗的总株数为14÷35%=40,
株高为12 cm的种苗株数为40×25%=10,
株高为13 cm的种苗株数为40×10%=4,
∴抽取的种苗株高的平均数
==11.4(cm).
∵将抽取的40个数据从小到大排列,处于第20,21个的均为11 cm,
∴中位数为=11(cm).
∵种苗株高的平均数和中位数均低于12 cm,
∴需要对育苗办法进行适当调整.
(3)将抽取的40个数据从小到大排列,发现处于第22,23个的分别为11 cm,12 cm,
要使再随机抽取n株种苗后中位数变大,则株高均大于或等于12 cm,且n的最小值为22×2-40=4,
此时中位数为=11.5.
同课章节目录
