【中考考点探究】第2节 三角形与特殊三角形 第2讲 等腰三角形与直角三角形 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第2节 三角形与特殊三角形 第2讲 等腰三角形与直角三角形 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 308.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:38:43 | ||
图片预览




文档简介
第2讲 等腰三角形与直角三角形
(6年15考,2~7分)
等腰三角形和直角三角形主要考查等腰、等边和直角三角形的性质与判定,常见辅助线的作法以及分类讨论思想的应用.从难易度上分为两类,第一类以简单的计算或证明为主,第二类以等腰三角形或直角三角形为图形背景考查几何证明与计算.河北省中考一般作为背景考查,预计2025年仍将延续.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1等腰三角形的性质与判定 (常考点)
性质 1.等边对等角:两腰相等,两① 相等. 2.“三线合一”:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. 3.对称性:等腰三角形是轴对称图形,有② 条对称轴
判定 1.有两边相等的三角形是等腰三角形. 2.有两角相等的三角形是等腰三角形(等角对等边)
考点2等边三角形的性质与判定
性质1.边角关系:三边相等,三个内角相等且都等于③ . 2.“三线合一”:任意一边上的高、中线及其对角的平分线互相重合. 3.对称性:等边三角形是轴对称图形,三条高(或角平分线或中线)所在的直线是对称轴
判定1.定义:三边都相等的三角形是等边三角形. 2.三个角都相等(均为60°)的三角形是等边三角形. 3.有一个角为60°的④ 三角形是等边三角形
考点3直角三角形的性质与判定 (常考点)
性质1.两锐角互余. 2.30°角所对的直角边等于斜边的一半. 3.斜边上的中线等于斜边的⑤ . 4.勾股定理:两直角边a,b的平方和等于斜边c的平方,即⑥ . 5.在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于⑦
判定1.有一个角为90°的三角形是直角三角形. 2.两个锐角互为⑧ 的三角形是直角三角形. 3.勾股定理逆定理:已知三角形的边长分别为a,b,c,若a2+b2=c2,则这个三角形是直角三角形
【基础演练】
1.(人教八上P77第2题变式)如图,△ABC是等腰三角形,AB=AC,AD是底边BC上的高,下面结论不一定成立的是 ( )
A.BD=CD B.BD=AD
C.AD平分∠BAC D.∠B=∠C
2.(冀教八上P143习题A组第1题(1)变式)如图,图中共有等腰三角形 ( )
A.4个 B.5个 C.3个 D.2个
3.已知等边△ABC的边长AB=8,则△ABC的面积为 ( )
A.16 B.24 C.32 D.64
4.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,D为AB的中点,则CD为 .
真题精粹·重变式——河北6年真题精选及拓展
考向1等腰三角形的性质与判定 (6年5考)
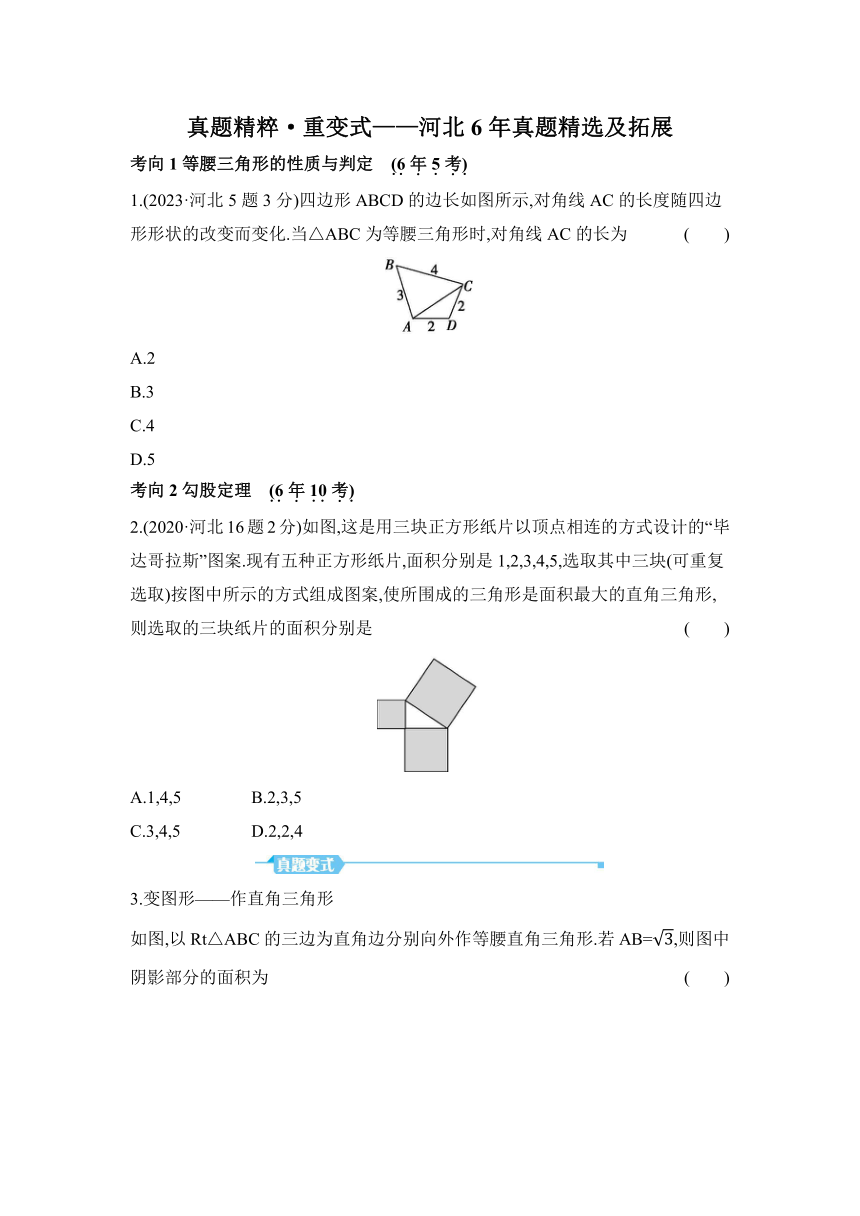
1.(2023·河北5题3分)四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时,对角线AC的长为 ( )
A.2
B.3
C.4
D.5
考向2勾股定理 (6年10考)
2.(2020·河北16题2分)如图,这是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图中所示的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.1,4,5 B.2,3,5
C.3,4,5 D.2,2,4
3.变图形——作直角三角形 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为 ( ) A.3 B. C.3 D.3
4.(2019·河北19题4分)勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据(单位:km)如图所示.笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 km.
核心突破·拓思维——学科核心素养提升
题型1 等腰三角形的性质与判定
(2024·邯郸二模)如图,M,N是∠AOB的边OA上的两个点(OM8;乙答:a=4.下列说法正确的是 ( )
A.只有甲对 B.只有乙对
C.甲、乙答案合一起才完整 D.甲、乙答案合一起也不对
等腰三角形以及特殊的等腰三角形——等边三角形,经常出现在河北省中考试卷的各种题型中,作为重要的构图要素,结合其他几何图形进行考查.在解题时,符合题意的图形如果有多种情况,一定要分类讨论,不能遗漏.
1.(2024·石家庄一模)对于题目:“在△ABC中,AB=AC,∠ABC=70°,分别以点A,B为圆心,AB的长为半径画弧,两条弧相交于点P,求∠APC的度数”.嘉嘉求解的结果是∠APC=80°,淇淇说:“嘉嘉的解答正确但不全面,∠APC还有另一个不同的值.”则下列判断中,正确的是 ( )
A.淇淇说得对,∠APC的另一个值是40°
B.淇淇说得不对,∠APC只能等于80°
C.嘉嘉求的结果不对,∠APC应等于85°
D.两人都不对,∠APC应有3个不同的值
2.有一题目:“如图,∠ABC=40°,BD平分∠ABC,过点D作DE∥AB交BC于点E,若点F在AB上,且满足DF=DE,求∠DFB的度数.”小贤的解答:以D为圆心,DE的长为半径画圆交AB于点F,连接DF,则DE=DF,由图形的对称性可得∠DFB=∠DEB.结合平行线的性质可求得∠DFB=140°.而小军说:“小贤考虑得不周全,∠DFB还应有另一个不同的值.”下列判断正确的是 ( )
A.小军说得对,且∠DFB的另一个值是40°
B.小军说得不对,∠DFB只能等于140°
C.小贤求的结果不对,∠DFB应该是20°
D.两人都不对,∠DFB应有3个不同的值
题型2 勾股定理
发现:如果两个连续的正整数的和可以表示成某一个正整数的平方,那么以这三个正整数为边长的三角形是直角三角形.
验证:如12+13=25=52,请判断以12,13和5为边长的三角形是否为直角三角形.
探究:设两个连续的正整数m和m+1的和可以表示成正整数n2,请论证“发现”中的结论正确.
求出∠BAC的度数
↓
依题意画出图形,两弧相交于点P,P',连接PB,P'B
↓
根据作图可知△APB,△AP'B均为等边三角形
↓
根据等腰三角形性质与三角形的内角和分别求出∠APC与∠AP'C的度数
↓
判断两人说法是否正确
小贤解答的可取之处在于通过构造辅助圆来确定点F的位置,但辅助圆与AB有两个交点,它们都符合条件,所以要分类讨论.在得到一种情况后,解答另外一种情况时,经常转化为第一种情况,或者利用第一种情况的结果.
勾股定理是关于直角三角形的著名定理,其中承载着中华优秀传统文化,是中考试卷的必考内容,既可以单独考查,也可以在几何综合题中作为重要工具使用,还能利用其数形结合的特点,与整式等代数知识相结合.
应用:寻找一组含正整数9,且满足“发现”中的结论的数字.
勾股定理使用策略
直角三角形
勾股定理↓↑逆定理
两条较小边的平方和等于最大边的平方
变↓式
最大边与另一边的平方差等于第三边的平方
1.如图,在4×4的正方形网格中,O为格点,点A,B都在网格线上,已知线段OA和线段OB的长都是整数,则= .
2.如图1,将长为3a+1、宽为2a的矩形分割成四个全等的直角三角形,再拼成“赵爽弦图”(如图2),得到两个正方形.
(1)图2中小正方形的边长为 (用含a的代数式表示).
(2)当a=1时,该大正方形的面积是 .
正方形(或长方形)网格中的网格线纵横交错形成直角,可以形成多个直角三角形,为利用勾股定理解题奠定了基础,所以,在网格图中求线段的长度,通常要借助网格线构造直角三角形,再利用勾股定理求解.熟记常见的勾股数能提高解题效率.
参考答案
考点清单
①底角 ②一 ③60° ④等腰 ⑤一半
⑥a2+b2=c2 ⑦30° ⑧余角
基础演练
1.B 2.B 3.A
4.4
真题精粹·重变式
1.B 2.B 3.A
4.(1)20 (2)13
核心突破·拓思维
例1 C
提示:如图,作线段MN的垂直平分线交OB于点P,连接PM,PN.
则PM=PN,此时△PMN是等腰三角形.
①过点M作MH⊥OB于点H,
当MH>MN,满足条件的点P恰好只有一个.
∵MN=4,∠AOB=30°,
当MH=4时,OM=2MH=8,
∴当a>8时,满足条件的点P恰好只有一个;
②当△PMN是等边三角形时,满足条件的点P恰好只有一个,
此时MN=MP,∠NMP=60°.
∵∠AOB=30°,∴∠MPO=30°,
∴OM=MP=MN=4,∴a=4.
综上所述,a的取值范围是a=4或a>8,故选C.
变式训练
1.A 提示:∵在△ABC中,AB=AC,∠ABC=70°,
∴∠ACB=∠ABC=70°,
∴∠BAC=180°-(∠ACB+∠ABC)=180°-(70°+70°)=40°,依题意分别以点A,B为圆心,AB的长为半径画弧,两条弧相交于点P,P',连接PB,P'B,如图所示,
根据作图可知:AB=AP=BP=AC=AP'=BP',
∴△APB,△AP'B均为等边三角形,
∴∠BAP=60°,∠BAP'=60°.
在△ACP中,AC=AP,∠CAP=∠BAP-∠BAC=20°,
∴∠APC=(180°-∠CAP)=(180°-20°)=80°.
在△AP'C中,AP'=AC,∠CAP'=∠BAP'+∠BAC=100°,
∴∠AP'C=(180°-∠CAP')=×(180°-100°)=40°,
∴淇淇说得对,∠APC的另一个值是40°.故选A.
2.A 提示:如图,以D为圆心,DE的长为半径画圆交AB于点F,F',连接DF,DF',则DE=DF=DF',∴∠DFF'=∠DF'F.
∵BD平分∠ABC,由图形的对称性可知∠DFB=∠DEB.
∵DE∥AB,∠ABC=40°,
∴∠DEB=180°-40°=140°,∴∠DFB=140°.
当点F位于点F'处时,
∵DF=DF',∴∠DF'B=∠DFF'=40°,故选A.
例2
验证:
52+122=169,132=169,
∴52+122=132,
∴以12,13和5为边长的三角形是直角三角形.
探究:
由“发现”得m+m+1=n2,
∴n2=2m+1,
∴n2+m2=m2+2m+1=(m+1)2,
∴以n,m,m+1为边长的三角形是直角三角形,
∴“发现”中的结论正确.
应用:
∵40+41=92,
∴92+402=1681,412=1681,
∴92+402=412,
∴以9,40,41为边长的三角形是直角三角形.
变式训练
1.5 提示:如图,由题意可得OD=2,OE=2,2由勾股定理,得OA2=OD2+AD2=4+AD2,
OB2=OE2+BE2=4+BE2,
∴8∵线段OA、线段OB的长都是整数,
∴OA2=9,OB2=16,
∴==5.
2.(1)2a+1 (2)17
提示:(1)∵直角三角形较短的直角边=×2a=a,
较长的直角边=3a+1,
∴小正方形的边长=3a+1-a=2a+1.
(2)由(1)得,当a=1时,直角三角形两条直角边的长分别为1,4,
∴大正方形的面积=()2=17.
(6年15考,2~7分)
等腰三角形和直角三角形主要考查等腰、等边和直角三角形的性质与判定,常见辅助线的作法以及分类讨论思想的应用.从难易度上分为两类,第一类以简单的计算或证明为主,第二类以等腰三角形或直角三角形为图形背景考查几何证明与计算.河北省中考一般作为背景考查,预计2025年仍将延续.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1等腰三角形的性质与判定 (常考点)
性质 1.等边对等角:两腰相等,两① 相等. 2.“三线合一”:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. 3.对称性:等腰三角形是轴对称图形,有② 条对称轴
判定 1.有两边相等的三角形是等腰三角形. 2.有两角相等的三角形是等腰三角形(等角对等边)
考点2等边三角形的性质与判定
性质1.边角关系:三边相等,三个内角相等且都等于③ . 2.“三线合一”:任意一边上的高、中线及其对角的平分线互相重合. 3.对称性:等边三角形是轴对称图形,三条高(或角平分线或中线)所在的直线是对称轴
判定1.定义:三边都相等的三角形是等边三角形. 2.三个角都相等(均为60°)的三角形是等边三角形. 3.有一个角为60°的④ 三角形是等边三角形
考点3直角三角形的性质与判定 (常考点)
性质1.两锐角互余. 2.30°角所对的直角边等于斜边的一半. 3.斜边上的中线等于斜边的⑤ . 4.勾股定理:两直角边a,b的平方和等于斜边c的平方,即⑥ . 5.在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于⑦
判定1.有一个角为90°的三角形是直角三角形. 2.两个锐角互为⑧ 的三角形是直角三角形. 3.勾股定理逆定理:已知三角形的边长分别为a,b,c,若a2+b2=c2,则这个三角形是直角三角形
【基础演练】
1.(人教八上P77第2题变式)如图,△ABC是等腰三角形,AB=AC,AD是底边BC上的高,下面结论不一定成立的是 ( )
A.BD=CD B.BD=AD
C.AD平分∠BAC D.∠B=∠C
2.(冀教八上P143习题A组第1题(1)变式)如图,图中共有等腰三角形 ( )
A.4个 B.5个 C.3个 D.2个
3.已知等边△ABC的边长AB=8,则△ABC的面积为 ( )
A.16 B.24 C.32 D.64
4.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,D为AB的中点,则CD为 .
真题精粹·重变式——河北6年真题精选及拓展
考向1等腰三角形的性质与判定 (6年5考)
1.(2023·河北5题3分)四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时,对角线AC的长为 ( )
A.2
B.3
C.4
D.5
考向2勾股定理 (6年10考)
2.(2020·河北16题2分)如图,这是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图中所示的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.1,4,5 B.2,3,5
C.3,4,5 D.2,2,4
3.变图形——作直角三角形 如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为 ( ) A.3 B. C.3 D.3
4.(2019·河北19题4分)勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据(单位:km)如图所示.笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 km.
核心突破·拓思维——学科核心素养提升
题型1 等腰三角形的性质与判定
(2024·邯郸二模)如图,M,N是∠AOB的边OA上的两个点(OM
A.只有甲对 B.只有乙对
C.甲、乙答案合一起才完整 D.甲、乙答案合一起也不对
等腰三角形以及特殊的等腰三角形——等边三角形,经常出现在河北省中考试卷的各种题型中,作为重要的构图要素,结合其他几何图形进行考查.在解题时,符合题意的图形如果有多种情况,一定要分类讨论,不能遗漏.
1.(2024·石家庄一模)对于题目:“在△ABC中,AB=AC,∠ABC=70°,分别以点A,B为圆心,AB的长为半径画弧,两条弧相交于点P,求∠APC的度数”.嘉嘉求解的结果是∠APC=80°,淇淇说:“嘉嘉的解答正确但不全面,∠APC还有另一个不同的值.”则下列判断中,正确的是 ( )
A.淇淇说得对,∠APC的另一个值是40°
B.淇淇说得不对,∠APC只能等于80°
C.嘉嘉求的结果不对,∠APC应等于85°
D.两人都不对,∠APC应有3个不同的值
2.有一题目:“如图,∠ABC=40°,BD平分∠ABC,过点D作DE∥AB交BC于点E,若点F在AB上,且满足DF=DE,求∠DFB的度数.”小贤的解答:以D为圆心,DE的长为半径画圆交AB于点F,连接DF,则DE=DF,由图形的对称性可得∠DFB=∠DEB.结合平行线的性质可求得∠DFB=140°.而小军说:“小贤考虑得不周全,∠DFB还应有另一个不同的值.”下列判断正确的是 ( )
A.小军说得对,且∠DFB的另一个值是40°
B.小军说得不对,∠DFB只能等于140°
C.小贤求的结果不对,∠DFB应该是20°
D.两人都不对,∠DFB应有3个不同的值
题型2 勾股定理
发现:如果两个连续的正整数的和可以表示成某一个正整数的平方,那么以这三个正整数为边长的三角形是直角三角形.
验证:如12+13=25=52,请判断以12,13和5为边长的三角形是否为直角三角形.
探究:设两个连续的正整数m和m+1的和可以表示成正整数n2,请论证“发现”中的结论正确.
求出∠BAC的度数
↓
依题意画出图形,两弧相交于点P,P',连接PB,P'B
↓
根据作图可知△APB,△AP'B均为等边三角形
↓
根据等腰三角形性质与三角形的内角和分别求出∠APC与∠AP'C的度数
↓
判断两人说法是否正确
小贤解答的可取之处在于通过构造辅助圆来确定点F的位置,但辅助圆与AB有两个交点,它们都符合条件,所以要分类讨论.在得到一种情况后,解答另外一种情况时,经常转化为第一种情况,或者利用第一种情况的结果.
勾股定理是关于直角三角形的著名定理,其中承载着中华优秀传统文化,是中考试卷的必考内容,既可以单独考查,也可以在几何综合题中作为重要工具使用,还能利用其数形结合的特点,与整式等代数知识相结合.
应用:寻找一组含正整数9,且满足“发现”中的结论的数字.
勾股定理使用策略
直角三角形
勾股定理↓↑逆定理
两条较小边的平方和等于最大边的平方
变↓式
最大边与另一边的平方差等于第三边的平方
1.如图,在4×4的正方形网格中,O为格点,点A,B都在网格线上,已知线段OA和线段OB的长都是整数,则= .
2.如图1,将长为3a+1、宽为2a的矩形分割成四个全等的直角三角形,再拼成“赵爽弦图”(如图2),得到两个正方形.
(1)图2中小正方形的边长为 (用含a的代数式表示).
(2)当a=1时,该大正方形的面积是 .
正方形(或长方形)网格中的网格线纵横交错形成直角,可以形成多个直角三角形,为利用勾股定理解题奠定了基础,所以,在网格图中求线段的长度,通常要借助网格线构造直角三角形,再利用勾股定理求解.熟记常见的勾股数能提高解题效率.
参考答案
考点清单
①底角 ②一 ③60° ④等腰 ⑤一半
⑥a2+b2=c2 ⑦30° ⑧余角
基础演练
1.B 2.B 3.A
4.4
真题精粹·重变式
1.B 2.B 3.A
4.(1)20 (2)13
核心突破·拓思维
例1 C
提示:如图,作线段MN的垂直平分线交OB于点P,连接PM,PN.
则PM=PN,此时△PMN是等腰三角形.
①过点M作MH⊥OB于点H,
当MH>MN,满足条件的点P恰好只有一个.
∵MN=4,∠AOB=30°,
当MH=4时,OM=2MH=8,
∴当a>8时,满足条件的点P恰好只有一个;
②当△PMN是等边三角形时,满足条件的点P恰好只有一个,
此时MN=MP,∠NMP=60°.
∵∠AOB=30°,∴∠MPO=30°,
∴OM=MP=MN=4,∴a=4.
综上所述,a的取值范围是a=4或a>8,故选C.
变式训练
1.A 提示:∵在△ABC中,AB=AC,∠ABC=70°,
∴∠ACB=∠ABC=70°,
∴∠BAC=180°-(∠ACB+∠ABC)=180°-(70°+70°)=40°,依题意分别以点A,B为圆心,AB的长为半径画弧,两条弧相交于点P,P',连接PB,P'B,如图所示,
根据作图可知:AB=AP=BP=AC=AP'=BP',
∴△APB,△AP'B均为等边三角形,
∴∠BAP=60°,∠BAP'=60°.
在△ACP中,AC=AP,∠CAP=∠BAP-∠BAC=20°,
∴∠APC=(180°-∠CAP)=(180°-20°)=80°.
在△AP'C中,AP'=AC,∠CAP'=∠BAP'+∠BAC=100°,
∴∠AP'C=(180°-∠CAP')=×(180°-100°)=40°,
∴淇淇说得对,∠APC的另一个值是40°.故选A.
2.A 提示:如图,以D为圆心,DE的长为半径画圆交AB于点F,F',连接DF,DF',则DE=DF=DF',∴∠DFF'=∠DF'F.
∵BD平分∠ABC,由图形的对称性可知∠DFB=∠DEB.
∵DE∥AB,∠ABC=40°,
∴∠DEB=180°-40°=140°,∴∠DFB=140°.
当点F位于点F'处时,
∵DF=DF',∴∠DF'B=∠DFF'=40°,故选A.
例2
验证:
52+122=169,132=169,
∴52+122=132,
∴以12,13和5为边长的三角形是直角三角形.
探究:
由“发现”得m+m+1=n2,
∴n2=2m+1,
∴n2+m2=m2+2m+1=(m+1)2,
∴以n,m,m+1为边长的三角形是直角三角形,
∴“发现”中的结论正确.
应用:
∵40+41=92,
∴92+402=1681,412=1681,
∴92+402=412,
∴以9,40,41为边长的三角形是直角三角形.
变式训练
1.5 提示:如图,由题意可得OD=2,OE=2,2
OB2=OE2+BE2=4+BE2,
∴8
∴OA2=9,OB2=16,
∴==5.
2.(1)2a+1 (2)17
提示:(1)∵直角三角形较短的直角边=×2a=a,
较长的直角边=3a+1,
∴小正方形的边长=3a+1-a=2a+1.
(2)由(1)得,当a=1时,直角三角形两条直角边的长分别为1,4,
∴大正方形的面积=()2=17.
同课章节目录
