【中考考点探究】第3节 两个三角形的关系 第2讲 相似三角形(含位似) 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第3节 两个三角形的关系 第2讲 相似三角形(含位似) 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:37:19 | ||
图片预览



文档简介
第2讲 相似三角形(含位似)
(6年8考,1~12分)
图形的相似主要考查相似三角形的性质与判定,从难易程度上来说,一类以简单相似图形的识别或计算为主,一类以在具体情境中考查相似三角形的证明与应用为主.河北中考图形的相似有时单独考查,有时与其他知识结合,预测2025年河北省中考试题仍将延续这一命题特点,并会在压轴题中考查A字型、8字型、一线三等角等典型的相似图形.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1比例线段的相关概念及性质
比例线段 在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即=,那么这四条线段a,b,c,d叫作成比例线段,简称比例线段
比例的基本性质 1.基本性质:= ad=① (b,d≠0). 2.合比性质:= =(b,d≠0). 3.分比性质:= =② .(b,d≠0) 4.等比性质:如果==…==k(b+d+…+n≠0),那么=③ . 【温馨提示】更比定理:= =
黄金分割 如图,点C把线段AB分成两条线段AC和BC,如果==≈0.618,那么这个比值叫作黄金比,线段AB被点C黄金分割.其中C叫作线段AB的黄金分割点
考点2平行线分线段成比例 (轮考点)
基本事实 两条直线被一组平行线所截,所得的对应线段④ .如图,两条直线 l1和l2被三条互相平行的直线AD,BE,CF所截,则=,=, =
推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.如图1和图2,若DE∥BC,则=或=⑤ 或=⑥ ,图1也可以说=或=或⑦ =
考点3相似三角形的判定与性质 (常考点)
相似三角形的判定1.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似; 2.三边对应成比例的两个三角形⑧ ; 3.两边对应成比例且⑨ 相等的两个三角形相似; 4.两角对应相等的两个三角形相似
相似三角形的性质1.对应角相等,对应边成比例; 2.周长之比等于⑩ ,面积之比等于 ; 3.相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比
考点4图形的位似
概念如果两个图形不仅是相似图形,而且对应点的连线相交于一点,对应线段相互平行(或在一条直线上),像这样的两个图形叫作位似图形,这个交点叫作位似中心,这时的相似比又称为位似比
位似图形的性质1.位似图形是相似图形,具备相似图形的所有性质; 2.对应点的连线经过同一点; 3.位似图形上的任意一对对应点到位似中心的距离之比等于相似比; 4.位似图形中的对应线段平行(或在同一条直线上)
【基础演练】
1.(北师九上P79随堂练习第2题变式)若3a=4b(b≠0),则的值为 ( )
A. B.
C. D.
2.(北师九上P84第1题(1)变式)如图,已知AB∥CD∥EF,BD∶DF=1∶2,那么下列结论中,正确的是 ( )
A.AC∶AE=1∶3
B.CE∶EA=1∶3
C.CD∶EF=1∶2
D.AB∶EF=1∶2
3.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO∶OE=2∶1,则△ABC与△DEF的面积之比是 ( )
A.1∶2
B.1∶4
C.2∶1
D.4∶1
4.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC=∠ADB,AD=2,AC=6,则AB的长为 ( )
A.3
B.4
C.
D.2
真题精粹·重变式——河北6年真题精选及拓展
考向1相似三角形的判定与性质 (6年8考)
1.(2021·河北8题3分)图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB的长度为 ( )
A.1 cm B.2 cm C.3 cm D.4 cm
2.(2022·河北18题3分)如图,这是钉板示意图,每相邻4个钉点是边长为1个单位长度的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E,则
(1)AB与CD是否垂直 (填“是”或“否”).
(2)AE= .
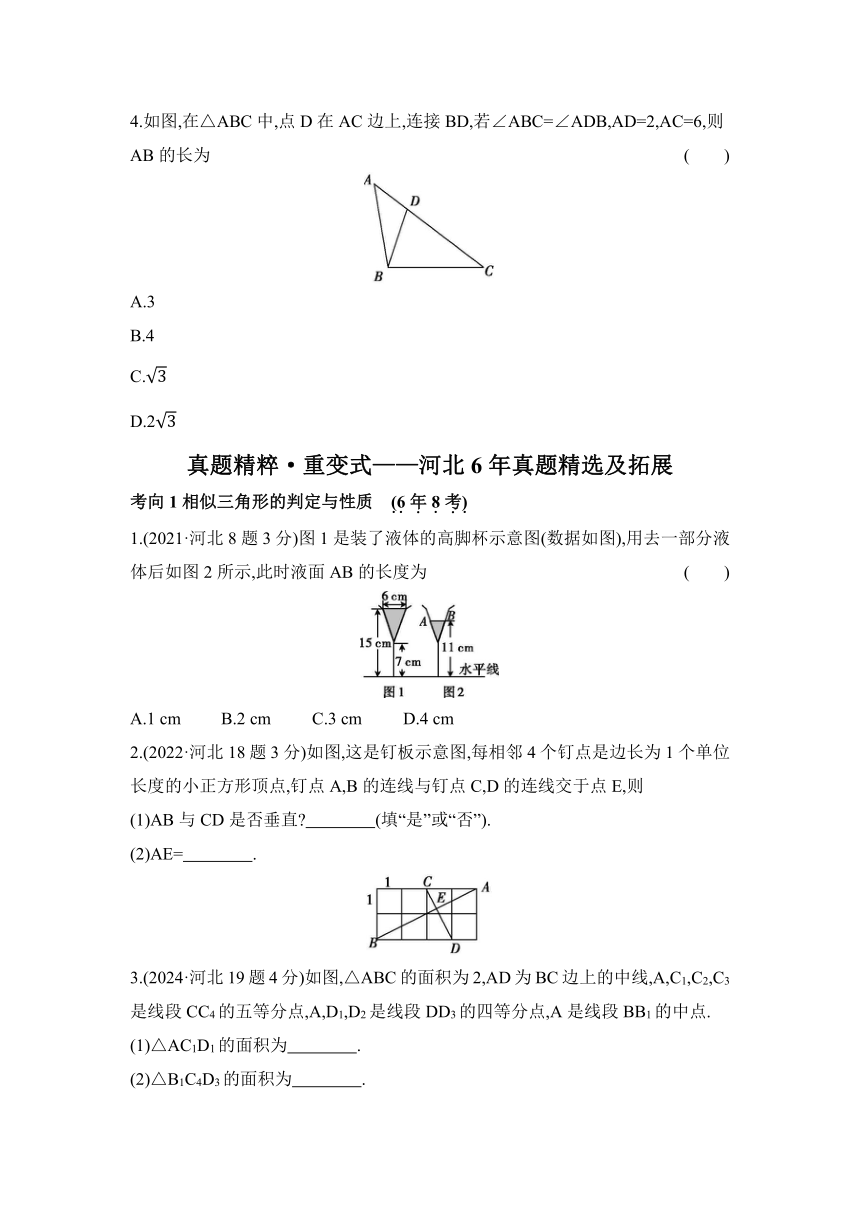
3.(2024·河北19题4分)如图,△ABC的面积为2,AD为BC边上的中线,A,C1,C2,C3是线段CC4的五等分点,A,D1,D2是线段DD3的四等分点,A是线段BB1的中点.
(1)△AC1D1的面积为 .
(2)△B1C4D3的面积为 .
考向2位似 (6年3考)
4.(2020·河北8题3分)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是 ( )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
核心突破·拓思维——学科核心素养提升
题型 相似三角形的判定与性质
如图,在等边△ABC中,直尺(单位:cm)的一边与BC重合,另一边分别交AB,AC于点D,E,点B,C,D,E处的读数分别为18,14,1,3.
(1)等边△ABC的边长为 cm.
(2)直尺的宽为 cm.
(1)观察图中数据,可以得到BC的长度,即等边△ABC的边长.
(2)作△ABC中BC边上的高,依据“相似三角形的高的比等于相似比”,列比例式求解.
(原创·一图多变)在△ABC中,D,E分别是AB,AC边上的点.
(1)如图1,当DE∥BC时:
①请写出图中的相似三角形: ;
②若=,DE=6,则BC= ;
③连接DC,BE交于点O,若D为AB的中点,四边形DECB的面积等于9,则△ADE的面积为 ,△DOE的面积为 .
(2)如图2,当DE与BC不平行时:
①请添加一个条件 (写一个即可),使得△ADE∽△ACB;
②若△ADE∽△ACB,且=,DE=10,则BC= .
(3)如图3,当点E与点C重合时,若∠ADC=∠ACB, AD=3,BD=2,则△ACD与△ABC的相似比为 .
(4)如图4,当∠C=90°,且ED⊥AB 时:
①写出图中的相似三角形: .
②如图5,点E与点C重合,写出图中的相似三角形: ; 若AD=9,BD=4,则CD= ,AC= .
相似三角形的常见图形之间存在着密切关系.我们还可以将DE向上平移与AB,AC的反向延长线相交,得到如下图形.若带有标记的两个角相等,则图中的两个三角形仍然相似.
参考答案
考点清单
①bc ② ③k ④成比例 ⑤ ⑥ ⑦
⑧相似 ⑨夹角 ⑩相似比 相似比的平方
基础演练
1.C 2.A 3.D 4.D
真题精粹·重变式
1.C
2.(1)是 (2)
3.(1)1 (2)7
提示:(1)如图,连接B1D1,B1D2,B1C2,B1C3,C3D3.
∵△ABC的面积为2,AD为BC边上的中线,
∴S△ABD=S△ACD=S△ABC=×2=1.
∵A,C1,C2,C3是线段CC4的五等分点,
∴AC=AC1=C1C2=C2C3=C3C4=CC4.
∵A,D1,D2是线段DD3的四等分点,
∴AD=AD1=D1D2=D2D3=DD3.
∵A是线段BB1的中点,
∴AB=AB1=BB1.
在△AC1D1和△ACD中,
∴△AC1D1≌△ACD(SAS),
∴=S△ACD=1,∠C1D1A=∠CDA,
∴△AC1D1的面积为1,
故答案为1.
(2)在△AB1D1和△ABD中,
∴△AB1D1≌△ABD(SAS),
∴=S△ABD=1,∠B1D1A=∠BDA.
∵∠BDA+∠CDA=180°,
∴∠B1D1A+∠C1D1A=180°,
∴C1,D1,B1三点共线,
∴=+=1+1=2.
∵AC1=C1C2=C2C3=C3C4,
∴=4=4×2=8.
∵AD1=D1D2=D2D3,=1,
∴=3=3×1=3.
在△C3AD3和△CAD中,
=3=,∠C3AD3=∠CAD,
∴△C3AD3∽△CAD,
∴=2=32=9,
∴=9S△CAD=9×1=9.
∵AC1=C1C2=C2C3=C3C4,
∴==×9=12,
∴=+-=12+3-8=7,
∴△B1C4D3的面积为7,
故答案为7.
4.A
核心突破·拓思维
例1(1)4 (2)
提示:(1)由题意,得BC=18-14=4(cm).
∵△ABC是等边三角形,∴AB=AC=BC=4(cm),
∴等边△ABC的边长为4 cm.
(2)如图,过点A作AF⊥DE,垂足为F,延长AF交BC于点G.
∵△ABC是等边三角形,DE∥BC,
∴AG⊥BC,∴BG=BC=2(cm).
∵AB=4 cm,∴AG===2(cm).
由题意得DE=3-1=2(cm),DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,∴=,∴=,
∴AF= cm,∴FG=AG-AF=(cm),∴直尺的宽为 cm.
变式训练
(1)①△ADE∽△ABC ②15 ③3 1
(2)①∠ADE=∠ACB或∠AED=∠ABC或AD∶AC=AE∶AB ②15
(3)
(4)①△ADE∽△ACB ②△ADC∽△ACB∽△CDB
6 3
(6年8考,1~12分)
图形的相似主要考查相似三角形的性质与判定,从难易程度上来说,一类以简单相似图形的识别或计算为主,一类以在具体情境中考查相似三角形的证明与应用为主.河北中考图形的相似有时单独考查,有时与其他知识结合,预测2025年河北省中考试题仍将延续这一命题特点,并会在压轴题中考查A字型、8字型、一线三等角等典型的相似图形.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1比例线段的相关概念及性质
比例线段 在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即=,那么这四条线段a,b,c,d叫作成比例线段,简称比例线段
比例的基本性质 1.基本性质:= ad=① (b,d≠0). 2.合比性质:= =(b,d≠0). 3.分比性质:= =② .(b,d≠0) 4.等比性质:如果==…==k(b+d+…+n≠0),那么=③ . 【温馨提示】更比定理:= =
黄金分割 如图,点C把线段AB分成两条线段AC和BC,如果==≈0.618,那么这个比值叫作黄金比,线段AB被点C黄金分割.其中C叫作线段AB的黄金分割点
考点2平行线分线段成比例 (轮考点)
基本事实 两条直线被一组平行线所截,所得的对应线段④ .如图,两条直线 l1和l2被三条互相平行的直线AD,BE,CF所截,则=,=, =
推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.如图1和图2,若DE∥BC,则=或=⑤ 或=⑥ ,图1也可以说=或=或⑦ =
考点3相似三角形的判定与性质 (常考点)
相似三角形的判定1.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似; 2.三边对应成比例的两个三角形⑧ ; 3.两边对应成比例且⑨ 相等的两个三角形相似; 4.两角对应相等的两个三角形相似
相似三角形的性质1.对应角相等,对应边成比例; 2.周长之比等于⑩ ,面积之比等于 ; 3.相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比
考点4图形的位似
概念如果两个图形不仅是相似图形,而且对应点的连线相交于一点,对应线段相互平行(或在一条直线上),像这样的两个图形叫作位似图形,这个交点叫作位似中心,这时的相似比又称为位似比
位似图形的性质1.位似图形是相似图形,具备相似图形的所有性质; 2.对应点的连线经过同一点; 3.位似图形上的任意一对对应点到位似中心的距离之比等于相似比; 4.位似图形中的对应线段平行(或在同一条直线上)
【基础演练】
1.(北师九上P79随堂练习第2题变式)若3a=4b(b≠0),则的值为 ( )
A. B.
C. D.
2.(北师九上P84第1题(1)变式)如图,已知AB∥CD∥EF,BD∶DF=1∶2,那么下列结论中,正确的是 ( )
A.AC∶AE=1∶3
B.CE∶EA=1∶3
C.CD∶EF=1∶2
D.AB∶EF=1∶2
3.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO∶OE=2∶1,则△ABC与△DEF的面积之比是 ( )
A.1∶2
B.1∶4
C.2∶1
D.4∶1
4.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC=∠ADB,AD=2,AC=6,则AB的长为 ( )
A.3
B.4
C.
D.2
真题精粹·重变式——河北6年真题精选及拓展
考向1相似三角形的判定与性质 (6年8考)
1.(2021·河北8题3分)图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB的长度为 ( )
A.1 cm B.2 cm C.3 cm D.4 cm
2.(2022·河北18题3分)如图,这是钉板示意图,每相邻4个钉点是边长为1个单位长度的小正方形顶点,钉点A,B的连线与钉点C,D的连线交于点E,则
(1)AB与CD是否垂直 (填“是”或“否”).
(2)AE= .
3.(2024·河北19题4分)如图,△ABC的面积为2,AD为BC边上的中线,A,C1,C2,C3是线段CC4的五等分点,A,D1,D2是线段DD3的四等分点,A是线段BB1的中点.
(1)△AC1D1的面积为 .
(2)△B1C4D3的面积为 .
考向2位似 (6年3考)
4.(2020·河北8题3分)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是 ( )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
核心突破·拓思维——学科核心素养提升
题型 相似三角形的判定与性质
如图,在等边△ABC中,直尺(单位:cm)的一边与BC重合,另一边分别交AB,AC于点D,E,点B,C,D,E处的读数分别为18,14,1,3.
(1)等边△ABC的边长为 cm.
(2)直尺的宽为 cm.
(1)观察图中数据,可以得到BC的长度,即等边△ABC的边长.
(2)作△ABC中BC边上的高,依据“相似三角形的高的比等于相似比”,列比例式求解.
(原创·一图多变)在△ABC中,D,E分别是AB,AC边上的点.
(1)如图1,当DE∥BC时:
①请写出图中的相似三角形: ;
②若=,DE=6,则BC= ;
③连接DC,BE交于点O,若D为AB的中点,四边形DECB的面积等于9,则△ADE的面积为 ,△DOE的面积为 .
(2)如图2,当DE与BC不平行时:
①请添加一个条件 (写一个即可),使得△ADE∽△ACB;
②若△ADE∽△ACB,且=,DE=10,则BC= .
(3)如图3,当点E与点C重合时,若∠ADC=∠ACB, AD=3,BD=2,则△ACD与△ABC的相似比为 .
(4)如图4,当∠C=90°,且ED⊥AB 时:
①写出图中的相似三角形: .
②如图5,点E与点C重合,写出图中的相似三角形: ; 若AD=9,BD=4,则CD= ,AC= .
相似三角形的常见图形之间存在着密切关系.我们还可以将DE向上平移与AB,AC的反向延长线相交,得到如下图形.若带有标记的两个角相等,则图中的两个三角形仍然相似.
参考答案
考点清单
①bc ② ③k ④成比例 ⑤ ⑥ ⑦
⑧相似 ⑨夹角 ⑩相似比 相似比的平方
基础演练
1.C 2.A 3.D 4.D
真题精粹·重变式
1.C
2.(1)是 (2)
3.(1)1 (2)7
提示:(1)如图,连接B1D1,B1D2,B1C2,B1C3,C3D3.
∵△ABC的面积为2,AD为BC边上的中线,
∴S△ABD=S△ACD=S△ABC=×2=1.
∵A,C1,C2,C3是线段CC4的五等分点,
∴AC=AC1=C1C2=C2C3=C3C4=CC4.
∵A,D1,D2是线段DD3的四等分点,
∴AD=AD1=D1D2=D2D3=DD3.
∵A是线段BB1的中点,
∴AB=AB1=BB1.
在△AC1D1和△ACD中,
∴△AC1D1≌△ACD(SAS),
∴=S△ACD=1,∠C1D1A=∠CDA,
∴△AC1D1的面积为1,
故答案为1.
(2)在△AB1D1和△ABD中,
∴△AB1D1≌△ABD(SAS),
∴=S△ABD=1,∠B1D1A=∠BDA.
∵∠BDA+∠CDA=180°,
∴∠B1D1A+∠C1D1A=180°,
∴C1,D1,B1三点共线,
∴=+=1+1=2.
∵AC1=C1C2=C2C3=C3C4,
∴=4=4×2=8.
∵AD1=D1D2=D2D3,=1,
∴=3=3×1=3.
在△C3AD3和△CAD中,
=3=,∠C3AD3=∠CAD,
∴△C3AD3∽△CAD,
∴=2=32=9,
∴=9S△CAD=9×1=9.
∵AC1=C1C2=C2C3=C3C4,
∴==×9=12,
∴=+-=12+3-8=7,
∴△B1C4D3的面积为7,
故答案为7.
4.A
核心突破·拓思维
例1(1)4 (2)
提示:(1)由题意,得BC=18-14=4(cm).
∵△ABC是等边三角形,∴AB=AC=BC=4(cm),
∴等边△ABC的边长为4 cm.
(2)如图,过点A作AF⊥DE,垂足为F,延长AF交BC于点G.
∵△ABC是等边三角形,DE∥BC,
∴AG⊥BC,∴BG=BC=2(cm).
∵AB=4 cm,∴AG===2(cm).
由题意得DE=3-1=2(cm),DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,∴=,∴=,
∴AF= cm,∴FG=AG-AF=(cm),∴直尺的宽为 cm.
变式训练
(1)①△ADE∽△ABC ②15 ③3 1
(2)①∠ADE=∠ACB或∠AED=∠ABC或AD∶AC=AE∶AB ②15
(3)
(4)①△ADE∽△ACB ②△ADC∽△ACB∽△CDB
6 3
同课章节目录
