【中考考点探究】第2节 特殊的四边形 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第2节 特殊的四边形 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 345.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:42:04 | ||
图片预览




文档简介
第2节 特殊的四边形
(6年7考,2~3分)
在最近三年的中考选择题中,以图中标注数据、判断画图方案、补充证明过程等不同方式考查平行四边形的判定.特殊四边形主要考查矩形、菱形、正方形的性质,涉及图形的剪裁、拼接等.一般在选择题和填空题中出现,考查基本性质与判定,也在探究题中作为铺垫性内容,考查将复杂图形转化为基本图形解决问题的能力.河北省近5年都在选择题中出现,预测2025年河北省中考仍将延续这一命题特点.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点特殊四边形的性质与判定 (常考点)
特殊四边形 平行四边形 矩形 菱形 正方形
图形
性质 1.对边① . 2.两组对角分别相等. 3.对角线互相平分. 4.中心对称图形. 5.周长C=2(a+b),面积S=ah 1.对边平行且相等. 2.四个角都是② . 3.对角线互相平分且相等. 4.既是中心对称图形,也是轴对称图形,有2条对称轴. 5.周长C=2(a+b),面积S=ab 1.四条边③ . 2.两组对角分别相等. 3.对角线互相④ ,且平分⑤ . 4.既是中心对称图形,也是轴对称图形,有2条对称轴. 5.周长C=4a,面积S=ah=mn 1.四条边相等. 2.四个角都是直角. 3.对角线互相垂直平分且相等,平分一组对角. 4.既是中心对称图形,也是轴对称图形,有4条对称轴. 5.周长C=4a, 面积S=a2=m2
判定 1.定义法:两组对边分别平行的四边形. 2.两组对边分别相等的四边形. 3.一组对边⑥ 的四边形. 4.两组对角分别相等的四边形. 5.两条对角线互相平分的四边形 1.定义法:有一个角是⑦ 的平行四边形. 2.有三个角是直角的四边形. 3.对角线⑧ 的平行四边形 1.定义法:有一组邻边⑨ 的平行四边形. 2.四条边都相等的四边形. 3.对角线互相⑩ 的平行四边形 1.定义法:有一个角是直角,且有一组邻边相等的平行四边形. 2.一组邻边相等的矩形. 3.有一个角是直角的菱形. 4.对角线相等且互相垂直、平分的四边形
【基础演练】
1.(北师九上P26第4题变式)已知菱形的两条对角线长分别是7和8,则菱形的面积是 ( )
A.56 B.28
C.15 D.20
2.(北师九上P13第2题变式)如图,在矩形ABCD中,对角线AC,BD相交于点O,若AB=2,∠AOB=60°,则AC的长为 ( )
A.2
B.3
C.4
D.6
3.如图,在平行四边形ABCD中,下列结论错误的是 ( )
A.AD∥BC
B.AB=DC
C.∠DAB=∠BCD
D.AC=BD
4.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED的度数为 ( )
A.15°
B.30°
C.45°
D.60°
5.(北师九上P29第20题改编)小琦在复习几种特殊四边形的关系时整理如图所示,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是 ( )
A.(1)处可填∠A=90°
B.(2)处可填AD=AB
C.(3)处可填DC=CB
D.(4)处可填∠B=∠D
真题精粹·重变式——河北6年真题精选及拓展
考向1特殊四边形的判定 (6年4考)
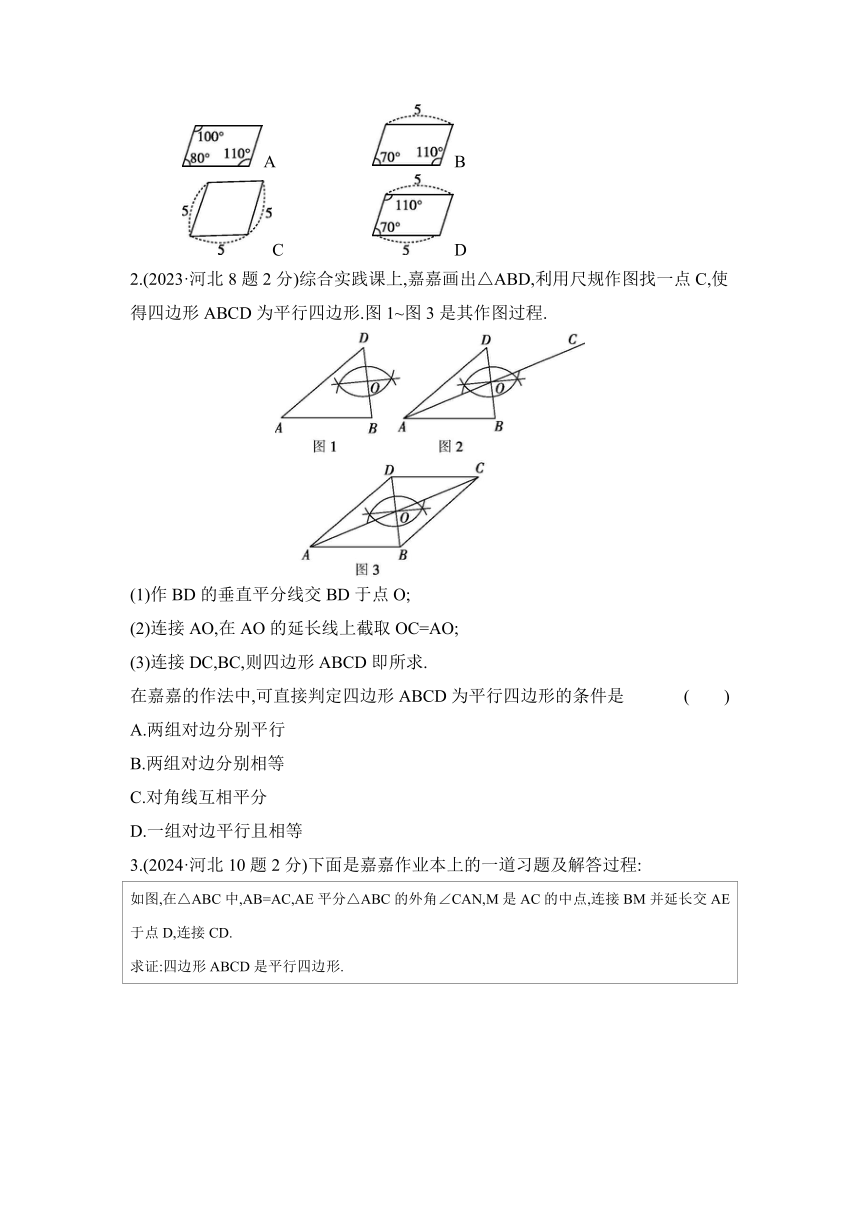
1.(2022·河北8题3分)依据所标数据,下列一定为平行四边形的是 ( )
A B
C D
2.(2023·河北8题2分)综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.图1~图3是其作图过程.
(1)作BD的垂直平分线交BD于点O;
(2)连接AO,在AO的延长线上截取OC=AO;
(3)连接DC,BC,则四边形ABCD即所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是 ( )
A.两组对边分别平行
B.两组对边分别相等
C.对角线互相平分
D.一组对边平行且相等
3.(2024·河北10题2分)下面是嘉嘉作业本上的一道习题及解答过程:
如图,在△ABC中,AB=AC,AE平分△ABC的外角∠CAN,M是AC的中点,连接BM并延长交AE于点D,连接CD. 求证:四边形ABCD是平行四边形. 证明:∵AB=AC, ∴∠ABC=∠3. ∵∠CAN=∠ABC+∠3,∠CAN=∠1+∠2,∠1=∠2, ∴① . 又∵∠4=∠5,MA=MC, ∴△MAD≌△MCB(② ), ∴MD=MB,∴四边形ABCD是平行四边形.
若以上解答过程正确,则①,②应分别为 ( )
A.∠1=∠3,AAS
B.∠1=∠3,ASA
C.∠2=∠3,AAS
D.∠2=∠3,ASA
4.(2020·河北10题3分)如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成了平行四边形,并推理如下:
点A,C分别转到了点C,A处, 而点B转到了点D处. ∵CB=AD, ∴四边形ABCD是平行四边形.
小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形……”之间作补充.下列选项中正确的是 ( )
A.嘉淇推理严谨,不必补充
B.应补充:且AB=CD
C.应补充:且AB∥CD
D.应补充:且OA=OC
考向2特殊四边形的性质 (6年3考)
5.(2019·河北5题3分)如图,在菱形ABCD中,∠D=150°,则∠1的度数为 ( )
A.30° B.25° C.20° D.15°
6.(2023·河北11题2分)如图,在Rt△ABC中,AB=4,M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC= ( )
A.4
B.8
C.12
D.16
核心突破·拓思维——学科核心素养提升
题型1 特殊四边形的三要素
(2024·邯郸二模)在 ABCD中,EF经过两条对角线的交点O,分别交AB,CD于点E,F,在对角线AC上通过作图得到点M,N,如图1,图2,下面关于以F,M,E,N为顶点的四边形的形状的说法正确的是 ( )
图1 以点O为圆心,OE的长为半径作弧,交AC于点M,N 图2 过点E作EM⊥AC于点M,过点F作FN⊥AC于点N
A.都为矩形
B.都为菱形
C.图1为矩形,图2为平行四边形
D.图1为矩形,图2为菱形
无论是特殊的平行四边形,还是一般的平行四边形,命题的着眼点都在于它们的边、角和对角线三个基本要素,这也是反映它们的定义、性质和判定方法的研究方向.在具体的题目中,三要素的考查各有侧重,信息的呈现方式灵活多样.可以在选择题中单独考查,也可以在解答题中作为重要的构图内容进行考查.除三要素外,它们的对称性、面积也时有考查.
1.斜边为2的两个全等的含30°的直角三角板,按照如图1所示的方式拼成一个矩形,将一个三角板保持不动,另一个三角板沿斜边向右下方向滑动,当四边形ABCD是菱形时,如图2,则平移距离AE的长为 ( )
A.1 B.
C. D.2
2.如图,正方形ABCD的边长为6,点E,F分别在DC,BC上,BF=CE,连接AE,DF,AE与DF相交于点G,连接AF,取AF的中点H,连接HG,若AE=2,则GH的长为 ( )
A. B.2
C.2 D.4
题型2 特殊四边形之间的联系与转化
(2024·石家庄一模)小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为如图1所示的菱形,并测得∠B=60°,接着活动学具成为如图2所示的正方形,并测得对角线AC=20,则图1中菱形的对角线BD的长为 ( )
A.20 B.30
C.20 D.20
只要证明EA=ED即可解决问题.
由正方形的性质结合勾股定理先后求出DE及CE的长,由BF=CE,根据勾股定理求AF的长,证明△ADE≌△DCF(SAS),得出∠DAE=∠CDF,求出∠AGF=∠DGE=90°,再由直角三角形的性质即可得出答案.
矩形、菱形、正方形之间,以及它们与平行四边形之间有着密切的关系,可以通过边、角、对角线的变化进行转化,特别是由一般到特殊的转化,体现了知识之间的内在联系.此类问题在中考试卷上,经常以动态操作的方式呈现,解题时要注意在操作过程中保持不变的数量关系或位置关系,以及动态变化过程中的特殊时刻.
特殊的四边形从属关系图
1.如图,在 ABCD中,∠ABC=α,BC>AB,E,F,G,H分别是AB,BC,CD,DA的中点,顺次连接E,F,G,H,在α从0°逐渐增大到180°的过程中,四边形EFGH形状的变化依次是 ( )
A.平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形
C.平行四边形→菱形→正方形→平行四边形
D.平行四边形→矩形→正方形→平行四边形
2.如图,已知△ABC和△DEF是两个边长都为10 cm的等边三角形,且点B,D,C,E都在一条直线上,连接AD,CF.
(1)四边形ADFC的形状是 .
(2)若BD=3 cm,此时△ABC沿着BE方向以1 cm/s的速度运动,运动时间为t.
①当四边形ADFC是菱形时,它的面积是 cm2;
②当运动时间t= s时,四边形ADFC是矩形.
(1)通过一组对边AC与DF平行且相等,判定四边形ADFC的形状.
(2)①根据菱形的性质可知此时点B与点D重合,则菱形的面积等于2个等边三角形的面积和;
②根据矩形的判定条件可知此时的对角线相等,则点B与点E重合,画图求解.
参考答案
考点清单
①平行且相等 ②直角 ③相等 ④平分且垂直
⑤一组对角 ⑥平行且相等 ⑦直角 ⑧相等
⑨相等 ⑩垂直
基础演练
1.B 2.C 3.D 4.C 5.D
真题精粹·重变式
1.D 2.C 3.D 4.B 5.D 6.B
核心突破·拓思维
例1 C
提示:在 ABCD中,AB∥DC,OA=OC,
∴∠FCO=∠EAO,∠CFO=∠AEO.
在△FCO和△EAO中,
∴△FCO≌△EAO(AAS),
∴OE=OF.
由图1作图可得OE=OF=OM=ON,
∴图1中以F,M,E,N为顶点的四边形为矩形.
由图2作图可得EM⊥AC,FN⊥AC,
∴∠EMO=∠FNO=90°.
在△OME和△ONF中,
∴△OME≌△ONF(AAS),
∴OM=ON.
又∵OE=OF,
∴图2中以F,M,E,N为顶点的四边形为平行四边形,故选C.
变式训练
1.A
2.A 提示:∵四边形ABCD为正方形,
∴AB=BC=CD=AD=6,∠B=∠C=∠ADE=90°,
∴DE===2,
∴BF=CE=CD-DE=6-2=4,
∴AF===2,CF=BC-BF=6-4=2=DE.
在△ADE和△DCF中,
∴△ADE≌△DCF(SAS),
∴∠DAE=∠CDF.
∵∠DAE+∠AED=90°,
∴∠EDG+∠DEG=90°,即∠AGF=∠DGE=90°.
∵H为AF的中点,
∴GH=AF=,
故选A.
例2 C
提示:在正方形ABCD中,∠B=90°,
∴AB2+CB2=AC2.
∵AB=CB,AC=20,
∴2AB2=(20)2,
∴AB=20.
在菱形ABCD中,AB=CB=20,∠B=60°,
∴△ABC是等边三角形,∴AC=AB=20.
如图,连接BD交AC于点O,
∴AC⊥BD,∠ABO=30°,
∴OA=AB=10,
∴OB=OA=10,
∴BD=2OB=20,故选C.
变式训练
1.A 提示:如图,连接AC,BD.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,EF是△ABC的中位线,
∴EH=BD,EH∥BD,FG=BD,FG∥BD,EF=AC,
∴EH=FG,EH∥FG,∴四边形EFGH为平行四边形.
当α=90°时,四边形ABCD为矩形,则AC=BD,
∴EH=EF,此时平行四边形EFGH为菱形,
∴α从0°逐渐增大到180°的过程中,四边形EFGH形状的变化依次是平行四边形→菱形→平行四边形,故选A.
2.(1)平行四边形 (2)①50 ②13
提示:(1)∵△ABC和△FDE都是边长为10 cm的等边三角形,
∴AC=DF,∠ACD=∠FDE=60°,
∴AC∥DF,
∴四边形ADFC是平行四边形.
(2)①当四边形ADFC是菱形时,点B与点D重合,
∴t=3 s时,平行四边形ADFC是菱形,
∴AD=DF.
此时,S菱形ADFC=2S△ABC=2××102=50(cm2).
②当点B与点E重合时,AF=DC,AE=EF=DE=EC,
则四边形ADFC是矩形,如图所示,
此时,t=(3+10)÷1=13(s),
∴t=13 s时,四边形ADFC是矩形.
(6年7考,2~3分)
在最近三年的中考选择题中,以图中标注数据、判断画图方案、补充证明过程等不同方式考查平行四边形的判定.特殊四边形主要考查矩形、菱形、正方形的性质,涉及图形的剪裁、拼接等.一般在选择题和填空题中出现,考查基本性质与判定,也在探究题中作为铺垫性内容,考查将复杂图形转化为基本图形解决问题的能力.河北省近5年都在选择题中出现,预测2025年河北省中考仍将延续这一命题特点.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点特殊四边形的性质与判定 (常考点)
特殊四边形 平行四边形 矩形 菱形 正方形
图形
性质 1.对边① . 2.两组对角分别相等. 3.对角线互相平分. 4.中心对称图形. 5.周长C=2(a+b),面积S=ah 1.对边平行且相等. 2.四个角都是② . 3.对角线互相平分且相等. 4.既是中心对称图形,也是轴对称图形,有2条对称轴. 5.周长C=2(a+b),面积S=ab 1.四条边③ . 2.两组对角分别相等. 3.对角线互相④ ,且平分⑤ . 4.既是中心对称图形,也是轴对称图形,有2条对称轴. 5.周长C=4a,面积S=ah=mn 1.四条边相等. 2.四个角都是直角. 3.对角线互相垂直平分且相等,平分一组对角. 4.既是中心对称图形,也是轴对称图形,有4条对称轴. 5.周长C=4a, 面积S=a2=m2
判定 1.定义法:两组对边分别平行的四边形. 2.两组对边分别相等的四边形. 3.一组对边⑥ 的四边形. 4.两组对角分别相等的四边形. 5.两条对角线互相平分的四边形 1.定义法:有一个角是⑦ 的平行四边形. 2.有三个角是直角的四边形. 3.对角线⑧ 的平行四边形 1.定义法:有一组邻边⑨ 的平行四边形. 2.四条边都相等的四边形. 3.对角线互相⑩ 的平行四边形 1.定义法:有一个角是直角,且有一组邻边相等的平行四边形. 2.一组邻边相等的矩形. 3.有一个角是直角的菱形. 4.对角线相等且互相垂直、平分的四边形
【基础演练】
1.(北师九上P26第4题变式)已知菱形的两条对角线长分别是7和8,则菱形的面积是 ( )
A.56 B.28
C.15 D.20
2.(北师九上P13第2题变式)如图,在矩形ABCD中,对角线AC,BD相交于点O,若AB=2,∠AOB=60°,则AC的长为 ( )
A.2
B.3
C.4
D.6
3.如图,在平行四边形ABCD中,下列结论错误的是 ( )
A.AD∥BC
B.AB=DC
C.∠DAB=∠BCD
D.AC=BD
4.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED的度数为 ( )
A.15°
B.30°
C.45°
D.60°
5.(北师九上P29第20题改编)小琦在复习几种特殊四边形的关系时整理如图所示,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是 ( )
A.(1)处可填∠A=90°
B.(2)处可填AD=AB
C.(3)处可填DC=CB
D.(4)处可填∠B=∠D
真题精粹·重变式——河北6年真题精选及拓展
考向1特殊四边形的判定 (6年4考)
1.(2022·河北8题3分)依据所标数据,下列一定为平行四边形的是 ( )
A B
C D
2.(2023·河北8题2分)综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.图1~图3是其作图过程.
(1)作BD的垂直平分线交BD于点O;
(2)连接AO,在AO的延长线上截取OC=AO;
(3)连接DC,BC,则四边形ABCD即所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是 ( )
A.两组对边分别平行
B.两组对边分别相等
C.对角线互相平分
D.一组对边平行且相等
3.(2024·河北10题2分)下面是嘉嘉作业本上的一道习题及解答过程:
如图,在△ABC中,AB=AC,AE平分△ABC的外角∠CAN,M是AC的中点,连接BM并延长交AE于点D,连接CD. 求证:四边形ABCD是平行四边形. 证明:∵AB=AC, ∴∠ABC=∠3. ∵∠CAN=∠ABC+∠3,∠CAN=∠1+∠2,∠1=∠2, ∴① . 又∵∠4=∠5,MA=MC, ∴△MAD≌△MCB(② ), ∴MD=MB,∴四边形ABCD是平行四边形.
若以上解答过程正确,则①,②应分别为 ( )
A.∠1=∠3,AAS
B.∠1=∠3,ASA
C.∠2=∠3,AAS
D.∠2=∠3,ASA
4.(2020·河北10题3分)如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成了平行四边形,并推理如下:
点A,C分别转到了点C,A处, 而点B转到了点D处. ∵CB=AD, ∴四边形ABCD是平行四边形.
小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形……”之间作补充.下列选项中正确的是 ( )
A.嘉淇推理严谨,不必补充
B.应补充:且AB=CD
C.应补充:且AB∥CD
D.应补充:且OA=OC
考向2特殊四边形的性质 (6年3考)
5.(2019·河北5题3分)如图,在菱形ABCD中,∠D=150°,则∠1的度数为 ( )
A.30° B.25° C.20° D.15°
6.(2023·河北11题2分)如图,在Rt△ABC中,AB=4,M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC= ( )
A.4
B.8
C.12
D.16
核心突破·拓思维——学科核心素养提升
题型1 特殊四边形的三要素
(2024·邯郸二模)在 ABCD中,EF经过两条对角线的交点O,分别交AB,CD于点E,F,在对角线AC上通过作图得到点M,N,如图1,图2,下面关于以F,M,E,N为顶点的四边形的形状的说法正确的是 ( )
图1 以点O为圆心,OE的长为半径作弧,交AC于点M,N 图2 过点E作EM⊥AC于点M,过点F作FN⊥AC于点N
A.都为矩形
B.都为菱形
C.图1为矩形,图2为平行四边形
D.图1为矩形,图2为菱形
无论是特殊的平行四边形,还是一般的平行四边形,命题的着眼点都在于它们的边、角和对角线三个基本要素,这也是反映它们的定义、性质和判定方法的研究方向.在具体的题目中,三要素的考查各有侧重,信息的呈现方式灵活多样.可以在选择题中单独考查,也可以在解答题中作为重要的构图内容进行考查.除三要素外,它们的对称性、面积也时有考查.
1.斜边为2的两个全等的含30°的直角三角板,按照如图1所示的方式拼成一个矩形,将一个三角板保持不动,另一个三角板沿斜边向右下方向滑动,当四边形ABCD是菱形时,如图2,则平移距离AE的长为 ( )
A.1 B.
C. D.2
2.如图,正方形ABCD的边长为6,点E,F分别在DC,BC上,BF=CE,连接AE,DF,AE与DF相交于点G,连接AF,取AF的中点H,连接HG,若AE=2,则GH的长为 ( )
A. B.2
C.2 D.4
题型2 特殊四边形之间的联系与转化
(2024·石家庄一模)小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为如图1所示的菱形,并测得∠B=60°,接着活动学具成为如图2所示的正方形,并测得对角线AC=20,则图1中菱形的对角线BD的长为 ( )
A.20 B.30
C.20 D.20
只要证明EA=ED即可解决问题.
由正方形的性质结合勾股定理先后求出DE及CE的长,由BF=CE,根据勾股定理求AF的长,证明△ADE≌△DCF(SAS),得出∠DAE=∠CDF,求出∠AGF=∠DGE=90°,再由直角三角形的性质即可得出答案.
矩形、菱形、正方形之间,以及它们与平行四边形之间有着密切的关系,可以通过边、角、对角线的变化进行转化,特别是由一般到特殊的转化,体现了知识之间的内在联系.此类问题在中考试卷上,经常以动态操作的方式呈现,解题时要注意在操作过程中保持不变的数量关系或位置关系,以及动态变化过程中的特殊时刻.
特殊的四边形从属关系图
1.如图,在 ABCD中,∠ABC=α,BC>AB,E,F,G,H分别是AB,BC,CD,DA的中点,顺次连接E,F,G,H,在α从0°逐渐增大到180°的过程中,四边形EFGH形状的变化依次是 ( )
A.平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形
C.平行四边形→菱形→正方形→平行四边形
D.平行四边形→矩形→正方形→平行四边形
2.如图,已知△ABC和△DEF是两个边长都为10 cm的等边三角形,且点B,D,C,E都在一条直线上,连接AD,CF.
(1)四边形ADFC的形状是 .
(2)若BD=3 cm,此时△ABC沿着BE方向以1 cm/s的速度运动,运动时间为t.
①当四边形ADFC是菱形时,它的面积是 cm2;
②当运动时间t= s时,四边形ADFC是矩形.
(1)通过一组对边AC与DF平行且相等,判定四边形ADFC的形状.
(2)①根据菱形的性质可知此时点B与点D重合,则菱形的面积等于2个等边三角形的面积和;
②根据矩形的判定条件可知此时的对角线相等,则点B与点E重合,画图求解.
参考答案
考点清单
①平行且相等 ②直角 ③相等 ④平分且垂直
⑤一组对角 ⑥平行且相等 ⑦直角 ⑧相等
⑨相等 ⑩垂直
基础演练
1.B 2.C 3.D 4.C 5.D
真题精粹·重变式
1.D 2.C 3.D 4.B 5.D 6.B
核心突破·拓思维
例1 C
提示:在 ABCD中,AB∥DC,OA=OC,
∴∠FCO=∠EAO,∠CFO=∠AEO.
在△FCO和△EAO中,
∴△FCO≌△EAO(AAS),
∴OE=OF.
由图1作图可得OE=OF=OM=ON,
∴图1中以F,M,E,N为顶点的四边形为矩形.
由图2作图可得EM⊥AC,FN⊥AC,
∴∠EMO=∠FNO=90°.
在△OME和△ONF中,
∴△OME≌△ONF(AAS),
∴OM=ON.
又∵OE=OF,
∴图2中以F,M,E,N为顶点的四边形为平行四边形,故选C.
变式训练
1.A
2.A 提示:∵四边形ABCD为正方形,
∴AB=BC=CD=AD=6,∠B=∠C=∠ADE=90°,
∴DE===2,
∴BF=CE=CD-DE=6-2=4,
∴AF===2,CF=BC-BF=6-4=2=DE.
在△ADE和△DCF中,
∴△ADE≌△DCF(SAS),
∴∠DAE=∠CDF.
∵∠DAE+∠AED=90°,
∴∠EDG+∠DEG=90°,即∠AGF=∠DGE=90°.
∵H为AF的中点,
∴GH=AF=,
故选A.
例2 C
提示:在正方形ABCD中,∠B=90°,
∴AB2+CB2=AC2.
∵AB=CB,AC=20,
∴2AB2=(20)2,
∴AB=20.
在菱形ABCD中,AB=CB=20,∠B=60°,
∴△ABC是等边三角形,∴AC=AB=20.
如图,连接BD交AC于点O,
∴AC⊥BD,∠ABO=30°,
∴OA=AB=10,
∴OB=OA=10,
∴BD=2OB=20,故选C.
变式训练
1.A 提示:如图,连接AC,BD.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,EF是△ABC的中位线,
∴EH=BD,EH∥BD,FG=BD,FG∥BD,EF=AC,
∴EH=FG,EH∥FG,∴四边形EFGH为平行四边形.
当α=90°时,四边形ABCD为矩形,则AC=BD,
∴EH=EF,此时平行四边形EFGH为菱形,
∴α从0°逐渐增大到180°的过程中,四边形EFGH形状的变化依次是平行四边形→菱形→平行四边形,故选A.
2.(1)平行四边形 (2)①50 ②13
提示:(1)∵△ABC和△FDE都是边长为10 cm的等边三角形,
∴AC=DF,∠ACD=∠FDE=60°,
∴AC∥DF,
∴四边形ADFC是平行四边形.
(2)①当四边形ADFC是菱形时,点B与点D重合,
∴t=3 s时,平行四边形ADFC是菱形,
∴AD=DF.
此时,S菱形ADFC=2S△ABC=2××102=50(cm2).
②当点B与点E重合时,AF=DC,AE=EF=DE=EC,
则四边形ADFC是矩形,如图所示,
此时,t=(3+10)÷1=13(s),
∴t=13 s时,四边形ADFC是矩形.
同课章节目录
