【中考考点探究】第2节 概率 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第2节 概率 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 289.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:39:44 | ||
图片预览




文档简介
第2节 概率
(6年6考,2~10分)
概率是河北省中考必考内容,既会在选择题或填空题中单独考查,也会出现在解答题中,与统计或其他知识综合考查.2021年和2024年都有以概率为主的解答题,2019年和2020年出现概率与其他知识综合的解答题,总体来看,概率的地位有所提升.预测2025年河北省中考对于统计与概率两个主题的考查会综合考虑,统筹布局,总分控制在12~14分.在实际问题中考查概率的计算,关键在于采用适当的方法列举所有等可能出现的结果.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1随机事件与概率
概率 定义:表示一个事件发生的可能性大小的数值
事件的类型及其概率 必然事件 ①
② 0
不确定性事件(随机事件) ③考点2随机事件概率的计算 (轮考点)
随机事件概率的计算 公式法 P(A)=(m表示试验中事件A出现的次数,n表示所有等可能出现的结果的次数)
直接列举法 当一次试验中可能出现的结果数量有限且各种结果出现的可能性相等时
⑤ 当一次试验涉及两个因素,并且可能出现的结果数较多时
画树状图法 当一次试验涉及两个或更多因素(例如从3个口袋中取球)时
用频率估计概率 在大量重复试验条件下,事件发生的频率会在某个常数附近摆动时,可用其频率估计概率
【基础演练】
1.(人教九上P128练习变式)下列语句所描述的事件是随机事件的是 ( )
A.两点决定一直线
B.清明时节雨纷纷
C.没有水分,种子发芽
D.太阳从东方升起
2.中国古代数学有着辉煌的成就,《周髀算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献.某中学拟从这四部数学名著中选择一部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是 ( )
A. B. C. D.
3.(北师七下P151议一议变式)如图,这是由6个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是 ( )
A. B. C. D.1
4.(北师九上P62第2题变式)不透明的袋子中有3个小球,其中有1个红球,1个黄球,1个绿球,除颜色外3个小球无其他区别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么两次摸出的小球都是红球的概率是 ( )
A. B.
C. D.
5.一个不透明的布袋中装有除颜色外均相同的14个黑球,5个白球和若干个红球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,则袋中红球有 个.
真题精粹·重变式——河北6年真题精选及拓展
考向1可能性的大小 (6年1考)
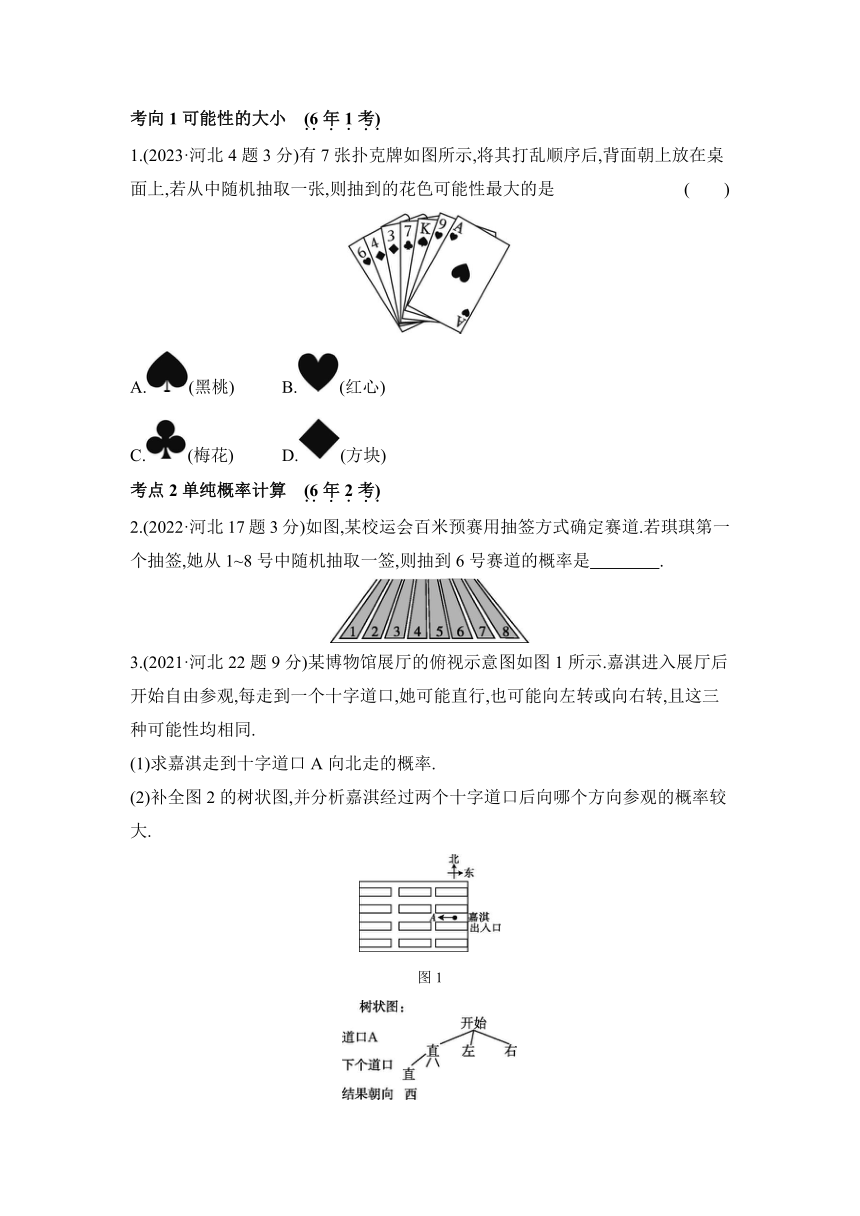
1.(2023·河北4题3分)有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上,若从中随机抽取一张,则抽到的花色可能性最大的是 ( )
A.(黑桃) B.(红心)
C.(梅花) D.(方块)
考点2单纯概率计算 (6年2考)
2.(2022·河北17题3分)如图,某校运会百米预赛用抽签方式确定赛道.若琪琪第一个抽签,她从1~8号中随机抽取一签,则抽到6号赛道的概率是 .
3.(2021·河北22题9分)某博物馆展厅的俯视示意图如图1所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,她可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1)求嘉淇走到十字道口A向北走的概率.
(2)补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.
图1
图2
考点3统计与概率结合 (6年1考)
4.(2024·河北21题9分)甲、乙、丙三张卡片正面分别写有a+b,2a+b,a-b,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当a=1,b=-2时,求取出的卡片上代数式的值为负数的概率.
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
a+b 2a+b a-b
a+b 2a+2b 2a
2a+b
a-b 2a
5.(2019·河北22题9分)某球室有三种品牌的4个乒乓球,价格(单位:元)是7,8,9三种.从中随机拿出一个球,已知P(一次拿到8元球)=.
(1)求这4个球的价格的众数.
(2)若甲组已拿走一个7元球训练,乙组准备从剩余的3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球的价格的中位数是否相同 请简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如下表)求乙组两次都拿到8元球的概率.
考点4数轴与概率结合 (6年1考)
6.(2020·河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.
移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位长度,同时乙向西移动1个单位长度;
②若甲对乙错,则甲向东移动4个单位长度,同时乙向东移动2个单位长度;
③若甲错乙对,则甲向西移动2个单位长度,同时乙向西移动4个单位长度.
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P.
(2)从如图所示的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值.
(3)从如图所示的位置开始,若进行了k次
移动游戏后,甲与乙的位置相距2个单位长度,直接写出k的值.
核心突破·拓思维——学科核心素养提升
题型 求实际问题中的概率
(2024 廊坊一模)某中学对九年级100名学生进行了“是否喜欢打羽毛球”的问卷调查,得到下表:
已知在这100人中随机抽取1人,抽到喜欢打羽毛球的学生的概率为.
(1)请将上表补充完整.
(2)现有A,B,C,D 4名喜欢打羽毛球的同学,其中2名男生2名女生,若从这4人中随机挑选2人参加比赛,请用列表法求出选中一男一女的概率.
(3)若将(2)中A,B,C,D 4名同学分成两组参加比赛,每组两人,请直接写出A与D在一组的概率.
概率与统计属于同一知识领域,在河北省中考试卷上共占“一大一小”两道题,即一道填空或选择题,一道解答题.两个知识的考查位置不确定,主要是在现实情境中利用列举法求解古典概型问题,在解答题中常用画树状图法或列表法求概率.有时统计与概率会在同一道解答题中综合考查.
(1)根据概率公式可知,喜欢打羽毛球的学生人数=总人数×相应概率
↓
计算喜欢打羽毛球的男生人数
↓
求得不喜欢打羽毛球的女生人数
↓
(2)用列表或者画树状图的方法,列举出所有等可能的情况
↓
从中找到选中一男一女的结果数
↓
根据概率公式计算
↓
(3)选取4人中的两个为一组,另两个自然作为另一组,列举出各种对阵情况
↓
利用概率公式求解
计算事件概率的常用方法
2025年春节期间调研小组随机调查了某新开放景区的部分参观群众,请参观群众为本景区打分(打分按从高到低分为5个分值:5分,4分,3分,2分,1分),并将调查结果绘制成不完整的条形统计图(如图1)和扇形统计图(如图2).根据以上信息,回答下列问题:
(1)本次共调查了 名参观群众,请补全条形统计图,分值的众数是 ,中位数是 .
(2)为了进一步研究,调研小组又增加调查了5位参观者,若他们的打分分别为5,4,4,5,3,则增加调查人数前后,本次活动打分分值的中位数与原来是否相同 请判断并简要说明理由.
(3)若从打分较低的四人中随机抽取2人做情况反馈,发现抽取的2人恰为一成人一儿童的概率为,直接写出这4人中成人与儿童的可能分布情况.
(1)由“4分”对应的人数及其所占百分比求出总人数
↓
求“5分” 对应的人数,补全条形统计图
↓
利用条形图中数据求众数和中位数
↓
(2)求增加后的总人数和每个分数段的人数
↓
根据中位数的定义求解说明
↓
(3)用列表或画树状图的方法列举所有情况,结合概率公式推算
易错警示:
(3)中,不要轻易认为成人与儿童各占一半,得到“2名成人2名儿童”的错误结论在此情况下,抽取的2人恰为一成人一儿童的概率为 .
参考答案
考点清单
①1 ②不可能事件 ③0 ④1 ⑤列表法
基础演练
1.B 2.C 3.B 4.D
5.6
真题精粹·重变式
1.B
2.
3.(1)嘉淇走到十字道口A向北走的概率为.
(2)补全树状图如下:
共有9种等可能的结果,嘉淇经过两个十字道口后向西参观的结果有3种、向南参观的结果有2种、向北参观的结果有2种、向东参观的结果有2种,
∴向西参观的概率为=,向南参观的概率=向北参观的概率=向东参观的概率=,
∴向西参观的概率大.
4.(1)当a=1,b=-2时,a+b=-1,2a+b=0,a-b=3.
从三张卡片中随机抽取一张,共有3种等可能的结果,其中取出的卡片上代数式的值为负数的结果有1种,
∴取出的卡片上代数式的值为负数的概率为.
(2)补全表格如下:
a+b 2a+b a-b
a+b 2a+2b 3a+2b 2a
2a+b 3a+2b 4a+2b 3a
a-b 2a 3a 2a-2b
共有9种等可能的结果,其中和为单项式的结果有2a,3a,2a,3a,共4种,
∴和为单项式的概率为.
5.(1)∵P(一次拿到8元球)=,
∴8元球的个数为4×=2(个),按照从小到大的顺序排列为7,8,8,9,
∴这4个球的价格的众数为8.
(2)①所剩的3个球的价格的中位数与原来4个球的价格的中位数相同.理由如下:
∵原来4个球的价格按照从小到大的顺序排列为7,8,8,9,
∴原来4个球的价格的中位数为=8.
∵所剩的3个球的价格为8,8,9,
∴所剩的3个球的价格的中位数为8,
∴所剩的3个球的价格的中位数与原来4个球的价格的中位数相同.
②列表如下:
8 8 9
8 8,8 8,8 8,9
8 8,8 8,8 8,9
9 9,8 9,8 9,9
由表格可知共有9种等可能的结果,乙组两次都拿到8元球的结果有4种,
∴乙组两次都拿到8元球的概率为.
6.(1)第一次移动游戏有4种等可能的结果,分别是甲、乙都对,甲、乙都错,甲对乙错,甲错乙对.
∵甲的位置停留在正半轴上,只有-3+4=1,即甲对乙错这1种结果,
∴P=.
(2)根据题意可知乙答了10次,答对了n次,则答错了(10-n)次.
根据题意可得,n次答对,向西移动4n个单位长度,
(10-n)次答错,向东移动2(10-n)个单位长度,
∴m=5-4n+2(10-n)=25-6n.
当m=0时,由25-6n=0,解得n=,即n=4.
∵n表示次数,只能取整数,
∴当n=4时,距离原点最近.
(3)3或5.
提示:初始位置中,甲、乙的距离是8个单位长度,
由题意可知,当甲、乙一对一错时,二者之间距离缩小2个单位长度;当甲、乙同时答对或同时答错时,二者之间的距离也是缩小2个单位长度,
∴当甲、乙位置相距2个单位长度时,共缩小了6个单位长度或10个单位长度.
∵6÷2=3,10÷2=5,
∴k的值为3或5.
核心突破·拓思维
例(1)由题意可知,喜欢打羽毛球的学生人数为100×=80,
则喜欢打羽毛球的男生人数为80-30=50,
所以不喜欢打羽毛球的女生人数为100-(50+30+5)=15,
补全表格如下:
(2)列表如下:
男1男2女1女2
男1——(男2,男1)(女1,男1)(女2,男1)
男2(男1,男2)——(女1,男2)(女2,男2)
女1(男1,女1)(男2,女1)——(女2,女1)
女2(男1,女2)(男2,女2)(女1,女2)——
得到所有等可能的情况有12种,其中恰好抽中一男一女的情况有8种,所以恰好选中一男一女的概率为=.
(3)根据题意可知,所有等可能的情况有3种,分别是AB-CD,AC-BD,AD-BC,所以A与D能分在一起的概率为.
变式训练
(1)30;5;4.5.
提示:本次被调查的总人数是11÷=30,
∴打5分的人数为30-11-2-1-1=15,
∴众数为5分,中位数为=4.5(分).
补全统计图如下:
(2)不相同.
理由:增加人数后,各个分数段的人数为5分17人,4分13人,3分3人,2分1人,1分1人,共35人,
∴中位数是4分,发生了改变.
(3)3名成人1名儿童,或3名儿童1名成人.
提示:3名成人(或儿童)分别用A1,A2,A3表示,一名儿童(或成人)用B表示,画出树状图如图所示:
由树状图可知,共有12种可能的情况,并且抽取的2人恰为一成人一儿童的情况有6种,则抽取的2人恰为一成人一儿童的概率为.
(6年6考,2~10分)
概率是河北省中考必考内容,既会在选择题或填空题中单独考查,也会出现在解答题中,与统计或其他知识综合考查.2021年和2024年都有以概率为主的解答题,2019年和2020年出现概率与其他知识综合的解答题,总体来看,概率的地位有所提升.预测2025年河北省中考对于统计与概率两个主题的考查会综合考虑,统筹布局,总分控制在12~14分.在实际问题中考查概率的计算,关键在于采用适当的方法列举所有等可能出现的结果.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1随机事件与概率
概率 定义:表示一个事件发生的可能性大小的数值
事件的类型及其概率 必然事件 ①
② 0
不确定性事件(随机事件) ③
随机事件概率的计算 公式法 P(A)=(m表示试验中事件A出现的次数,n表示所有等可能出现的结果的次数)
直接列举法 当一次试验中可能出现的结果数量有限且各种结果出现的可能性相等时
⑤ 当一次试验涉及两个因素,并且可能出现的结果数较多时
画树状图法 当一次试验涉及两个或更多因素(例如从3个口袋中取球)时
用频率估计概率 在大量重复试验条件下,事件发生的频率会在某个常数附近摆动时,可用其频率估计概率
【基础演练】
1.(人教九上P128练习变式)下列语句所描述的事件是随机事件的是 ( )
A.两点决定一直线
B.清明时节雨纷纷
C.没有水分,种子发芽
D.太阳从东方升起
2.中国古代数学有着辉煌的成就,《周髀算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献.某中学拟从这四部数学名著中选择一部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是 ( )
A. B. C. D.
3.(北师七下P151议一议变式)如图,这是由6个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是 ( )
A. B. C. D.1
4.(北师九上P62第2题变式)不透明的袋子中有3个小球,其中有1个红球,1个黄球,1个绿球,除颜色外3个小球无其他区别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么两次摸出的小球都是红球的概率是 ( )
A. B.
C. D.
5.一个不透明的布袋中装有除颜色外均相同的14个黑球,5个白球和若干个红球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,则袋中红球有 个.
真题精粹·重变式——河北6年真题精选及拓展
考向1可能性的大小 (6年1考)
1.(2023·河北4题3分)有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上,若从中随机抽取一张,则抽到的花色可能性最大的是 ( )
A.(黑桃) B.(红心)
C.(梅花) D.(方块)
考点2单纯概率计算 (6年2考)
2.(2022·河北17题3分)如图,某校运会百米预赛用抽签方式确定赛道.若琪琪第一个抽签,她从1~8号中随机抽取一签,则抽到6号赛道的概率是 .
3.(2021·河北22题9分)某博物馆展厅的俯视示意图如图1所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,她可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1)求嘉淇走到十字道口A向北走的概率.
(2)补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.
图1
图2
考点3统计与概率结合 (6年1考)
4.(2024·河北21题9分)甲、乙、丙三张卡片正面分别写有a+b,2a+b,a-b,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当a=1,b=-2时,求取出的卡片上代数式的值为负数的概率.
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
a+b 2a+b a-b
a+b 2a+2b 2a
2a+b
a-b 2a
5.(2019·河北22题9分)某球室有三种品牌的4个乒乓球,价格(单位:元)是7,8,9三种.从中随机拿出一个球,已知P(一次拿到8元球)=.
(1)求这4个球的价格的众数.
(2)若甲组已拿走一个7元球训练,乙组准备从剩余的3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球的价格的中位数是否相同 请简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如下表)求乙组两次都拿到8元球的概率.
考点4数轴与概率结合 (6年1考)
6.(2020·河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.
移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位长度,同时乙向西移动1个单位长度;
②若甲对乙错,则甲向东移动4个单位长度,同时乙向东移动2个单位长度;
③若甲错乙对,则甲向西移动2个单位长度,同时乙向西移动4个单位长度.
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P.
(2)从如图所示的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值.
(3)从如图所示的位置开始,若进行了k次
移动游戏后,甲与乙的位置相距2个单位长度,直接写出k的值.
核心突破·拓思维——学科核心素养提升
题型 求实际问题中的概率
(2024 廊坊一模)某中学对九年级100名学生进行了“是否喜欢打羽毛球”的问卷调查,得到下表:
已知在这100人中随机抽取1人,抽到喜欢打羽毛球的学生的概率为.
(1)请将上表补充完整.
(2)现有A,B,C,D 4名喜欢打羽毛球的同学,其中2名男生2名女生,若从这4人中随机挑选2人参加比赛,请用列表法求出选中一男一女的概率.
(3)若将(2)中A,B,C,D 4名同学分成两组参加比赛,每组两人,请直接写出A与D在一组的概率.
概率与统计属于同一知识领域,在河北省中考试卷上共占“一大一小”两道题,即一道填空或选择题,一道解答题.两个知识的考查位置不确定,主要是在现实情境中利用列举法求解古典概型问题,在解答题中常用画树状图法或列表法求概率.有时统计与概率会在同一道解答题中综合考查.
(1)根据概率公式可知,喜欢打羽毛球的学生人数=总人数×相应概率
↓
计算喜欢打羽毛球的男生人数
↓
求得不喜欢打羽毛球的女生人数
↓
(2)用列表或者画树状图的方法,列举出所有等可能的情况
↓
从中找到选中一男一女的结果数
↓
根据概率公式计算
↓
(3)选取4人中的两个为一组,另两个自然作为另一组,列举出各种对阵情况
↓
利用概率公式求解
计算事件概率的常用方法
2025年春节期间调研小组随机调查了某新开放景区的部分参观群众,请参观群众为本景区打分(打分按从高到低分为5个分值:5分,4分,3分,2分,1分),并将调查结果绘制成不完整的条形统计图(如图1)和扇形统计图(如图2).根据以上信息,回答下列问题:
(1)本次共调查了 名参观群众,请补全条形统计图,分值的众数是 ,中位数是 .
(2)为了进一步研究,调研小组又增加调查了5位参观者,若他们的打分分别为5,4,4,5,3,则增加调查人数前后,本次活动打分分值的中位数与原来是否相同 请判断并简要说明理由.
(3)若从打分较低的四人中随机抽取2人做情况反馈,发现抽取的2人恰为一成人一儿童的概率为,直接写出这4人中成人与儿童的可能分布情况.
(1)由“4分”对应的人数及其所占百分比求出总人数
↓
求“5分” 对应的人数,补全条形统计图
↓
利用条形图中数据求众数和中位数
↓
(2)求增加后的总人数和每个分数段的人数
↓
根据中位数的定义求解说明
↓
(3)用列表或画树状图的方法列举所有情况,结合概率公式推算
易错警示:
(3)中,不要轻易认为成人与儿童各占一半,得到“2名成人2名儿童”的错误结论在此情况下,抽取的2人恰为一成人一儿童的概率为 .
参考答案
考点清单
①1 ②不可能事件 ③0 ④1 ⑤列表法
基础演练
1.B 2.C 3.B 4.D
5.6
真题精粹·重变式
1.B
2.
3.(1)嘉淇走到十字道口A向北走的概率为.
(2)补全树状图如下:
共有9种等可能的结果,嘉淇经过两个十字道口后向西参观的结果有3种、向南参观的结果有2种、向北参观的结果有2种、向东参观的结果有2种,
∴向西参观的概率为=,向南参观的概率=向北参观的概率=向东参观的概率=,
∴向西参观的概率大.
4.(1)当a=1,b=-2时,a+b=-1,2a+b=0,a-b=3.
从三张卡片中随机抽取一张,共有3种等可能的结果,其中取出的卡片上代数式的值为负数的结果有1种,
∴取出的卡片上代数式的值为负数的概率为.
(2)补全表格如下:
a+b 2a+b a-b
a+b 2a+2b 3a+2b 2a
2a+b 3a+2b 4a+2b 3a
a-b 2a 3a 2a-2b
共有9种等可能的结果,其中和为单项式的结果有2a,3a,2a,3a,共4种,
∴和为单项式的概率为.
5.(1)∵P(一次拿到8元球)=,
∴8元球的个数为4×=2(个),按照从小到大的顺序排列为7,8,8,9,
∴这4个球的价格的众数为8.
(2)①所剩的3个球的价格的中位数与原来4个球的价格的中位数相同.理由如下:
∵原来4个球的价格按照从小到大的顺序排列为7,8,8,9,
∴原来4个球的价格的中位数为=8.
∵所剩的3个球的价格为8,8,9,
∴所剩的3个球的价格的中位数为8,
∴所剩的3个球的价格的中位数与原来4个球的价格的中位数相同.
②列表如下:
8 8 9
8 8,8 8,8 8,9
8 8,8 8,8 8,9
9 9,8 9,8 9,9
由表格可知共有9种等可能的结果,乙组两次都拿到8元球的结果有4种,
∴乙组两次都拿到8元球的概率为.
6.(1)第一次移动游戏有4种等可能的结果,分别是甲、乙都对,甲、乙都错,甲对乙错,甲错乙对.
∵甲的位置停留在正半轴上,只有-3+4=1,即甲对乙错这1种结果,
∴P=.
(2)根据题意可知乙答了10次,答对了n次,则答错了(10-n)次.
根据题意可得,n次答对,向西移动4n个单位长度,
(10-n)次答错,向东移动2(10-n)个单位长度,
∴m=5-4n+2(10-n)=25-6n.
当m=0时,由25-6n=0,解得n=,即n=4.
∵n表示次数,只能取整数,
∴当n=4时,距离原点最近.
(3)3或5.
提示:初始位置中,甲、乙的距离是8个单位长度,
由题意可知,当甲、乙一对一错时,二者之间距离缩小2个单位长度;当甲、乙同时答对或同时答错时,二者之间的距离也是缩小2个单位长度,
∴当甲、乙位置相距2个单位长度时,共缩小了6个单位长度或10个单位长度.
∵6÷2=3,10÷2=5,
∴k的值为3或5.
核心突破·拓思维
例(1)由题意可知,喜欢打羽毛球的学生人数为100×=80,
则喜欢打羽毛球的男生人数为80-30=50,
所以不喜欢打羽毛球的女生人数为100-(50+30+5)=15,
补全表格如下:
(2)列表如下:
男1男2女1女2
男1——(男2,男1)(女1,男1)(女2,男1)
男2(男1,男2)——(女1,男2)(女2,男2)
女1(男1,女1)(男2,女1)——(女2,女1)
女2(男1,女2)(男2,女2)(女1,女2)——
得到所有等可能的情况有12种,其中恰好抽中一男一女的情况有8种,所以恰好选中一男一女的概率为=.
(3)根据题意可知,所有等可能的情况有3种,分别是AB-CD,AC-BD,AD-BC,所以A与D能分在一起的概率为.
变式训练
(1)30;5;4.5.
提示:本次被调查的总人数是11÷=30,
∴打5分的人数为30-11-2-1-1=15,
∴众数为5分,中位数为=4.5(分).
补全统计图如下:
(2)不相同.
理由:增加人数后,各个分数段的人数为5分17人,4分13人,3分3人,2分1人,1分1人,共35人,
∴中位数是4分,发生了改变.
(3)3名成人1名儿童,或3名儿童1名成人.
提示:3名成人(或儿童)分别用A1,A2,A3表示,一名儿童(或成人)用B表示,画出树状图如图所示:
由树状图可知,共有12种可能的情况,并且抽取的2人恰为一成人一儿童的情况有6种,则抽取的2人恰为一成人一儿童的概率为.
同课章节目录
