【中考考点探究】第2节 与圆有关的位置关系 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第2节 与圆有关的位置关系 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:43:27 | ||
图片预览


文档简介
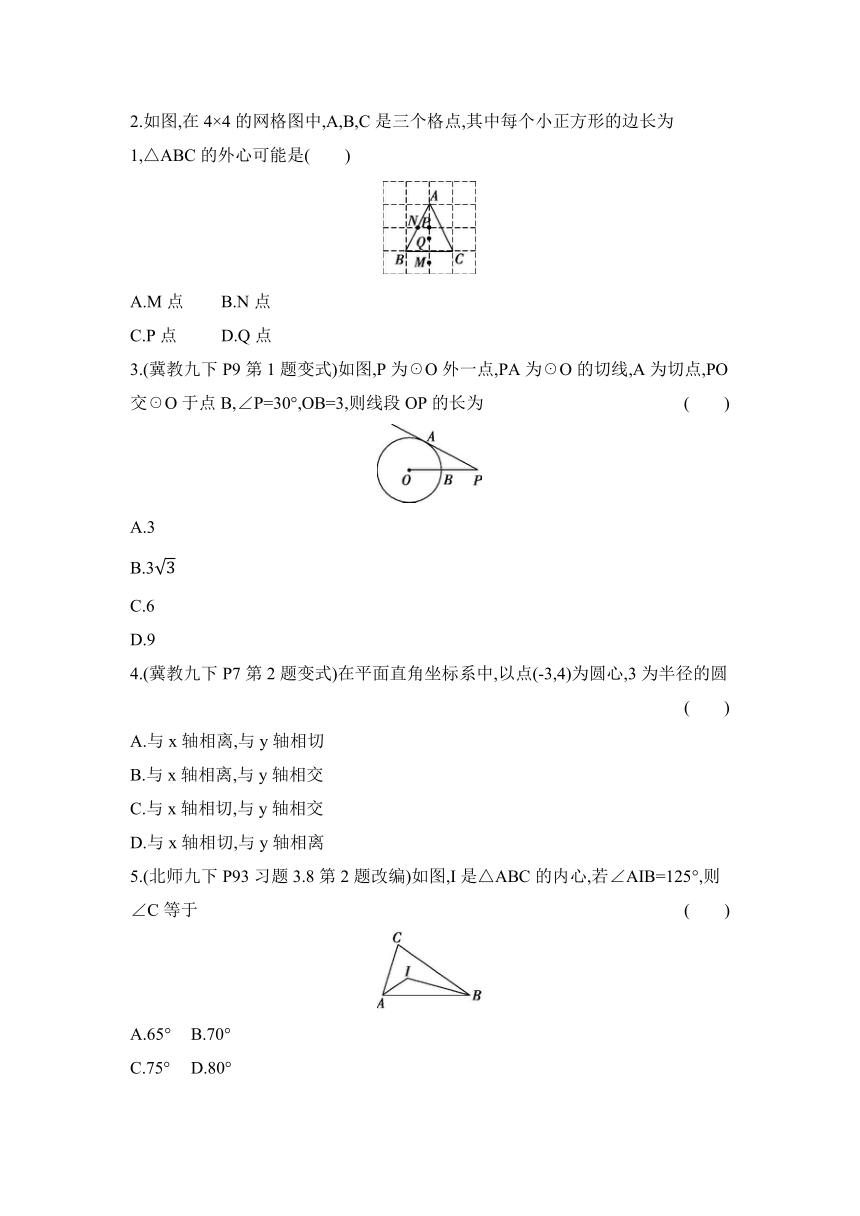
第2节 与圆有关的位置关系
(6年10考,2~10分)
与圆有关的位置关系涉及的知识点很多,其中切线的性质是重中之重.预测2025年中考的解答题中,仍会考查切线的性质,并与其他几何知识组合成为圆的综合题,而且考查难度增大.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1与圆有关的位置关系
点与圆的 位置关系 设点到圆心的距离为d 1.d① r 点在☉O内. 2.d② r 点在☉O上. 3.d③ r 点在☉O外
直线与 圆的位 置关系 位置关系 相离 相切 相交
图形
公共点个数 0 1 2
数量关系 d>r d=r d考点2切线 (常考点)
切线的判定 1.与圆只有一个公共点的直线是圆的切线(定义法). 2.到圆心的距离等于④ 的直线是圆的切线. 3.经过半径外端并且垂直于这条半径的直线是圆的切线
切线的性质 1.切线与圆只有一个公共点. 2.切线到圆心的距离等于圆的⑤ . 3.切线垂直于经过切点的半径
切线长 1.定义:从圆外一点作圆的切线,这点与切点之间的线段长叫作这点到圆的切线长. 2.切线长定理:从圆外一点可以引圆的两条切线,两切线长⑥ ,圆心与这一点的连线平分两条切线的夹角
考点3三角形与圆 (轮考点)
三角形的 外接圆 图形 相关概念 圆心的确定 内、外心的性质
经过三角形各顶点的圆叫作三角形的外接圆,外接圆的圆心叫作三角形的外心,这个三角形叫作圆的内接三角形 三角形三边垂直平分线的交点 外心到三角形的三个⑦ 的距离相等
三角形的 内切圆 与三角形各边都相切的圆叫作三角形的内切圆,内切圆的圆心叫作三角形的内心 三角形三条角平分线的交点 内心到三角形的三条边的距离相等
【温馨提示】1.在△ABC中,若∠ACB=90°,AC=b,BC=a,AB=c,则△ABC内切圆的半径r= 2.△ABC的三边长分别为a,b,c,☉O内切于△ABC,且半径为r,则有r=
【基础演练】
1.(人教九上P101第1题变式)已知☉O的半径为3 cm,点P到圆心O的距离OP=2 cm,则点P ( )
A.在☉O外 B.在☉O上
C.在☉O内 D.无法确定
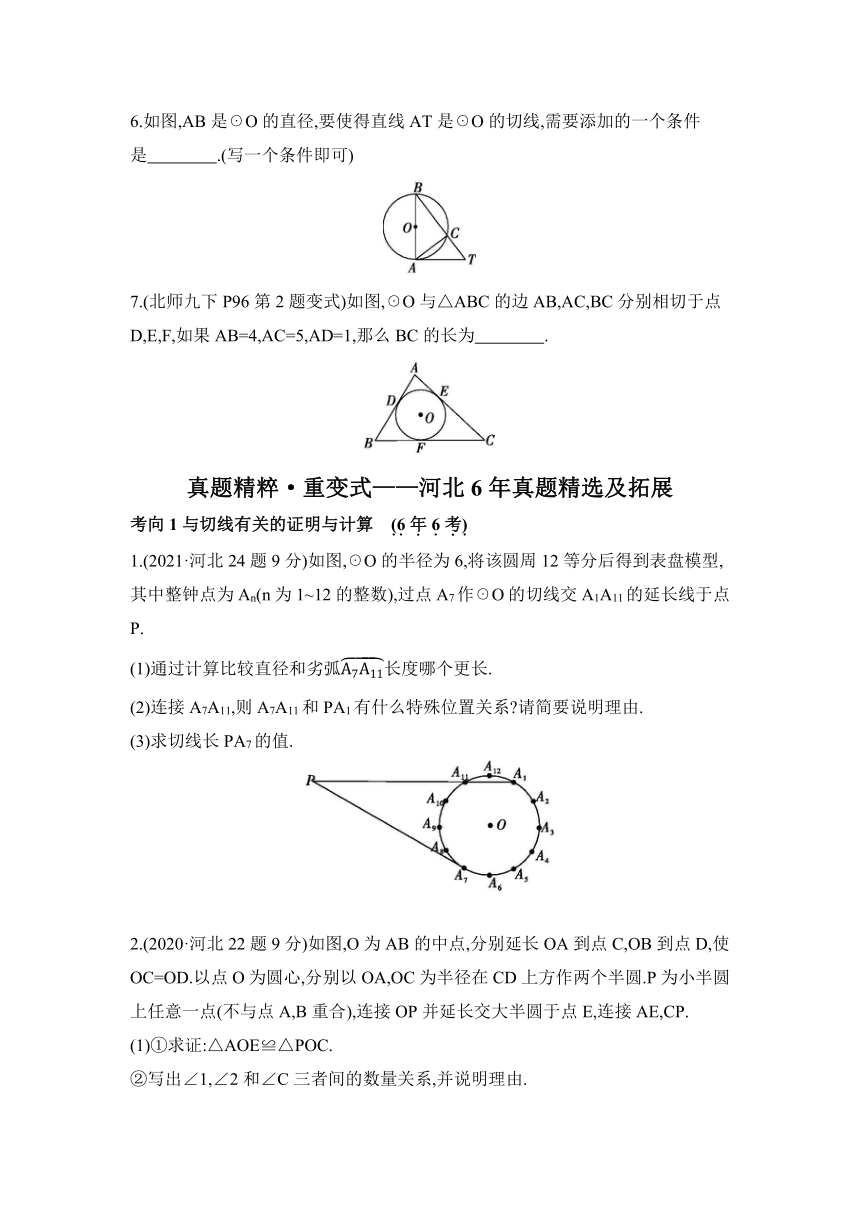
2.如图,在4×4的网格图中,A,B,C是三个格点,其中每个小正方形的边长为1,△ABC的外心可能是( )
A.M点 B.N点
C.P点 D.Q点
3.(冀教九下P9第1题变式)如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为 ( )
A.3
B.3
C.6
D.9
4.(冀教九下P7第2题变式)在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆 ( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
5.(北师九下P93习题3.8第2题改编)如图,I是△ABC的内心,若∠AIB=125°,则∠C等于 ( )
A.65° B.70°
C.75° D.80°
6.如图,AB是☉O的直径,要使得直线AT是☉O的切线,需要添加的一个条件是 .(写一个条件即可)
7.(北师九下P96第2题变式)如图,☉O与△ABC的边AB,AC,BC分别相切于点D,E,F,如果AB=4,AC=5,AD=1,那么BC的长为 .
真题精粹·重变式——河北6年真题精选及拓展
考向1与切线有关的证明与计算 (6年6考)
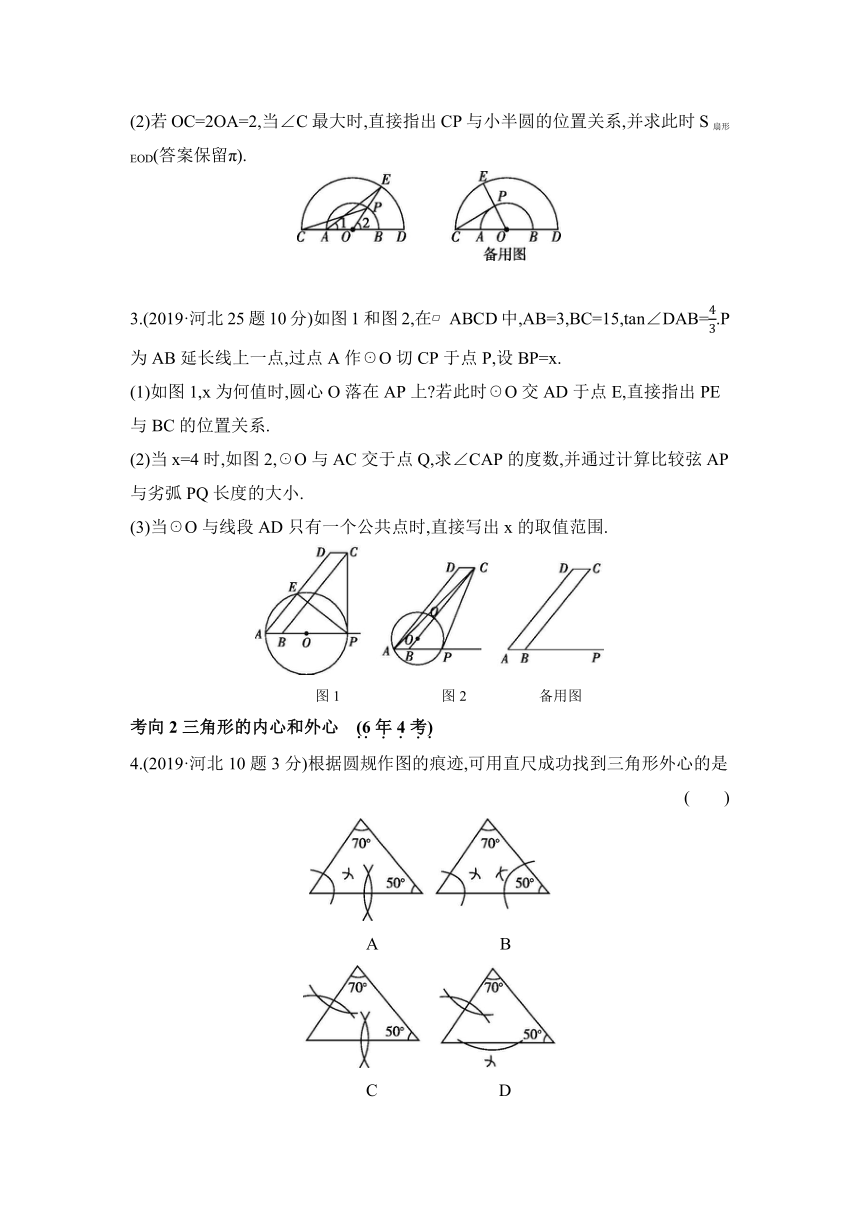
1.(2021·河北24题9分)如图,☉O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作☉O的切线交A1A11的延长线于点P.
(1)通过计算比较直径和劣弧长度哪个更长.
(2)连接A7A11,则A7A11和PA1有什么特殊位置关系 请简要说明理由.
(3)求切线长PA7的值.
2.(2020·河北22题9分)如图,O为AB的中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.P为小半圆上任意一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.
(1)①求证:△AOE≌△POC.
②写出∠1,∠2和∠C三者间的数量关系,并说明理由.
(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).
3.(2019·河北25题10分)如图1和图2,在 ABCD中,AB=3,BC=15,tan∠DAB=.P为AB延长线上一点,过点A作☉O切CP于点P,设BP=x.
(1)如图1,x为何值时,圆心O落在AP上 若此时☉O交AD于点E,直接指出PE与BC的位置关系.
(2)当x=4时,如图2,☉O与AC交于点Q,求∠CAP的度数,并通过计算比较弦AP与劣弧PQ长度的大小.
(3)当☉O与线段AD只有一个公共点时,直接写出x的取值范围.
图1 图2 备用图
考向2三角形的内心和外心 (6年4考)
4.(2019·河北10题3分)根据圆规作图的痕迹,可用直尺成功找到三角形外心的是 ( )
A B
C D
5.(2020·河北14题2分)有一题目:“已知点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为画△ABC以及它的外接圆O,连接OB,OC,如图所示.由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是 ( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
6.(2022·河北16题2分)题目:“如图,∠B=45°,BC=2,在射线BM上取一点A,设AC=d,若对于d的一个数值,只能作出唯一一个△ABC,求d的取值范围.”对于其答案,甲答:d≥2.乙答:d=1.6.丙答:d=.则正确的是 ( )
A.只有甲答得对
B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整
D.三人答案合在一起才完整
核心突破·拓思维——学科核心素养提升
题型1 与切线有关的证明与计算
(原创·一题多设问)如图1,已知AB是☉O的直径,P为BA延长线上一点,PC是☉O的切线,C为切点,连接BC.
(1)若∠P=26°,则∠B的度数为 °.
(2)若☉O 的直径等于5, PC=6,则PA= .
(3)若CP=CB,①则∠B的度数为 ;②当PA=3时,PC= .
(4)如图2,过点A作☉O的切线交CP于点E,若CP=8,AE=3,则△APE的周长为 ,☉O的半径为 .
(5)如图3,过点B作BD⊥PC交PC的延长线于点D.
①求证:BC平分∠PBD.
②若BC=2,BD=3,求☉O的直径AB的长.
“切线的故事”
1个主题 直角三角形
4条线索 勾股定理
三角函数
相似
面积法
圆的切线是河北省中考必考知识点,并且所占分量较重,有时在一份试卷的不同题型中两次考查.其中,切线相关性质(包括切线长定理等)重点考查,切线的判定考查较少.因为圆的知识综合性较强,所以在解答题中必然与其他几何知识融为一体,有时甚至占据压轴题的位置,难度相对较大.
1.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为 ( )
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
2.(中华优秀传统文化)在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1所示,两个固定长度的“连杆”AP,BP的连接点P在☉O上,当点P在☉O上转动时,带动点A,B分别在射线OM,ON上滑动,OM⊥ON.当AP与☉O相切时,点B恰好落在☉O上,如图2所示.请仅就图2的情形解答下列问题.
(1)求证:∠PAO=2∠PBO.
(2)若☉O的半径为3,AP=4,求BP的长.
1.一条切线时,可用切线的性质定理.
2.两条切线时,若两条切线相交,则可用切线长定理;若两条切线平行,则两条切线间的距离等于圆的直径.
3.三条切线时,围成的三角形是圆的外切三角形.
4.四条切线时,围成的四边形是圆的外切四边形,两组对边的和相等.
5.更多切线时,围成的多边形是圆的外切多边形,若多边形是正多边形,则可利用圆的有关计算方法解决正多边形问题.
(1)由切线的性质,得到直角三角形锐角互余
↓
利用圆周角与圆心角的关系进行证明
↓
(2)过点P作PD⊥BC于点D,结合(1)证明△PDO∽△OPA
↓
由对应边成比例,求出PD,OD
↓
在Rt△PBD中运用勾股定理求PB的长
题型2 与内心或外心相关的计算
(2024·邯郸模拟)如图1,把△ABC剪成三部分,边AB,BC,AC放在同一直线l上(如图2),点O都落在直线MN上,直线MN∥l.在△ABC中,若∠BOC=125°,则∠BAC的度数为 ( )
图1
图2
A.60° B.65° C.70° D.75°
利用内心横向拓展,串联相关知识
·角平分线(出现相等的角)
·角平分线的性质(出现相等的垂线段)
·全等三角形(出现更多相等的角与相等的线段)
·“内心角”与内角关系∠BIC=90°+
·过内心作一边的平行线→两个等腰三角形→截得三角形的周长=另两边之和
·到三边距离相等均为内切圆半径r,S△ABC=,l=a+b+c
·m=,n=,p=
如图,在△ABC中,AC=8,∠A=30°,∠CBA=50°,P为AB边上任意一点(P不与点B,A重合),I为△BPC的内心,则
(1)CP的最小值为 .
(2)∠CIB的取值范围是 .
三角形的内心与外心曾是河北省中考试卷上的“常客”,不仅会在选择、填空题中单独考查,也会与三角形、四边形等知识综合考查,并且在解答题中经常作为难度较大的题目出现.虽然近两年辉煌不再,但仍值得重视,有时会“改头换面”出现在试卷中.
(1)由“垂线段最短”构造直角三角形,利用含有30°角的直角三角形性质求解.
(2)由角平分线定义和三角形内角和定理,可得∠CIB=90°+∠BPC,故∠CIB的大小取决于∠BPC.由P为AB边上任意一点(P不与点B,A重合)可知,30°<∠BPC<130°,据此计算∠CIB的取值范围.
参考答案
考点清单
①< ②= ③> ④半径 ⑤半径 ⑥相等 ⑦顶点
基础演练
1.C 2.D 3.C 4.A 5.B
6.∠TAC=∠B(答案不唯一) 7.7
真题精粹·重变式
1.(1)劣弧=×2π×6=4π>12,
∴劣弧比直径长.
(2)PA1⊥A7A11.理由:如图,连接A1A7.
∵A1A7是☉O的直径,
∴∠A7A11A1=90°,
∴PA1⊥A7A11.
(3)∵PA7是☉O的切线,
∴PA7⊥A1A7,
∴∠PA7A1=90°.
∵∠PA1A7=60°,A1A7=12,
∴PA7=A1A7·tan 60°=12.
2.(1)①证明:在△AOE和△POC中,
∴△AOE≌△POC(SAS).
②∠1+∠C=∠2.
理由:∵△AOE≌△POC,∴∠E=∠C.
∵∠1+∠E=∠2,∴∠1+∠C=∠2.
(2)当CP与小半圆相切时,∠C最大.
∵OC=2OA=2,∴OC=2OP.
∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,
∴S扇形EOD==π.
3.(1)∵CP与☉O相切于点P,∴∠APC=90°.
∵四边形ABCD为平行四边形,∴AD∥BC,
∴∠PBC=∠DAB,
∴=tan∠PBC=tan∠DAB=.
设CP=4k,BP=3k,由CP2+BP2=BC2,
得(4k)2+(3k)2=152,解得k1=-3(舍去),k2=3,
∴x=BP=3×3=9,
故当x=9时,圆心O落在AP上.
∵AP是☉O的直径,∴∠AEP=90°,∴PE⊥AD.
∵四边形ABCD为平行四边形,∴BC∥AD,
∴PE⊥BC.
(2)如图1,过点C作CG⊥AP于点G.
∵四边形ABCD为平行四边形,∴BC∥AD,
∴∠CBG=∠DAB,
∴=tan∠CBG=tan∠DAB=.
设CG=4m,BG=3m,由勾股定理得(4m)2+(3m)2=152,解得m=3,
∴CG=4×3=12,BG=3×3=9,PG=BG-BP=9-4=5,AP=AB+BP=3+4=7,
∴AG=AB+BG=3+9=12,
∴tan∠CAP===1,∴∠CAP=45°.
连接OP,OQ,过点O作OH⊥AP于点H,则∠POQ=2∠CAP=2×45°=90°,PH=AP=.
在Rt△CPG中,CP===13.
∵CP是☉O的切线,∴∠OPC=∠OHP=90°,∠OPH+∠CPG=90°,∠PCG+∠CPG=90°,
∴∠OPH=∠PCG,∴△OPH∽△PCG,
∴=,即PH×CP=CG×OP,×13=12OP,∴OP=,
∴劣弧PQ的长度==π.
∵π<2π<7,
∴弦AP的长度>劣弧PQ的长度.
(3)如图2,☉O与线段AD只有一个公共点,即圆心O位于直线AB下方,且∠OAD≥90°.
当∠OAD=90°,∠CPM=∠DAB时,此时BP取得最小值,过点C作CM⊥AB于点M.
∵∠DAB=∠CBP,
∴∠CPM=∠CBP,
∴CB=CP.
∵CM⊥AB,∴BP=2BM=2×9=18,∴x≥18.
4.C 5.A 6.B
核心突破·拓思维
例1
(1)32. (2)4. (3)30°;3. (4)12;6.
(5) ①证明:如图,连接OC.
∵PC与☉O相切,
∴OC⊥PC,即∠OCP=90°.∵BD⊥PD,
∴∠BDP=90°,
∴OC∥BD,
∴∠BCO=∠CBD.
∵OB=OC,∴∠PBC=∠BCO,∴∠PBC=∠CBD,
∴BC平分∠PBD;
②如图,连接AC.
∵AB为☉O的直径,∴∠ACB=90°,
∴∠ACB=∠CDB=90°.∵∠ABC=∠CBD,
∴△ABC∽△CBD,∴BC∶BD= AB∶BC,
∴BC2=AB·BD,即(2)2=AB×3,∴AB=4.
变式训练
1.B 提示:如图,设D,E,F分别是☉O的切点,则DM=MF,FN=EN.
∵AB+BC+AC=17 cm,BC=5 cm,
由切线长定理,得BD+CE=BC=5 cm,
∴AD+AE=17-2×5=7(cm),
∴AM+AN+MN=AD+AE=7(cm),故选B.
2.(1)证明:如图1,连接OP.
∵AP与☉O相切,
∴OP⊥AP,
∴∠APO=90°,
∴∠PAO+∠POA=90°,OM⊥ON,
∴∠POQ+∠POA=90°,
∴∠POQ=∠PAO.
∵点B恰好落在☉O上,
∴∠PBO=∠POQ=∠PAO,
∴∠PAO=2∠PBO.
(2)如图2,连接CP,过点P作PD⊥BC于点D,∠PDO=90°,
由(1)可知,∠POQ=∠PAO,∠APO=90°,
∴△PDO∽△OPA,
∴==.
∵AO2=AP2+OP2,☉O的半径为3,AP=4,
∴AO=5,∴==,∴PD=,OD=,
∴BD=BO+OD=3+=.
在Rt△PBD中,PB2=PD2+BD2,
∴PB2=2+2,∴PB=.
例2
C 提示:如图,过点O分别作OD⊥AC于点D,OE⊥AB于点E,OF⊥BC于点F.
∵直线MN∥l,
∴OD=OE=OF,
∴点O是△ABC的内心,O为三个内角平分线的交点,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2×(180°-125°)=110°,
∴∠BAC=70°,故选C.
变式训练
(1)4 (2)105°<∠CIB<155°
提示:(1)根据垂线段最短可知,当CP⊥AB时,PC的值最小.
∵此时∠APC=90°,∠A=30°,
∴PC=AC=4.
故答案为4.
(2)∵I为△BPC的内心,
∴∠IBC=∠PBC,∠ICB=∠PCB,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-(∠PBC+∠PCB)=180°-(180°-∠BPC)=90°+∠BPC.
∵30°<∠BPC<130°,
∴105°<∠BIC<155°.
故答案为105°<∠BIC<155°.
(6年10考,2~10分)
与圆有关的位置关系涉及的知识点很多,其中切线的性质是重中之重.预测2025年中考的解答题中,仍会考查切线的性质,并与其他几何知识组合成为圆的综合题,而且考查难度增大.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1与圆有关的位置关系
点与圆的 位置关系 设点到圆心的距离为d 1.d① r 点在☉O内. 2.d② r 点在☉O上. 3.d③ r 点在☉O外
直线与 圆的位 置关系 位置关系 相离 相切 相交
图形
公共点个数 0 1 2
数量关系 d>r d=r d
切线的判定 1.与圆只有一个公共点的直线是圆的切线(定义法). 2.到圆心的距离等于④ 的直线是圆的切线. 3.经过半径外端并且垂直于这条半径的直线是圆的切线
切线的性质 1.切线与圆只有一个公共点. 2.切线到圆心的距离等于圆的⑤ . 3.切线垂直于经过切点的半径
切线长 1.定义:从圆外一点作圆的切线,这点与切点之间的线段长叫作这点到圆的切线长. 2.切线长定理:从圆外一点可以引圆的两条切线,两切线长⑥ ,圆心与这一点的连线平分两条切线的夹角
考点3三角形与圆 (轮考点)
三角形的 外接圆 图形 相关概念 圆心的确定 内、外心的性质
经过三角形各顶点的圆叫作三角形的外接圆,外接圆的圆心叫作三角形的外心,这个三角形叫作圆的内接三角形 三角形三边垂直平分线的交点 外心到三角形的三个⑦ 的距离相等
三角形的 内切圆 与三角形各边都相切的圆叫作三角形的内切圆,内切圆的圆心叫作三角形的内心 三角形三条角平分线的交点 内心到三角形的三条边的距离相等
【温馨提示】1.在△ABC中,若∠ACB=90°,AC=b,BC=a,AB=c,则△ABC内切圆的半径r= 2.△ABC的三边长分别为a,b,c,☉O内切于△ABC,且半径为r,则有r=
【基础演练】
1.(人教九上P101第1题变式)已知☉O的半径为3 cm,点P到圆心O的距离OP=2 cm,则点P ( )
A.在☉O外 B.在☉O上
C.在☉O内 D.无法确定
2.如图,在4×4的网格图中,A,B,C是三个格点,其中每个小正方形的边长为1,△ABC的外心可能是( )
A.M点 B.N点
C.P点 D.Q点
3.(冀教九下P9第1题变式)如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为 ( )
A.3
B.3
C.6
D.9
4.(冀教九下P7第2题变式)在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆 ( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
5.(北师九下P93习题3.8第2题改编)如图,I是△ABC的内心,若∠AIB=125°,则∠C等于 ( )
A.65° B.70°
C.75° D.80°
6.如图,AB是☉O的直径,要使得直线AT是☉O的切线,需要添加的一个条件是 .(写一个条件即可)
7.(北师九下P96第2题变式)如图,☉O与△ABC的边AB,AC,BC分别相切于点D,E,F,如果AB=4,AC=5,AD=1,那么BC的长为 .
真题精粹·重变式——河北6年真题精选及拓展
考向1与切线有关的证明与计算 (6年6考)
1.(2021·河北24题9分)如图,☉O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作☉O的切线交A1A11的延长线于点P.
(1)通过计算比较直径和劣弧长度哪个更长.
(2)连接A7A11,则A7A11和PA1有什么特殊位置关系 请简要说明理由.
(3)求切线长PA7的值.
2.(2020·河北22题9分)如图,O为AB的中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.P为小半圆上任意一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.
(1)①求证:△AOE≌△POC.
②写出∠1,∠2和∠C三者间的数量关系,并说明理由.
(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).
3.(2019·河北25题10分)如图1和图2,在 ABCD中,AB=3,BC=15,tan∠DAB=.P为AB延长线上一点,过点A作☉O切CP于点P,设BP=x.
(1)如图1,x为何值时,圆心O落在AP上 若此时☉O交AD于点E,直接指出PE与BC的位置关系.
(2)当x=4时,如图2,☉O与AC交于点Q,求∠CAP的度数,并通过计算比较弦AP与劣弧PQ长度的大小.
(3)当☉O与线段AD只有一个公共点时,直接写出x的取值范围.
图1 图2 备用图
考向2三角形的内心和外心 (6年4考)
4.(2019·河北10题3分)根据圆规作图的痕迹,可用直尺成功找到三角形外心的是 ( )
A B
C D
5.(2020·河北14题2分)有一题目:“已知点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为画△ABC以及它的外接圆O,连接OB,OC,如图所示.由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是 ( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同值
6.(2022·河北16题2分)题目:“如图,∠B=45°,BC=2,在射线BM上取一点A,设AC=d,若对于d的一个数值,只能作出唯一一个△ABC,求d的取值范围.”对于其答案,甲答:d≥2.乙答:d=1.6.丙答:d=.则正确的是 ( )
A.只有甲答得对
B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整
D.三人答案合在一起才完整
核心突破·拓思维——学科核心素养提升
题型1 与切线有关的证明与计算
(原创·一题多设问)如图1,已知AB是☉O的直径,P为BA延长线上一点,PC是☉O的切线,C为切点,连接BC.
(1)若∠P=26°,则∠B的度数为 °.
(2)若☉O 的直径等于5, PC=6,则PA= .
(3)若CP=CB,①则∠B的度数为 ;②当PA=3时,PC= .
(4)如图2,过点A作☉O的切线交CP于点E,若CP=8,AE=3,则△APE的周长为 ,☉O的半径为 .
(5)如图3,过点B作BD⊥PC交PC的延长线于点D.
①求证:BC平分∠PBD.
②若BC=2,BD=3,求☉O的直径AB的长.
“切线的故事”
1个主题 直角三角形
4条线索 勾股定理
三角函数
相似
面积法
圆的切线是河北省中考必考知识点,并且所占分量较重,有时在一份试卷的不同题型中两次考查.其中,切线相关性质(包括切线长定理等)重点考查,切线的判定考查较少.因为圆的知识综合性较强,所以在解答题中必然与其他几何知识融为一体,有时甚至占据压轴题的位置,难度相对较大.
1.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为 ( )
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
2.(中华优秀传统文化)在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1所示,两个固定长度的“连杆”AP,BP的连接点P在☉O上,当点P在☉O上转动时,带动点A,B分别在射线OM,ON上滑动,OM⊥ON.当AP与☉O相切时,点B恰好落在☉O上,如图2所示.请仅就图2的情形解答下列问题.
(1)求证:∠PAO=2∠PBO.
(2)若☉O的半径为3,AP=4,求BP的长.
1.一条切线时,可用切线的性质定理.
2.两条切线时,若两条切线相交,则可用切线长定理;若两条切线平行,则两条切线间的距离等于圆的直径.
3.三条切线时,围成的三角形是圆的外切三角形.
4.四条切线时,围成的四边形是圆的外切四边形,两组对边的和相等.
5.更多切线时,围成的多边形是圆的外切多边形,若多边形是正多边形,则可利用圆的有关计算方法解决正多边形问题.
(1)由切线的性质,得到直角三角形锐角互余
↓
利用圆周角与圆心角的关系进行证明
↓
(2)过点P作PD⊥BC于点D,结合(1)证明△PDO∽△OPA
↓
由对应边成比例,求出PD,OD
↓
在Rt△PBD中运用勾股定理求PB的长
题型2 与内心或外心相关的计算
(2024·邯郸模拟)如图1,把△ABC剪成三部分,边AB,BC,AC放在同一直线l上(如图2),点O都落在直线MN上,直线MN∥l.在△ABC中,若∠BOC=125°,则∠BAC的度数为 ( )
图1
图2
A.60° B.65° C.70° D.75°
利用内心横向拓展,串联相关知识
·角平分线(出现相等的角)
·角平分线的性质(出现相等的垂线段)
·全等三角形(出现更多相等的角与相等的线段)
·“内心角”与内角关系∠BIC=90°+
·过内心作一边的平行线→两个等腰三角形→截得三角形的周长=另两边之和
·到三边距离相等均为内切圆半径r,S△ABC=,l=a+b+c
·m=,n=,p=
如图,在△ABC中,AC=8,∠A=30°,∠CBA=50°,P为AB边上任意一点(P不与点B,A重合),I为△BPC的内心,则
(1)CP的最小值为 .
(2)∠CIB的取值范围是 .
三角形的内心与外心曾是河北省中考试卷上的“常客”,不仅会在选择、填空题中单独考查,也会与三角形、四边形等知识综合考查,并且在解答题中经常作为难度较大的题目出现.虽然近两年辉煌不再,但仍值得重视,有时会“改头换面”出现在试卷中.
(1)由“垂线段最短”构造直角三角形,利用含有30°角的直角三角形性质求解.
(2)由角平分线定义和三角形内角和定理,可得∠CIB=90°+∠BPC,故∠CIB的大小取决于∠BPC.由P为AB边上任意一点(P不与点B,A重合)可知,30°<∠BPC<130°,据此计算∠CIB的取值范围.
参考答案
考点清单
①< ②= ③> ④半径 ⑤半径 ⑥相等 ⑦顶点
基础演练
1.C 2.D 3.C 4.A 5.B
6.∠TAC=∠B(答案不唯一) 7.7
真题精粹·重变式
1.(1)劣弧=×2π×6=4π>12,
∴劣弧比直径长.
(2)PA1⊥A7A11.理由:如图,连接A1A7.
∵A1A7是☉O的直径,
∴∠A7A11A1=90°,
∴PA1⊥A7A11.
(3)∵PA7是☉O的切线,
∴PA7⊥A1A7,
∴∠PA7A1=90°.
∵∠PA1A7=60°,A1A7=12,
∴PA7=A1A7·tan 60°=12.
2.(1)①证明:在△AOE和△POC中,
∴△AOE≌△POC(SAS).
②∠1+∠C=∠2.
理由:∵△AOE≌△POC,∴∠E=∠C.
∵∠1+∠E=∠2,∴∠1+∠C=∠2.
(2)当CP与小半圆相切时,∠C最大.
∵OC=2OA=2,∴OC=2OP.
∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,
∴S扇形EOD==π.
3.(1)∵CP与☉O相切于点P,∴∠APC=90°.
∵四边形ABCD为平行四边形,∴AD∥BC,
∴∠PBC=∠DAB,
∴=tan∠PBC=tan∠DAB=.
设CP=4k,BP=3k,由CP2+BP2=BC2,
得(4k)2+(3k)2=152,解得k1=-3(舍去),k2=3,
∴x=BP=3×3=9,
故当x=9时,圆心O落在AP上.
∵AP是☉O的直径,∴∠AEP=90°,∴PE⊥AD.
∵四边形ABCD为平行四边形,∴BC∥AD,
∴PE⊥BC.
(2)如图1,过点C作CG⊥AP于点G.
∵四边形ABCD为平行四边形,∴BC∥AD,
∴∠CBG=∠DAB,
∴=tan∠CBG=tan∠DAB=.
设CG=4m,BG=3m,由勾股定理得(4m)2+(3m)2=152,解得m=3,
∴CG=4×3=12,BG=3×3=9,PG=BG-BP=9-4=5,AP=AB+BP=3+4=7,
∴AG=AB+BG=3+9=12,
∴tan∠CAP===1,∴∠CAP=45°.
连接OP,OQ,过点O作OH⊥AP于点H,则∠POQ=2∠CAP=2×45°=90°,PH=AP=.
在Rt△CPG中,CP===13.
∵CP是☉O的切线,∴∠OPC=∠OHP=90°,∠OPH+∠CPG=90°,∠PCG+∠CPG=90°,
∴∠OPH=∠PCG,∴△OPH∽△PCG,
∴=,即PH×CP=CG×OP,×13=12OP,∴OP=,
∴劣弧PQ的长度==π.
∵π<2π<7,
∴弦AP的长度>劣弧PQ的长度.
(3)如图2,☉O与线段AD只有一个公共点,即圆心O位于直线AB下方,且∠OAD≥90°.
当∠OAD=90°,∠CPM=∠DAB时,此时BP取得最小值,过点C作CM⊥AB于点M.
∵∠DAB=∠CBP,
∴∠CPM=∠CBP,
∴CB=CP.
∵CM⊥AB,∴BP=2BM=2×9=18,∴x≥18.
4.C 5.A 6.B
核心突破·拓思维
例1
(1)32. (2)4. (3)30°;3. (4)12;6.
(5) ①证明:如图,连接OC.
∵PC与☉O相切,
∴OC⊥PC,即∠OCP=90°.∵BD⊥PD,
∴∠BDP=90°,
∴OC∥BD,
∴∠BCO=∠CBD.
∵OB=OC,∴∠PBC=∠BCO,∴∠PBC=∠CBD,
∴BC平分∠PBD;
②如图,连接AC.
∵AB为☉O的直径,∴∠ACB=90°,
∴∠ACB=∠CDB=90°.∵∠ABC=∠CBD,
∴△ABC∽△CBD,∴BC∶BD= AB∶BC,
∴BC2=AB·BD,即(2)2=AB×3,∴AB=4.
变式训练
1.B 提示:如图,设D,E,F分别是☉O的切点,则DM=MF,FN=EN.
∵AB+BC+AC=17 cm,BC=5 cm,
由切线长定理,得BD+CE=BC=5 cm,
∴AD+AE=17-2×5=7(cm),
∴AM+AN+MN=AD+AE=7(cm),故选B.
2.(1)证明:如图1,连接OP.
∵AP与☉O相切,
∴OP⊥AP,
∴∠APO=90°,
∴∠PAO+∠POA=90°,OM⊥ON,
∴∠POQ+∠POA=90°,
∴∠POQ=∠PAO.
∵点B恰好落在☉O上,
∴∠PBO=∠POQ=∠PAO,
∴∠PAO=2∠PBO.
(2)如图2,连接CP,过点P作PD⊥BC于点D,∠PDO=90°,
由(1)可知,∠POQ=∠PAO,∠APO=90°,
∴△PDO∽△OPA,
∴==.
∵AO2=AP2+OP2,☉O的半径为3,AP=4,
∴AO=5,∴==,∴PD=,OD=,
∴BD=BO+OD=3+=.
在Rt△PBD中,PB2=PD2+BD2,
∴PB2=2+2,∴PB=.
例2
C 提示:如图,过点O分别作OD⊥AC于点D,OE⊥AB于点E,OF⊥BC于点F.
∵直线MN∥l,
∴OD=OE=OF,
∴点O是△ABC的内心,O为三个内角平分线的交点,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2×(180°-125°)=110°,
∴∠BAC=70°,故选C.
变式训练
(1)4 (2)105°<∠CIB<155°
提示:(1)根据垂线段最短可知,当CP⊥AB时,PC的值最小.
∵此时∠APC=90°,∠A=30°,
∴PC=AC=4.
故答案为4.
(2)∵I为△BPC的内心,
∴∠IBC=∠PBC,∠ICB=∠PCB,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-(∠PBC+∠PCB)=180°-(180°-∠BPC)=90°+∠BPC.
∵30°<∠BPC<130°,
∴105°<∠BIC<155°.
故答案为105°<∠BIC<155°.
同课章节目录
