【中考考点探究】第3节 一次函数的实际应用 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第3节 一次函数的实际应用 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 193.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:42:44 | ||
图片预览


文档简介
第3节 一次函数的实际应用
(6年2考,9~10分)
一次函数与二次函数一共占据2道解答题,通常其中一道考查图象性质,另一道考查实际应用.近年来,一次函数的实际应用问题以图象型居多,但2024年发生改变,以文字为主阐述现实情境,通过变量关系列一次函数解决实际问题,并且与统计实现跨领域结合.这意味着2025年对一次函数实际应用的考查类型不确定性变大,综合性增强.
真题精粹·重变式——河北6年真题精选及拓展
考向1图象型一次函数应用问题 (6年1考)
1.(2023·河北23题9分)如图,这是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3km/min的速度在离地面5km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿45°仰角爬升,到4km高的A处便立刻转为水平飞行,再过1 min到达B处开始沿直线BC降落,要求1 min 后到达C(10,3)处.
(1)求OA的h关于s的函数解析式,并直接写出2号机的爬升速度.
(2)求BC的h关于s的函数解析式,并预计2号机着陆点的坐标.
(3)通过计算求出两机距离PQ不超过3km的时长.
(注:(1)及(2)中不必写s的取值范围)
考向2文字、表格型一次函数应用问题 (6年1考)
2.(2024·河北24题10分)长为300 m的春游队伍,以v(单位:m/s)的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(单位:m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(单位:s),排头与O的距离为S头(单位:m).
图1 图2
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(单位:m),求S甲与t的函数关系式(不写t的取值范围).
(2)设甲这次往返队伍的总时间为T(单位:s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
核心突破·拓思维——学科核心素养提升
题型1 图象型一次函数应用问题
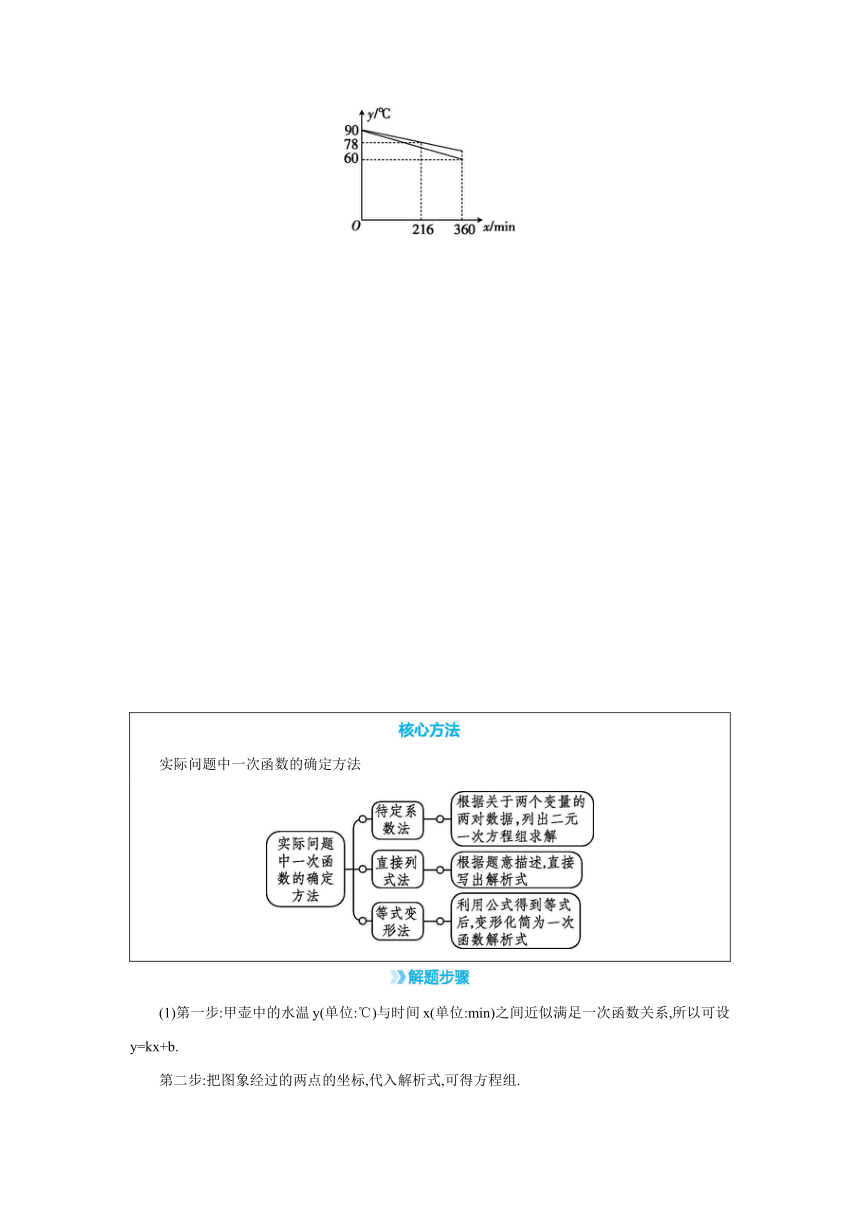
小明和爸爸各买了一个保温壶,分别记为甲和乙.小明对这两个保温壶进行了保温测试,在其中同时分别倒入同样多90 ℃的热水,经过一段时间的测试发现,乙的保温性能好且这段时间内,甲、乙保温壶中的水温y(单位:℃)与时间x(单位:min)之间都近似满足一次函数关系如图所示.根据相关信息,解答下列问题:
(1)求甲壶中的水温y与x的函数关系式(不必写自变量的取值范围).
(2)当乙壶中的水温是78 ℃时,甲壶中水的温度是多少
(3)测试多长时间内,这两个保温壶中水的温差不超过5 ℃
实际问题中一次函数的确定方法
(1)第一步:甲壶中的水温y(单位:℃)与时间x(单位:min)之间近似满足一次函数关系,所以可设y=kx+b.
第二步:把图象经过的两点的坐标,代入解析式,可得方程组.
第三步:解方程组得到k与b的值,从而求得函数解析式.
以上求函数解析式所用的数学方法是待定系数法.
(2)第一步:观察图象可知,当乙壶中的水温是78 ℃时,x对应的值.
第二步:将x的值代入(1)中求得的解析式,计算得到甲壶中水的温度.
(3)第一步:同(1)求得乙壶中的水温y与x的函数关系式.
第二步:根据“两个保温壶的温差不超过5 ℃”列不等式.
第三步:解不等式,得到答案
题型2 文字、表格型实际应用问题
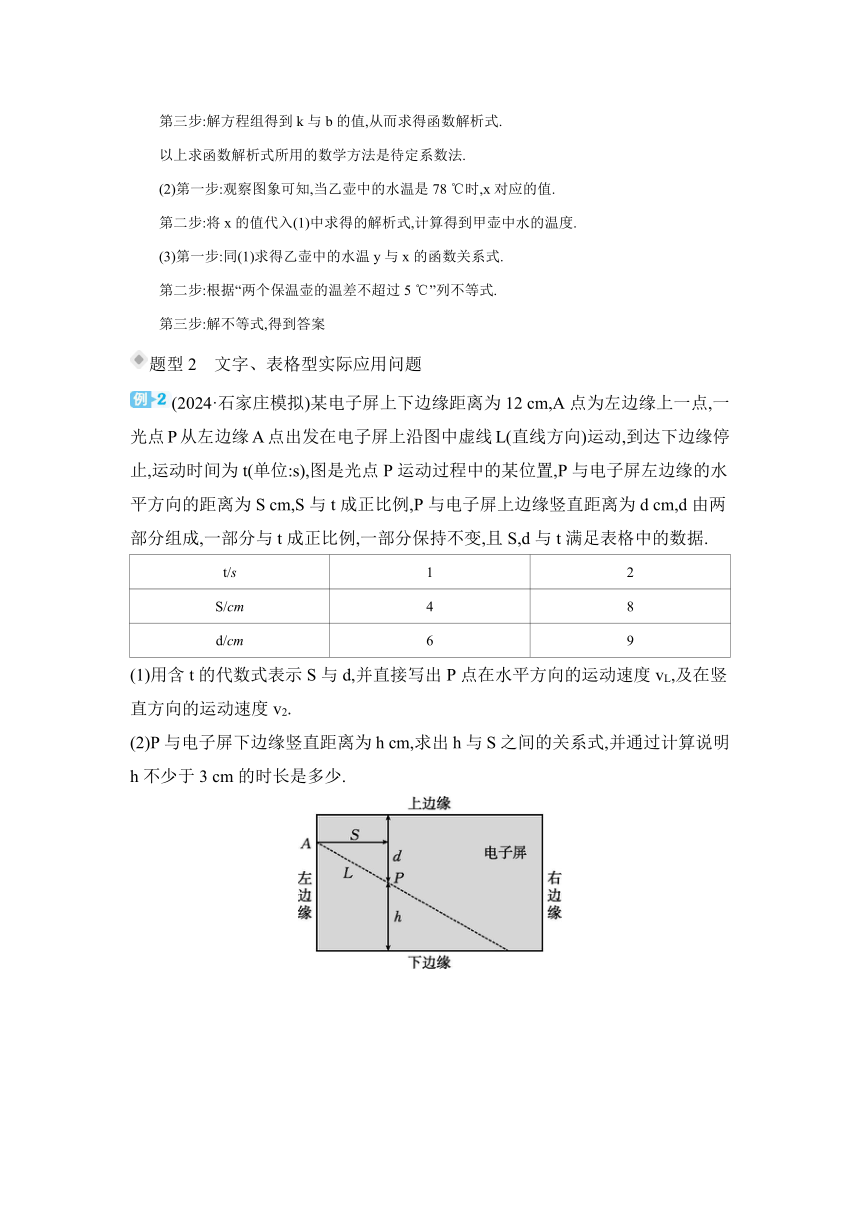
(2024·石家庄模拟)某电子屏上下边缘距离为12 cm,A点为左边缘上一点,一光点P从左边缘A点出发在电子屏上沿图中虚线L(直线方向)运动,到达下边缘停止,运动时间为t(单位:s),图是光点P运动过程中的某位置,P与电子屏左边缘的水平方向的距离为S cm,S与t成正比例,P与电子屏上边缘竖直距离为d cm,d由两部分组成,一部分与t成正比例,一部分保持不变,且S,d与t满足表格中的数据.
t/s 1 2
S/cm 4 8
d/cm 6 9
(1)用含t的代数式表示S与d,并直接写出P点在水平方向的运动速度vL,及在竖直方向的运动速度v2.
(2)P与电子屏下边缘竖直距离为h cm,求出h与S之间的关系式,并通过计算说明h不少于3 cm的时长是多少.
解一次函数实际应用问题的一般方法
河北省考查一次函数的实际应用问题,通常会涉及23个函数关系式,通过它们之间的联系与差异作为命题点,与方程、不等式相结合.有时会借助表格、图画、图形、光点运动等表达方式,丰富情境素材.
参考答案
真题精粹·重变式
1.(1)∵2号机爬升角度为45°,
∴OA上的点的横纵坐标相同,
∴A(4,4).
设OA的解析式为h=ks,
∴4k=4,
∴k=1,
∴OA的解析式为h=s.
∵2号机一直保持在1号机的正下方,
∴它们飞行的时间和飞行的水平距离相同.
∵2号机爬升到A处时水平方向上移动了4km,飞行的距离为4km,
又∵1号机的飞行速度为3km/min,
∴2号机的爬升速度为4÷=3 km/min.
(2)设BC的解析式为h=ms+n.
由题意得B(7,4),C(10,3),
∴解得
∴BC的解析式为h=-s+.
令h=0,则s=19.
∴预计2号机着陆点的坐标为(19,0).
(3)当PQ=3km时,h=5-3=2(km).
由h=s,得s=2;
由-s+=2,得s=13.
∴两机距离PQ不超过3km的时长为(13-2)÷3=(min).
2.(1)①排尾从位置O开始行进的时间为t (s),则排头也离开原排头t (s),
∴S头=2t+300.
②甲从排尾赶到排头的时间为300÷(2v-v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m.
甲返回时间为(t-150)s,
∴S甲=600-S甲回=600-4(t-150)=1 200-4t;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S头的值为600 m,在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=1 200-4t.
(2)T=t追及+t返回=+=,
在甲这次往返队伍的过程中队伍行进的路程为v×=400 m.
因此T与v的函数关系式为T=,此时队伍在此过程中行进的路程为400 m.
核心突破·拓思维
例1
(1)设甲壶中的水温y与x的函数关系式为y=kx+b.
∵乙壶的保温性能好,
∴甲壶的水温y与时间x的关系图象经过点(0,90),(360,60).
分别代入,得解得
∴y=-x+90.
(2)由题图可知,当乙壶中的水温是78 ℃时,x=216.
将x=216代入y=-x+90,
得-×216+90=72.
∴当乙壶中的水温是78 ℃时,甲壶中水的温度是72 ℃.
(3)同(1)求得乙壶中的水温y与x的函数关系式为y=-x+90.
由题意,得-x+90--x+90≤5,解得x≤180,
即测试180 min内(含180 min),这两个保温壶中水的温差不超过5 ℃.
例2
(1)∵S与t成正比例,
∴设S=k1t(k1≠0),
把t=1,S=4代入,得k1=4,
∴S=4t.
∵d由两部分组成,一部分与t成正比例,一部分保持不变,
∴设d=k2t+b(k2≠0),
把t=1,d=6与t=2,d=9代入,得
解得
∴d=3t+3.
点P在水平方向运动的速度vL:(8-4)÷(2-1)=4(cm/s).
点P在竖直方向的运动速度v2:(9-6)÷(2-1)=3(cm/s).
∴点P在水平方向的运动速度为4 cm/s,点P在竖直方向的运动速度为3 cm/s.
(2)根据题意,得h=12-d=12-(3t+3)=-3t+9,
∵S=4t,
∴t=S,
∴h=-3t+9=-S+9.
∵0≤t≤3,
∴0≤S≤12,
∴h=-S+9(0≤S≤12).
当h≥3时,-3t+9≥3,
解得t≤2.
答:h不少于3 cm的时长是不超过2 s.
(6年2考,9~10分)
一次函数与二次函数一共占据2道解答题,通常其中一道考查图象性质,另一道考查实际应用.近年来,一次函数的实际应用问题以图象型居多,但2024年发生改变,以文字为主阐述现实情境,通过变量关系列一次函数解决实际问题,并且与统计实现跨领域结合.这意味着2025年对一次函数实际应用的考查类型不确定性变大,综合性增强.
真题精粹·重变式——河北6年真题精选及拓展
考向1图象型一次函数应用问题 (6年1考)
1.(2023·河北23题9分)如图,这是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3km/min的速度在离地面5km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿45°仰角爬升,到4km高的A处便立刻转为水平飞行,再过1 min到达B处开始沿直线BC降落,要求1 min 后到达C(10,3)处.
(1)求OA的h关于s的函数解析式,并直接写出2号机的爬升速度.
(2)求BC的h关于s的函数解析式,并预计2号机着陆点的坐标.
(3)通过计算求出两机距离PQ不超过3km的时长.
(注:(1)及(2)中不必写s的取值范围)
考向2文字、表格型一次函数应用问题 (6年1考)
2.(2024·河北24题10分)长为300 m的春游队伍,以v(单位:m/s)的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(单位:m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(单位:s),排头与O的距离为S头(单位:m).
图1 图2
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(单位:m),求S甲与t的函数关系式(不写t的取值范围).
(2)设甲这次往返队伍的总时间为T(单位:s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
核心突破·拓思维——学科核心素养提升
题型1 图象型一次函数应用问题
小明和爸爸各买了一个保温壶,分别记为甲和乙.小明对这两个保温壶进行了保温测试,在其中同时分别倒入同样多90 ℃的热水,经过一段时间的测试发现,乙的保温性能好且这段时间内,甲、乙保温壶中的水温y(单位:℃)与时间x(单位:min)之间都近似满足一次函数关系如图所示.根据相关信息,解答下列问题:
(1)求甲壶中的水温y与x的函数关系式(不必写自变量的取值范围).
(2)当乙壶中的水温是78 ℃时,甲壶中水的温度是多少
(3)测试多长时间内,这两个保温壶中水的温差不超过5 ℃
实际问题中一次函数的确定方法
(1)第一步:甲壶中的水温y(单位:℃)与时间x(单位:min)之间近似满足一次函数关系,所以可设y=kx+b.
第二步:把图象经过的两点的坐标,代入解析式,可得方程组.
第三步:解方程组得到k与b的值,从而求得函数解析式.
以上求函数解析式所用的数学方法是待定系数法.
(2)第一步:观察图象可知,当乙壶中的水温是78 ℃时,x对应的值.
第二步:将x的值代入(1)中求得的解析式,计算得到甲壶中水的温度.
(3)第一步:同(1)求得乙壶中的水温y与x的函数关系式.
第二步:根据“两个保温壶的温差不超过5 ℃”列不等式.
第三步:解不等式,得到答案
题型2 文字、表格型实际应用问题
(2024·石家庄模拟)某电子屏上下边缘距离为12 cm,A点为左边缘上一点,一光点P从左边缘A点出发在电子屏上沿图中虚线L(直线方向)运动,到达下边缘停止,运动时间为t(单位:s),图是光点P运动过程中的某位置,P与电子屏左边缘的水平方向的距离为S cm,S与t成正比例,P与电子屏上边缘竖直距离为d cm,d由两部分组成,一部分与t成正比例,一部分保持不变,且S,d与t满足表格中的数据.
t/s 1 2
S/cm 4 8
d/cm 6 9
(1)用含t的代数式表示S与d,并直接写出P点在水平方向的运动速度vL,及在竖直方向的运动速度v2.
(2)P与电子屏下边缘竖直距离为h cm,求出h与S之间的关系式,并通过计算说明h不少于3 cm的时长是多少.
解一次函数实际应用问题的一般方法
河北省考查一次函数的实际应用问题,通常会涉及23个函数关系式,通过它们之间的联系与差异作为命题点,与方程、不等式相结合.有时会借助表格、图画、图形、光点运动等表达方式,丰富情境素材.
参考答案
真题精粹·重变式
1.(1)∵2号机爬升角度为45°,
∴OA上的点的横纵坐标相同,
∴A(4,4).
设OA的解析式为h=ks,
∴4k=4,
∴k=1,
∴OA的解析式为h=s.
∵2号机一直保持在1号机的正下方,
∴它们飞行的时间和飞行的水平距离相同.
∵2号机爬升到A处时水平方向上移动了4km,飞行的距离为4km,
又∵1号机的飞行速度为3km/min,
∴2号机的爬升速度为4÷=3 km/min.
(2)设BC的解析式为h=ms+n.
由题意得B(7,4),C(10,3),
∴解得
∴BC的解析式为h=-s+.
令h=0,则s=19.
∴预计2号机着陆点的坐标为(19,0).
(3)当PQ=3km时,h=5-3=2(km).
由h=s,得s=2;
由-s+=2,得s=13.
∴两机距离PQ不超过3km的时长为(13-2)÷3=(min).
2.(1)①排尾从位置O开始行进的时间为t (s),则排头也离开原排头t (s),
∴S头=2t+300.
②甲从排尾赶到排头的时间为300÷(2v-v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m.
甲返回时间为(t-150)s,
∴S甲=600-S甲回=600-4(t-150)=1 200-4t;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S头的值为600 m,在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=1 200-4t.
(2)T=t追及+t返回=+=,
在甲这次往返队伍的过程中队伍行进的路程为v×=400 m.
因此T与v的函数关系式为T=,此时队伍在此过程中行进的路程为400 m.
核心突破·拓思维
例1
(1)设甲壶中的水温y与x的函数关系式为y=kx+b.
∵乙壶的保温性能好,
∴甲壶的水温y与时间x的关系图象经过点(0,90),(360,60).
分别代入,得解得
∴y=-x+90.
(2)由题图可知,当乙壶中的水温是78 ℃时,x=216.
将x=216代入y=-x+90,
得-×216+90=72.
∴当乙壶中的水温是78 ℃时,甲壶中水的温度是72 ℃.
(3)同(1)求得乙壶中的水温y与x的函数关系式为y=-x+90.
由题意,得-x+90--x+90≤5,解得x≤180,
即测试180 min内(含180 min),这两个保温壶中水的温差不超过5 ℃.
例2
(1)∵S与t成正比例,
∴设S=k1t(k1≠0),
把t=1,S=4代入,得k1=4,
∴S=4t.
∵d由两部分组成,一部分与t成正比例,一部分保持不变,
∴设d=k2t+b(k2≠0),
把t=1,d=6与t=2,d=9代入,得
解得
∴d=3t+3.
点P在水平方向运动的速度vL:(8-4)÷(2-1)=4(cm/s).
点P在竖直方向的运动速度v2:(9-6)÷(2-1)=3(cm/s).
∴点P在水平方向的运动速度为4 cm/s,点P在竖直方向的运动速度为3 cm/s.
(2)根据题意,得h=12-d=12-(3t+3)=-3t+9,
∵S=4t,
∴t=S,
∴h=-3t+9=-S+9.
∵0≤t≤3,
∴0≤S≤12,
∴h=-S+9(0≤S≤12).
当h≥3时,-3t+9≥3,
解得t≤2.
答:h不少于3 cm的时长是不超过2 s.
同课章节目录
