【中考考点探究】第4节 反比例函数 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第4节 反比例函数 2025年中考一轮数学专题复习学案(河北)(含答案) | 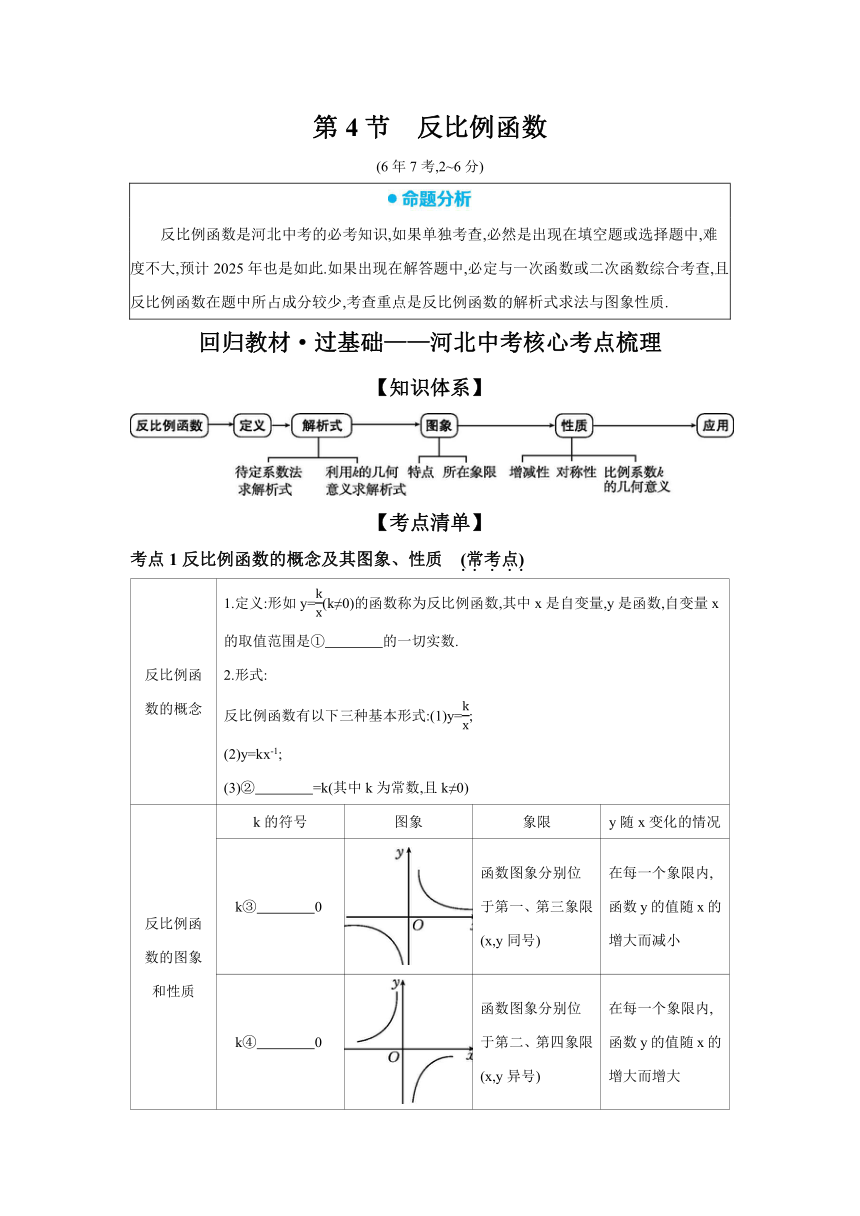 | |
| 格式 | docx | ||
| 文件大小 | 254.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:46:45 | ||
图片预览



文档简介
第4节 反比例函数
(6年7考,2~6分)
反比例函数是河北中考的必考知识,如果单独考查,必然是出现在填空题或选择题中,难度不大,预计2025年也是如此.如果出现在解答题中,必定与一次函数或二次函数综合考查,且反比例函数在题中所占成分较少,考查重点是反比例函数的解析式求法与图象性质.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1反比例函数的概念及其图象、性质 (常考点)
反比例函 数的概念 1.定义:形如y=(k≠0)的函数称为反比例函数,其中x是自变量,y是函数,自变量x的取值范围是① 的一切实数. 2.形式: 反比例函数有以下三种基本形式:(1)y=; (2)y=kx-1; (3)② =k(其中k为常数,且k≠0)
反比例函 数的图象 和性质 k的符号 图象 象限 y随x变化的情况
k③ 0 函数图象分别位于第一、第三象限(x,y同号) 在每一个象限内,函数y的值随x的增大而减小
k④ 0 函数图象分别位于第二、第四象限(x,y异号) 在每一个象限内,函数y的值随x的增大而增大
反比例函 数的图象 特征 1.由两条曲线组成,叫作双曲线. 2.图象的两个分支都无限接近x轴和y轴,但都不会与x轴和y轴相交. 3.图象是中心对称图形,⑤ 为对称中心;也是轴对称图形,两条对称轴分别是平面直角坐标系第一、第三象限和第二、第四象限的角平分线
待定系数法 只需要知道双曲线上任意一点坐标,设函数解析式,代入求出反比例函数系数k即可
考点2反比例系数的几何意义及与一次函数综合
系数k的几何意义1.意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为⑥ . 2.常见的面积类型:
反比例函数与一次函数的综合1.确定交点坐标: 【方法一】已知一个交点坐标为(a,b),则根据中心对称性,可得另一个交点坐标为⑦ . 【方法二】联立两个函数解析式,利用方程思想求解. 2.确定函数解析式:利用待定系数法,先确定交点坐标,再分别代入两个函数解析式中求解. 3.在同一坐标系中判断函数图象:充分利用函数图象与各字母系数的关系,可采用假设法,分k>0和k<0两种情况讨论,看哪个选项符合要求即可,也可逐一选项判断、排除. 4.比较函数值的大小:主要通过观察图象,图象在上方的值大,图象在下方的值小,结合交点坐标,确定解集的范围
【基础演练】
1.(冀教九上P133习题B组第1题变式)如图,A为反比例函数y=(k≠0,x<0)图象上的一点,过点A作AB⊥y轴,垂足为B,若△OAB的面积为1,则k的值为 ( )
A.1
B.-1
C.2
D.-2
2.对于反比例函数y=-,下列说法不正确的是( )
A.点(-2,1)在它的图象上
B.它的图象在第二、第四象限
C.图象关于原点对称
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1真题精粹·重变式——河北6年真题精选及拓展
考向1反比例函数图象的判断 (6年1考)
1.(2024·河北12题2分)如图,函数y=的图象所在坐标系的原点是 ( )
A.点M
B.点N
C.点P
D.点Q
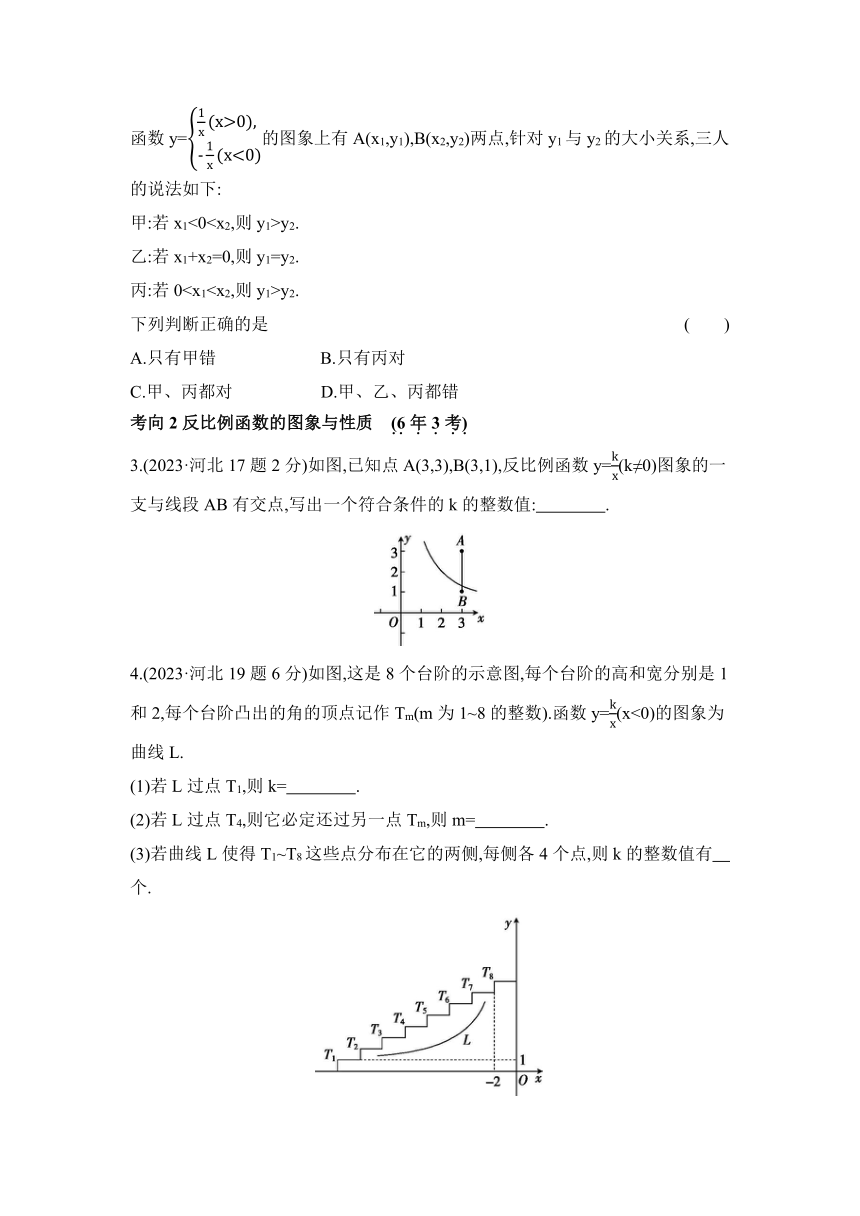
2.变设问——判断函数的增减性 函数y=的图象上有A(x1,y1),B(x2,y2)两点,针对y1与y2的大小关系,三人的说法如下: 甲:若x1<0y2. 乙:若x1+x2=0,则y1=y2. 丙:若0y2. 下列判断正确的是 ( ) A.只有甲错 B.只有丙对 C.甲、丙都对 D.甲、乙、丙都错
考向2反比例函数的图象与性质 (6年3考)
3.(2023·河北17题2分)如图,已知点A(3,3),B(3,1),反比例函数y=(k≠0)图象的一支与线段AB有交点,写出一个符合条件的k的整数值: .
4.(2023·河北19题6分)如图,这是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= .
(2)若L过点T4,则它必定还过另一点Tm,则m= .
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
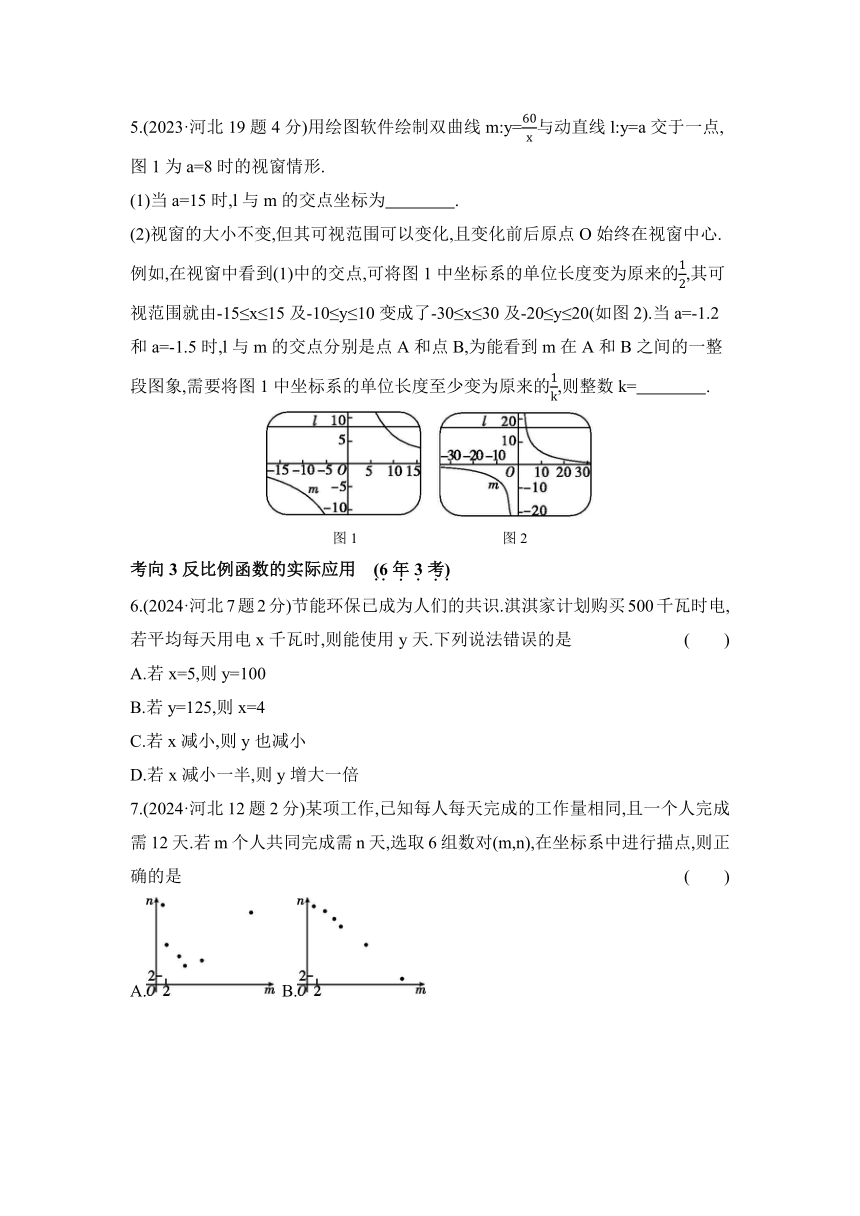
5.(2023·河北19题4分)用绘图软件绘制双曲线m:y=与动直线l:y=a交于一点,图1为a=8时的视窗情形.
(1)当a=15时,l与m的交点坐标为 .
(2)视窗的大小不变,但其可视范围可以变化,且变化前后原点O始终在视窗中心.
例如,在视窗中看到(1)中的交点,可将图1中坐标系的单位长度变为原来的,其可视范围就由-15≤x≤15及-10≤y≤10变成了-30≤x≤30及-20≤y≤20(如图2).当a=-1.2和a=-1.5时,l与m的交点分别是点A和点B,为能看到m在A和B之间的一整段图象,需要将图1中坐标系的单位长度至少变为原来的,则整数k= .
图1 图2
考向3反比例函数的实际应用 (6年3考)
6.(2024·河北7题2分)节能环保已成为人们的共识.淇淇家计划购买500千瓦时电,若平均每天用电x千瓦时,则能使用y天.下列说法错误的是 ( )
A.若x=5,则y=100
B.若y=125,则x=4
C.若x减小,则y也减小
D.若x减小一半,则y增大一倍
7.(2024·河北12题2分)某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是 ( )
A. B.
C. D.
8.(原创)如图,这是轮滑场地的截面示意图,平台AB距x轴(水平地面)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米. (1)求滑道曲线的解析式. (2)当运动员在滑道上滑至与y轴相距6米时,到地面的竖直高度为多少米
核心突破·拓思维——学科核心素养提升
题型1 双曲线的性质
(2024·河北模拟)如图,BA的延长线垂直于x轴,点A(2,1)在反比例函数y=(x>0)的图象上,点B在反比例函数y=(x>0)和y=(x>0)的图象之间,写出一个符合条件的点B的坐标: .
反比例函数虽是在河北省中考的必考知识,但比重较少,主要涉及反比例函数解析式的确定和图象的性质.经常添加平行于坐标轴的直线或线段、简单几何图形(比如一边与坐标轴平行的三角形或平行四边形)等.一般不会出现求双曲线与一次函数图象交点问题,因为列出的分式方程(组),转化为一元二次方程求解属于“超标”内容.
(2024·张家口一模)如图,在 OABC中,点C(3,0),点A(1,3),反比例函数y1=(x>0)的图象经过点B,反比例函数y2=(x>0)的图象与BC交于点F,与折线OAB交于点E.
(1)k= .
(2)若 OABC夹在y1,y2之间的整数点(横、纵坐标均为整数的点)有7个(包括边界),则m的取值范围为 .
题型2 实际问题中的反比例函数
(2024·石家庄一模)验光师通过检测发现近视眼镜的度数
y(单位:度)与镜片焦距x(单位:米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
1.(2024·沧州一模)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.图2是该台灯的电流I(单位:A)与电阻R(单位:Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是 ( )
图1 图2
(1)利用点的平移规律得到点B坐标
↓
利用待定系数法确定反比例函数关系式中k的值
↓
(2)在坐标系中画出 OABC的整数点
↓
从点B开始向左、向下找到满足题意的整数点
↓
将边界位置附近的整数点坐标代入解析式求解
反比例函数在物理、化学等其他学科中有着广泛的应用,所以经常命制跨学科综合试题.
先由点P的坐标求出反比例函数解析式,再结合图象及其增减性,判断R的不同取值范围所对应的I的取值范围.
A.当R<0.25时,I<880
B.I与R之间的函数关系式是I=(R>0)
C.当R>1 000时,I>0.22
D.当8802.(2024·河北一模)生产甲、乙两种产品需要A、B两种化工原料,具体数据如下:
A种化工原料/g B种化工原料/g
1件甲产品 300 150
1件乙产品 100 200
现生产甲产品x件,乙产品y件,恰好用完A种原料20 000 g和用去B种原料若干.
(1)求y与x之间的函数关系式.
(2)已知生产甲、乙两种产品均能售出,设每件甲产品的利润为w元(w为整数),每件乙产品的利润为20元,若B种原料不超过26 500 g,销售总利润为4 050元且x为整数,求w的值.
(1)(2)中求函数关系式,都用到了“等式变形法”.
(2)①如果一个关系式中有三个变量,需要将其中一个变量用另外两个变量中的一个表示出来,再化简变形得到解析式.
②w与x之间的函数关系式是反比例函数与常数的和.
参考答案
考点清单
①非零 ②xy ③> ④< ⑤原点
⑥|k| ⑦(-a,-b)
基础演练
1.D 2.D
真题精粹·重变式
1.A 2.A
3.k=4(答案不唯一) 4.-16 5 7
5.(1)(4,15) (2)4
提示:(1)当a=15时,y=15,
由=15,解得x=4,
∴当a=15时,l与m的交点坐标为(4,15).
(2)由=-1.2,解得x=-50,∴A(-50,-1.2);
由=-1.5,解得x=-40,∴B(-40,-1.5).
∴≤=,即k≥.
∵将题图1中坐标系的单位长度至少变为原来的,
∴整数k=4.
6.C
7.C 提示:∵一个人完成需12天,∴一人一天的工作量为.
∵m个人共同完成需n天,∴一人一天的工作量为.
∵每人每天完成的工作量相同,∴mn=12,∴n=,
∴n是m的反比例函数,
∴选取6组数对(m,n),在坐标系中描点正确的是C.
8.(1)由题意,将点A(1,18)代入y=,得18=,解得k=18,
故滑道曲线的解析式为y=.
(2)当x=6时,y==3,
故运动员到地面的竖直高度为3米.
核心突破·拓思维
例1
(2,2)(答案不唯一)
提示:∵BA的延长线垂直于x轴,
∴点B的横坐标=点A的横坐标=2,点B的纵坐标>点A的纵坐标=1.
∵点B在反比例函数y=(x>0)和y=(x>0)的图象之间,点A(2,1)在反比例函数y=(x>0)的图象上,
∴点B的纵坐标0)的值,即点B的纵坐标<,
∴符合条件的点B的横坐标为2,纵坐标大于1小于,比如(2,2)(答案不唯一).
变式训练
(1)12 (2)2提示:(1)∵OC=3,点A(1,3),
∴将点A向右平移3个单位长度得到点B(4,3),
将点B(4,3)代入y1=中,得k=12.
(2) OABC中的整数点如图所示,
将点A(1,3)代入y2=,得m=3,将点(1,2)代入y2=,得m=2,∴若 OABC夹在y1,y2之间的整数点有7个(包括边界),则m的取值范围为2例2 200
提示:设反比例函数的解析式为y=(k≠0).
∵(0.2,500)在图象上,
∴k=500×0.2=100,
∴反比例函数的解析式为y=.
当x=0.25时,y==400,
当x=0.5时,y==200,
∴度数减少了400-200=200(度).
变式训练
1.D 提示:设I与R之间的函数关系式是I=(R>0).
∵该图象经过点P(880,0.25),
∴=0.25,
∴U=220,
∴I与R之间的函数关系式是I=(R>0),故选项B不符合题意;
当R=0.25时,I=880,当R=1 000时,I=0.22.
∵反比例函数I=(R>0)中,I随R的增大而减小,
当R<0.25时,I>880,当R>1 000时,I<0.22,故选项A,C不符合题意;
∵R=880时,I=0.25,当R=1 000时,I=0.22,
∴当8802.(1)由题意得300x+100y=20 000,
∴y=-3x+200,
∴y与x之间的函数关系式为y=-3x+200.
(2)依题意得wx+20y=4 050.
∵y=200-3x,
∴w=60+.
∵150x+200y=150x+200(200-3x)≤26 500,
解得x≥30.
∵x,w为整数,
∴x=50时,w=60+=61.
(6年7考,2~6分)
反比例函数是河北中考的必考知识,如果单独考查,必然是出现在填空题或选择题中,难度不大,预计2025年也是如此.如果出现在解答题中,必定与一次函数或二次函数综合考查,且反比例函数在题中所占成分较少,考查重点是反比例函数的解析式求法与图象性质.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1反比例函数的概念及其图象、性质 (常考点)
反比例函 数的概念 1.定义:形如y=(k≠0)的函数称为反比例函数,其中x是自变量,y是函数,自变量x的取值范围是① 的一切实数. 2.形式: 反比例函数有以下三种基本形式:(1)y=; (2)y=kx-1; (3)② =k(其中k为常数,且k≠0)
反比例函 数的图象 和性质 k的符号 图象 象限 y随x变化的情况
k③ 0 函数图象分别位于第一、第三象限(x,y同号) 在每一个象限内,函数y的值随x的增大而减小
k④ 0 函数图象分别位于第二、第四象限(x,y异号) 在每一个象限内,函数y的值随x的增大而增大
反比例函 数的图象 特征 1.由两条曲线组成,叫作双曲线. 2.图象的两个分支都无限接近x轴和y轴,但都不会与x轴和y轴相交. 3.图象是中心对称图形,⑤ 为对称中心;也是轴对称图形,两条对称轴分别是平面直角坐标系第一、第三象限和第二、第四象限的角平分线
待定系数法 只需要知道双曲线上任意一点坐标,设函数解析式,代入求出反比例函数系数k即可
考点2反比例系数的几何意义及与一次函数综合
系数k的几何意义1.意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为⑥ . 2.常见的面积类型:
反比例函数与一次函数的综合1.确定交点坐标: 【方法一】已知一个交点坐标为(a,b),则根据中心对称性,可得另一个交点坐标为⑦ . 【方法二】联立两个函数解析式,利用方程思想求解. 2.确定函数解析式:利用待定系数法,先确定交点坐标,再分别代入两个函数解析式中求解. 3.在同一坐标系中判断函数图象:充分利用函数图象与各字母系数的关系,可采用假设法,分k>0和k<0两种情况讨论,看哪个选项符合要求即可,也可逐一选项判断、排除. 4.比较函数值的大小:主要通过观察图象,图象在上方的值大,图象在下方的值小,结合交点坐标,确定解集的范围
【基础演练】
1.(冀教九上P133习题B组第1题变式)如图,A为反比例函数y=(k≠0,x<0)图象上的一点,过点A作AB⊥y轴,垂足为B,若△OAB的面积为1,则k的值为 ( )
A.1
B.-1
C.2
D.-2
2.对于反比例函数y=-,下列说法不正确的是( )
A.点(-2,1)在它的图象上
B.它的图象在第二、第四象限
C.图象关于原点对称
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1
考向1反比例函数图象的判断 (6年1考)
1.(2024·河北12题2分)如图,函数y=的图象所在坐标系的原点是 ( )
A.点M
B.点N
C.点P
D.点Q
2.变设问——判断函数的增减性 函数y=的图象上有A(x1,y1),B(x2,y2)两点,针对y1与y2的大小关系,三人的说法如下: 甲:若x1<0
考向2反比例函数的图象与性质 (6年3考)
3.(2023·河北17题2分)如图,已知点A(3,3),B(3,1),反比例函数y=(k≠0)图象的一支与线段AB有交点,写出一个符合条件的k的整数值: .
4.(2023·河北19题6分)如图,这是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= .
(2)若L过点T4,则它必定还过另一点Tm,则m= .
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
5.(2023·河北19题4分)用绘图软件绘制双曲线m:y=与动直线l:y=a交于一点,图1为a=8时的视窗情形.
(1)当a=15时,l与m的交点坐标为 .
(2)视窗的大小不变,但其可视范围可以变化,且变化前后原点O始终在视窗中心.
例如,在视窗中看到(1)中的交点,可将图1中坐标系的单位长度变为原来的,其可视范围就由-15≤x≤15及-10≤y≤10变成了-30≤x≤30及-20≤y≤20(如图2).当a=-1.2和a=-1.5时,l与m的交点分别是点A和点B,为能看到m在A和B之间的一整段图象,需要将图1中坐标系的单位长度至少变为原来的,则整数k= .
图1 图2
考向3反比例函数的实际应用 (6年3考)
6.(2024·河北7题2分)节能环保已成为人们的共识.淇淇家计划购买500千瓦时电,若平均每天用电x千瓦时,则能使用y天.下列说法错误的是 ( )
A.若x=5,则y=100
B.若y=125,则x=4
C.若x减小,则y也减小
D.若x减小一半,则y增大一倍
7.(2024·河北12题2分)某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是 ( )
A. B.
C. D.
8.(原创)如图,这是轮滑场地的截面示意图,平台AB距x轴(水平地面)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米. (1)求滑道曲线的解析式. (2)当运动员在滑道上滑至与y轴相距6米时,到地面的竖直高度为多少米
核心突破·拓思维——学科核心素养提升
题型1 双曲线的性质
(2024·河北模拟)如图,BA的延长线垂直于x轴,点A(2,1)在反比例函数y=(x>0)的图象上,点B在反比例函数y=(x>0)和y=(x>0)的图象之间,写出一个符合条件的点B的坐标: .
反比例函数虽是在河北省中考的必考知识,但比重较少,主要涉及反比例函数解析式的确定和图象的性质.经常添加平行于坐标轴的直线或线段、简单几何图形(比如一边与坐标轴平行的三角形或平行四边形)等.一般不会出现求双曲线与一次函数图象交点问题,因为列出的分式方程(组),转化为一元二次方程求解属于“超标”内容.
(2024·张家口一模)如图,在 OABC中,点C(3,0),点A(1,3),反比例函数y1=(x>0)的图象经过点B,反比例函数y2=(x>0)的图象与BC交于点F,与折线OAB交于点E.
(1)k= .
(2)若 OABC夹在y1,y2之间的整数点(横、纵坐标均为整数的点)有7个(包括边界),则m的取值范围为 .
题型2 实际问题中的反比例函数
(2024·石家庄一模)验光师通过检测发现近视眼镜的度数
y(单位:度)与镜片焦距x(单位:米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
1.(2024·沧州一模)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.图2是该台灯的电流I(单位:A)与电阻R(单位:Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是 ( )
图1 图2
(1)利用点的平移规律得到点B坐标
↓
利用待定系数法确定反比例函数关系式中k的值
↓
(2)在坐标系中画出 OABC的整数点
↓
从点B开始向左、向下找到满足题意的整数点
↓
将边界位置附近的整数点坐标代入解析式求解
反比例函数在物理、化学等其他学科中有着广泛的应用,所以经常命制跨学科综合试题.
先由点P的坐标求出反比例函数解析式,再结合图象及其增减性,判断R的不同取值范围所对应的I的取值范围.
A.当R<0.25时,I<880
B.I与R之间的函数关系式是I=(R>0)
C.当R>1 000时,I>0.22
D.当880
A种化工原料/g B种化工原料/g
1件甲产品 300 150
1件乙产品 100 200
现生产甲产品x件,乙产品y件,恰好用完A种原料20 000 g和用去B种原料若干.
(1)求y与x之间的函数关系式.
(2)已知生产甲、乙两种产品均能售出,设每件甲产品的利润为w元(w为整数),每件乙产品的利润为20元,若B种原料不超过26 500 g,销售总利润为4 050元且x为整数,求w的值.
(1)(2)中求函数关系式,都用到了“等式变形法”.
(2)①如果一个关系式中有三个变量,需要将其中一个变量用另外两个变量中的一个表示出来,再化简变形得到解析式.
②w与x之间的函数关系式是反比例函数与常数的和.
参考答案
考点清单
①非零 ②xy ③> ④< ⑤原点
⑥|k| ⑦(-a,-b)
基础演练
1.D 2.D
真题精粹·重变式
1.A 2.A
3.k=4(答案不唯一) 4.-16 5 7
5.(1)(4,15) (2)4
提示:(1)当a=15时,y=15,
由=15,解得x=4,
∴当a=15时,l与m的交点坐标为(4,15).
(2)由=-1.2,解得x=-50,∴A(-50,-1.2);
由=-1.5,解得x=-40,∴B(-40,-1.5).
∴≤=,即k≥.
∵将题图1中坐标系的单位长度至少变为原来的,
∴整数k=4.
6.C
7.C 提示:∵一个人完成需12天,∴一人一天的工作量为.
∵m个人共同完成需n天,∴一人一天的工作量为.
∵每人每天完成的工作量相同,∴mn=12,∴n=,
∴n是m的反比例函数,
∴选取6组数对(m,n),在坐标系中描点正确的是C.
8.(1)由题意,将点A(1,18)代入y=,得18=,解得k=18,
故滑道曲线的解析式为y=.
(2)当x=6时,y==3,
故运动员到地面的竖直高度为3米.
核心突破·拓思维
例1
(2,2)(答案不唯一)
提示:∵BA的延长线垂直于x轴,
∴点B的横坐标=点A的横坐标=2,点B的纵坐标>点A的纵坐标=1.
∵点B在反比例函数y=(x>0)和y=(x>0)的图象之间,点A(2,1)在反比例函数y=(x>0)的图象上,
∴点B的纵坐标
∴符合条件的点B的横坐标为2,纵坐标大于1小于,比如(2,2)(答案不唯一).
变式训练
(1)12 (2)2
∴将点A向右平移3个单位长度得到点B(4,3),
将点B(4,3)代入y1=中,得k=12.
(2) OABC中的整数点如图所示,
将点A(1,3)代入y2=,得m=3,将点(1,2)代入y2=,得m=2,∴若 OABC夹在y1,y2之间的整数点有7个(包括边界),则m的取值范围为2
提示:设反比例函数的解析式为y=(k≠0).
∵(0.2,500)在图象上,
∴k=500×0.2=100,
∴反比例函数的解析式为y=.
当x=0.25时,y==400,
当x=0.5时,y==200,
∴度数减少了400-200=200(度).
变式训练
1.D 提示:设I与R之间的函数关系式是I=(R>0).
∵该图象经过点P(880,0.25),
∴=0.25,
∴U=220,
∴I与R之间的函数关系式是I=(R>0),故选项B不符合题意;
当R=0.25时,I=880,当R=1 000时,I=0.22.
∵反比例函数I=(R>0)中,I随R的增大而减小,
当R<0.25时,I>880,当R>1 000时,I<0.22,故选项A,C不符合题意;
∵R=880时,I=0.25,当R=1 000时,I=0.22,
∴当880
∴y=-3x+200,
∴y与x之间的函数关系式为y=-3x+200.
(2)依题意得wx+20y=4 050.
∵y=200-3x,
∴w=60+.
∵150x+200y=150x+200(200-3x)≤26 500,
解得x≥30.
∵x,w为整数,
∴x=50时,w=60+=61.
同课章节目录
