【中考考点探究】第4节 锐角三角函数及其应用 2025年中考一轮数学专题复习学案(河北)(含答案)
文档属性
| 名称 | 【中考考点探究】第4节 锐角三角函数及其应用 2025年中考一轮数学专题复习学案(河北)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 279.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 12:47:04 | ||
图片预览

文档简介
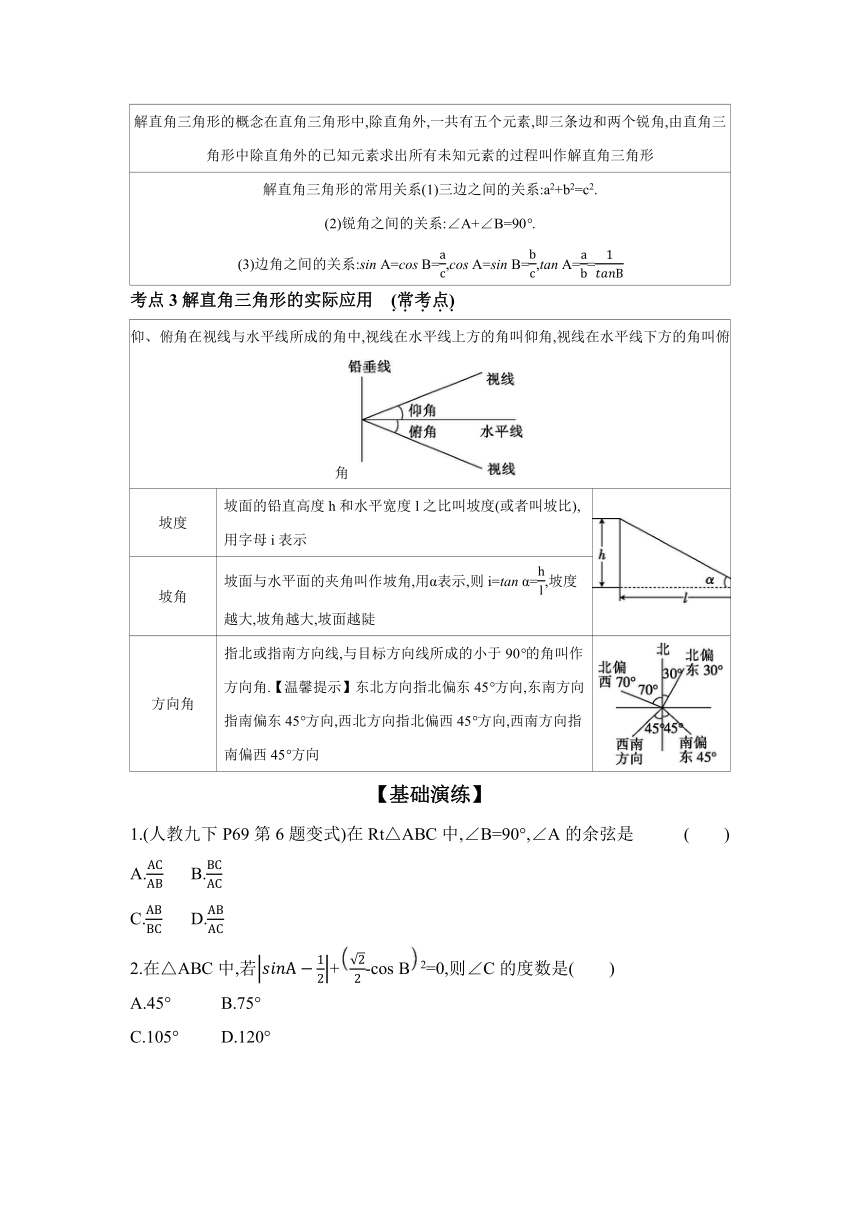
第4节 锐角三角函数及其应用
(每年1~3题,2~12分)
解直角三角形主要考查直角三角形中边角的关系和利用勾股定理(逆定理)解直角三角形,从难易度上分为两类,第一类考查直角三角形中的常见角等概念,第二类考查数学转化思想,将实际问题转化为解直角三角形的问题,预测2025年河北中考仍将延续这一特点.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1锐角三角函数的定义 (轮考点)
锐角三角函数 正弦:sin A==①
余弦:cos A==②
正切:tan A==③
特殊角的三角函数值 函数 α
30° 45° 60°
sin α ④
cos α ⑤
tan α 1
考点2解直角三角形
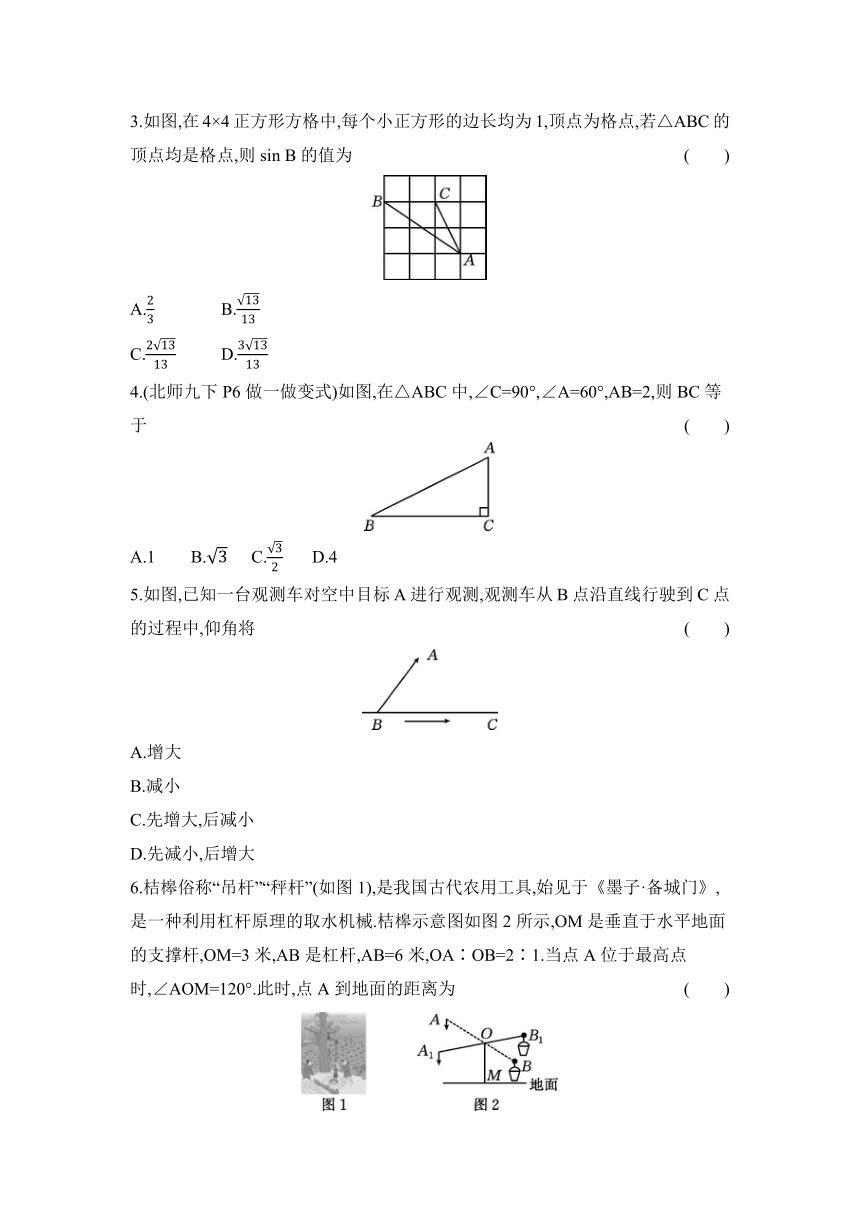
解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫作解直角三角形
解直角三角形的常用关系(1)三边之间的关系:a2+b2=c2. (2)锐角之间的关系:∠A+∠B=90°. (3)边角之间的关系:sin A=cos B=,cos A=sin B=,tan A==
考点3解直角三角形的实际应用 (常考点)
仰、俯角在视线与水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角
坡度 坡面的铅直高度h和水平宽度l之比叫坡度(或者叫坡比),用字母i表示
坡角 坡面与水平面的夹角叫作坡角,用α表示,则i=tan α=,坡度越大,坡角越大,坡面越陡
方向角 指北或指南方向线,与目标方向线所成的小于90°的角叫作方向角.【温馨提示】东北方向指北偏东45°方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向
【基础演练】
1.(人教九下P69第6题变式)在Rt△ABC中,∠B=90°,∠A的余弦是 ( )
A. B.
C. D.
2.在△ABC中,若+-cos B2=0,则∠C的度数是( )
A.45° B.75°
C.105° D.120°
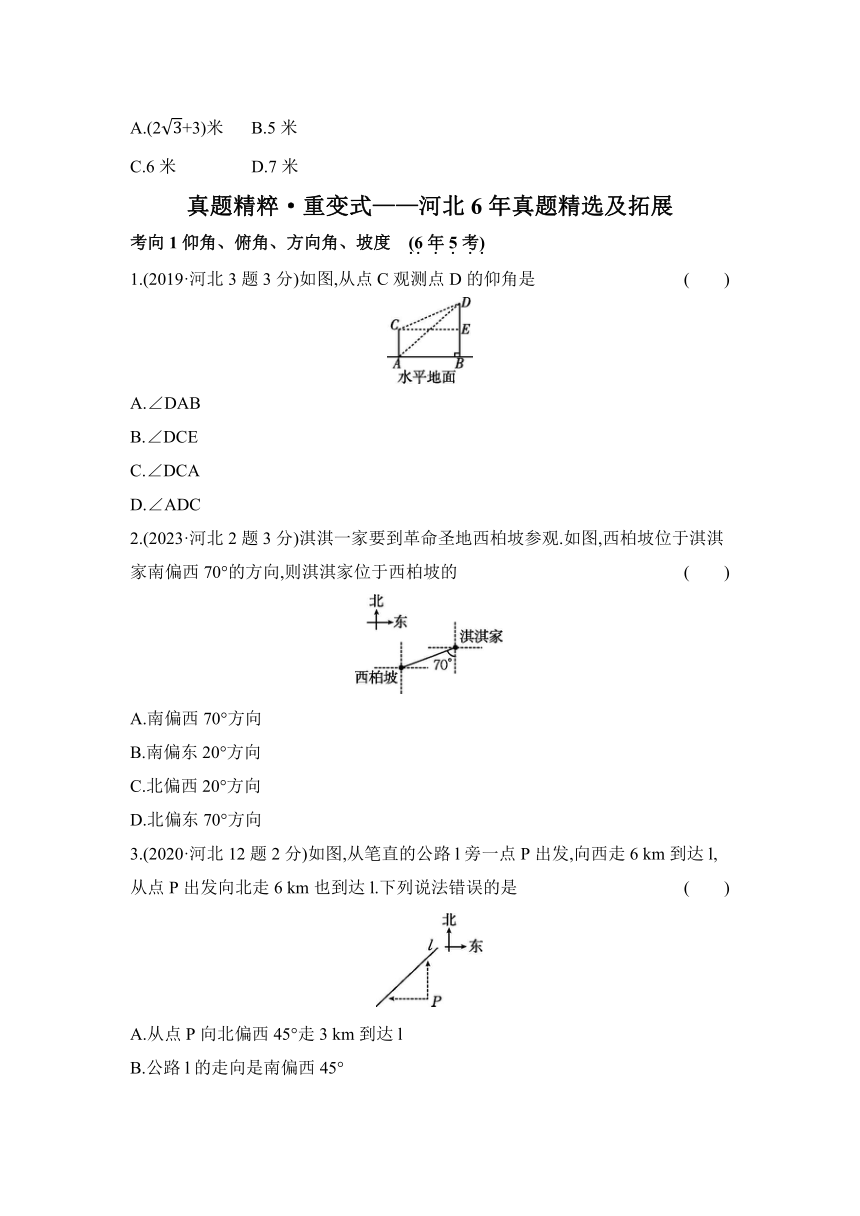
3.如图,在4×4正方形方格中,每个小正方形的边长均为1,顶点为格点,若△ABC的顶点均是格点,则sin B的值为 ( )
A. B.
C. D.
4.(北师九下P6做一做变式)如图,在△ABC中,∠C=90°,∠A=60°,AB=2,则BC等于 ( )
A.1 B. C. D.4
5.如图,已知一台观测车对空中目标A进行观测,观测车从B点沿直线行驶到C点的过程中,仰角将 ( )
A.增大
B.减小
C.先增大,后减小
D.先减小,后增大
6.桔槔俗称“吊杆”“秤杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为 ( )
A.(2+3)米 B.5米
C.6米 D.7米
真题精粹·重变式——河北6年真题精选及拓展
考向1仰角、俯角、方向角、坡度 (6年5考)
1.(2019·河北3题3分)如图,从点C观测点D的仰角是 ( )
A.∠DAB
B.∠DCE
C.∠DCA
D.∠ADC
2.(2023·河北2题3分)淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西70°的方向,则淇淇家位于西柏坡的 ( )
A.南偏西70°方向
B.南偏东20°方向
C.北偏西20°方向
D.北偏东70°方向
3.(2020·河北12题2分)如图,从笔直的公路l旁一点P出发,向西走6 km到达l,从点P出发向北走6 km也到达l.下列说法错误的是 ( )
A.从点P向北偏西45°走3 km到达l
B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3 km后,再向西走3 km到达l
考向2解直角三角形的应用 (6年2考)
4.(2024·河北22题9分)中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点P恰好看到一颗星星,此时淇淇距窗户的水平距离BQ=4 m,仰角为∠α;淇淇向前走了3 m后到达点D,透过点P恰好看到月亮,仰角为∠β,如图,已知淇淇的眼睛与水平地面BQ的距离AB=CD=1.6 m,点P到BQ的距离PQ=2.6 m,AC的延长线交PQ于点E.(注:图中所有点均在同一平面)
(1)求∠β的大小及tan α的值.
(2)求CP的长及sin∠APC的值.
5.(2022·河北24题10分)如图,某水渠的横断面是以AB为直径的半圆O,其中水面截线MN∥AB.嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,点M的俯角为7°.已知爸爸的身高为1.7 m.
(1)求∠C的大小及AB的长.
(2)请在图中画出线段DH,用其长度表示最大水深(不说理由),并求出最大水深的深度(结果保留小数点后一位).
(参考数据:tan 76°取4,取4.1)
核心突破·拓思维——学科核心素养提升
题型 锐角三角函数的应用
(2024·邢台一模)某水渠的横断面是以AC为直径的半圆O,图1表示水渠正好盛满了水,点D是水面上只能上下移动的浮漂,AB是垂直于水面线的发光物体且从点B发出光线,测得∠BDA,∠BCA分别为60°,30°,已知AD=1 m.
(1)求AC的长.
(2)如图2,把水渠中的水放掉一部分,得到水面线为MN,若的长为π m,求DN的长.tan 27°≈
近年来,锐角三角函数的“独立性”有所削弱,“工具性”有所增强.很少出现单独考查的情况,而更多的是与其他几何知识综合在一起,把三角函数作为求线段长度或角的度数的工具.
(1)先在Rt△BDA中,利用∠BDA的正切求出AB的长
↓
在Rt△BCA中,利用∠BCA的正切求出AC的长
↓
(2)根据的长和弧长公式,求得所对的圆心角度数
↓
构造垂径定理基本图形,利用锐角三角函数和勾股定理,求弦MN的一半
↓
结合点D的位置求DN的长
解直角三角形口诀
实际转化为模型,没有直角作出高;给出直角三角形的边,三角函数直接套;
不是直角三角形的边,去把方程来寻找;找出等腰三角形,解题快速又高效.
步骤 口诀 做法
1 实际转化 为模型 把实际问题转化为数学模型,画出图形,并将已知条件转化为图中的边、角或它们之间的关系
2 没有直角 作出高 若没有现成的直角三角形,可通过作高线产生直角三角形.作高线的原则是:不破坏特殊角(30°,60°,45°,120°,150°,135°)
3 利用勾股定理, 三角函数求解 若条件中给出的是直角三角形的边,利用三角函数直接求解;若给出的不是直角三角形的边,一般列方程求解;若题中有30°,60°角,利用里面的等腰三角形求解会更便捷
乒乓球台(如图1)的支架可近似看成圆弧,其示意图如图2,AC与BD所在的直线过弧EF所在圆的圆心,直线AB与弧EF所在的圆相切于点G,连接CG,DG,且AB∥EF,AG=BG.
(1)求证:∠AGC=∠BGD.
(2)若弓形EGF的高为80 cm,AG=74 cm,且tan∠BAC=,求EF的长.
锐角三角函数经常和勾股定理或相似三角形结合使用,成为解直角三角形乃至解决几何计算问题的重要工具.
参考答案
考点清单
① ② ③ ④ ⑤
基础演练
1.D 2.C 3.C 4.B 5.C 6.B
真题精粹·重变式
1.B 2.D 3.A
4.(1)由题意可得PQ⊥AE,PQ=2.6 m,AB=CD=EQ=1.6 m,AE=BQ=4 m,AC=BD=3 m,
∴CE=4-3=1(m),PE=2.6-1.6=1(m),∠CEP=90°,
∴CE=PE,
∴∠β=∠PCE=45°,tan α=tan∠PAE==.
(2)∵CE=PE=1 m,∠CEP=90°,
∴CP== m.
如图,过点C作CH⊥AP于点H.
∵tan α=tan∠PAE==,设CH=x m,则AH=4x m,
∴x2+(4x)2=AC2=9.
∴x=,
∴CH= m,
∴sin∠APC===.
5.(1)∵嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,
∴∠CAB=14°,∠CBA=90°,∴∠C=180°-∠CAB-∠CBA=76°.
∵tan C=,BC=1.7 m,∴tan 76°=,
∴AB=1.7×tan 76°≈6.8(m).
答:∠C=76°,AB的长为6.8 m.
(2)画出线段DH,如图所示:
如图,连接OM.
∵OA=OM,∠BAM=7°,∴∠OMA=∠OAM=7°.
∵AB∥MN,∴∠AMD=∠BAM=7°,∴∠OMD=14°,∴∠MOD=76°.
在Rt△MOD中,tan∠MOD=,∴tan 76°=,
∴MD=4OD.
设OD=x m,则MD=4x m,在Rt△MOD中,OM=OA=AB=3.4 m,
∴x2+(4x)2=3.42.
∵x>0,∴x=≈0.82,∴OD=0.82 m,
∴DH=OH-OD=OA-OD=3.4-0.82=2.58≈2.6(m).
答:最大水深约为2.6 m.
核心突破·拓思维
例
(1)在Rt△BDA中,∠BAD=90°,AD=1 m,∠BDA=60°,∴AB=AD·tan 60°=1×= m,
在Rt△BCA中,∠BCA=30°,
∴AC==3(m),
∴AC的长为3 m.
(2)如图,连接OM,过点O作OE⊥MN于点E,则ME=EN.
设∠AOM=n°,
∴的长==π,
∴n=27°,
∴∠AOM=27°.
∵AC∥MN,
∴∠AOM=∠OMN=27°,
在Rt△MOE中,ME=≈2OE.
根据勾股定理,可知OM2=OE2+ME2,
∴OE= m,ME= m,
∴ME=EN= m.
过点D作DD'⊥AC于点D',则DD'∥OE.
∵AC∥MN,
∴四边形DD'OE是平行四边形,
∴DE=D'O=OA-AD'=AC-AD'=-1= m,
∴DN=DE+EN=+(m),
∴DN的长为+ m.
变式训练
(1)证明:如图,延长AC,BD交于点O,则点O是弧EF所在圆的圆心,连接OG.
∵直线AB与圆O相切于点G,
∴OG⊥AB,∴∠AGO=∠BGO=90°.
∵AG=BG,∠AGO=∠BGO=90°,GO=GO,
∴△AGO ≌△BGO(SAS),
∴AO=BO,∠AOG=∠BOG.
∵CO=DO=GO,
∴∠GCO=∠CGO=∠DGO=∠GDO.
∵∠AGO=∠BGO=90°,∠CGO=∠DGO,
∴∠AGC=∠BGD.
(2)如图,连接OE,设EF与OG交于点H.
∵OG⊥AB,AG=74 cm,tan∠BAC==,
∴GO=130 cm,
∴OE=130 cm.
∵AB∥EF,OG⊥AB,
∴OG⊥EF,EF=2EH,弓形EGF的高HG=80 cm,
∴HO=GO-HG=50 cm.
在Rt△EHO中,由勾股定理得EH==120 cm,
∴EF=2EH=240 cm.
(每年1~3题,2~12分)
解直角三角形主要考查直角三角形中边角的关系和利用勾股定理(逆定理)解直角三角形,从难易度上分为两类,第一类考查直角三角形中的常见角等概念,第二类考查数学转化思想,将实际问题转化为解直角三角形的问题,预测2025年河北中考仍将延续这一特点.
回归教材·过基础——河北中考核心考点梳理
【知识体系】
【考点清单】
考点1锐角三角函数的定义 (轮考点)
锐角三角函数 正弦:sin A==①
余弦:cos A==②
正切:tan A==③
特殊角的三角函数值 函数 α
30° 45° 60°
sin α ④
cos α ⑤
tan α 1
考点2解直角三角形
解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫作解直角三角形
解直角三角形的常用关系(1)三边之间的关系:a2+b2=c2. (2)锐角之间的关系:∠A+∠B=90°. (3)边角之间的关系:sin A=cos B=,cos A=sin B=,tan A==
考点3解直角三角形的实际应用 (常考点)
仰、俯角在视线与水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角
坡度 坡面的铅直高度h和水平宽度l之比叫坡度(或者叫坡比),用字母i表示
坡角 坡面与水平面的夹角叫作坡角,用α表示,则i=tan α=,坡度越大,坡角越大,坡面越陡
方向角 指北或指南方向线,与目标方向线所成的小于90°的角叫作方向角.【温馨提示】东北方向指北偏东45°方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向
【基础演练】
1.(人教九下P69第6题变式)在Rt△ABC中,∠B=90°,∠A的余弦是 ( )
A. B.
C. D.
2.在△ABC中,若+-cos B2=0,则∠C的度数是( )
A.45° B.75°
C.105° D.120°
3.如图,在4×4正方形方格中,每个小正方形的边长均为1,顶点为格点,若△ABC的顶点均是格点,则sin B的值为 ( )
A. B.
C. D.
4.(北师九下P6做一做变式)如图,在△ABC中,∠C=90°,∠A=60°,AB=2,则BC等于 ( )
A.1 B. C. D.4
5.如图,已知一台观测车对空中目标A进行观测,观测车从B点沿直线行驶到C点的过程中,仰角将 ( )
A.增大
B.减小
C.先增大,后减小
D.先减小,后增大
6.桔槔俗称“吊杆”“秤杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为 ( )
A.(2+3)米 B.5米
C.6米 D.7米
真题精粹·重变式——河北6年真题精选及拓展
考向1仰角、俯角、方向角、坡度 (6年5考)
1.(2019·河北3题3分)如图,从点C观测点D的仰角是 ( )
A.∠DAB
B.∠DCE
C.∠DCA
D.∠ADC
2.(2023·河北2题3分)淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西70°的方向,则淇淇家位于西柏坡的 ( )
A.南偏西70°方向
B.南偏东20°方向
C.北偏西20°方向
D.北偏东70°方向
3.(2020·河北12题2分)如图,从笔直的公路l旁一点P出发,向西走6 km到达l,从点P出发向北走6 km也到达l.下列说法错误的是 ( )
A.从点P向北偏西45°走3 km到达l
B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3 km后,再向西走3 km到达l
考向2解直角三角形的应用 (6年2考)
4.(2024·河北22题9分)中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点P恰好看到一颗星星,此时淇淇距窗户的水平距离BQ=4 m,仰角为∠α;淇淇向前走了3 m后到达点D,透过点P恰好看到月亮,仰角为∠β,如图,已知淇淇的眼睛与水平地面BQ的距离AB=CD=1.6 m,点P到BQ的距离PQ=2.6 m,AC的延长线交PQ于点E.(注:图中所有点均在同一平面)
(1)求∠β的大小及tan α的值.
(2)求CP的长及sin∠APC的值.
5.(2022·河北24题10分)如图,某水渠的横断面是以AB为直径的半圆O,其中水面截线MN∥AB.嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,点M的俯角为7°.已知爸爸的身高为1.7 m.
(1)求∠C的大小及AB的长.
(2)请在图中画出线段DH,用其长度表示最大水深(不说理由),并求出最大水深的深度(结果保留小数点后一位).
(参考数据:tan 76°取4,取4.1)
核心突破·拓思维——学科核心素养提升
题型 锐角三角函数的应用
(2024·邢台一模)某水渠的横断面是以AC为直径的半圆O,图1表示水渠正好盛满了水,点D是水面上只能上下移动的浮漂,AB是垂直于水面线的发光物体且从点B发出光线,测得∠BDA,∠BCA分别为60°,30°,已知AD=1 m.
(1)求AC的长.
(2)如图2,把水渠中的水放掉一部分,得到水面线为MN,若的长为π m,求DN的长.tan 27°≈
近年来,锐角三角函数的“独立性”有所削弱,“工具性”有所增强.很少出现单独考查的情况,而更多的是与其他几何知识综合在一起,把三角函数作为求线段长度或角的度数的工具.
(1)先在Rt△BDA中,利用∠BDA的正切求出AB的长
↓
在Rt△BCA中,利用∠BCA的正切求出AC的长
↓
(2)根据的长和弧长公式,求得所对的圆心角度数
↓
构造垂径定理基本图形,利用锐角三角函数和勾股定理,求弦MN的一半
↓
结合点D的位置求DN的长
解直角三角形口诀
实际转化为模型,没有直角作出高;给出直角三角形的边,三角函数直接套;
不是直角三角形的边,去把方程来寻找;找出等腰三角形,解题快速又高效.
步骤 口诀 做法
1 实际转化 为模型 把实际问题转化为数学模型,画出图形,并将已知条件转化为图中的边、角或它们之间的关系
2 没有直角 作出高 若没有现成的直角三角形,可通过作高线产生直角三角形.作高线的原则是:不破坏特殊角(30°,60°,45°,120°,150°,135°)
3 利用勾股定理, 三角函数求解 若条件中给出的是直角三角形的边,利用三角函数直接求解;若给出的不是直角三角形的边,一般列方程求解;若题中有30°,60°角,利用里面的等腰三角形求解会更便捷
乒乓球台(如图1)的支架可近似看成圆弧,其示意图如图2,AC与BD所在的直线过弧EF所在圆的圆心,直线AB与弧EF所在的圆相切于点G,连接CG,DG,且AB∥EF,AG=BG.
(1)求证:∠AGC=∠BGD.
(2)若弓形EGF的高为80 cm,AG=74 cm,且tan∠BAC=,求EF的长.
锐角三角函数经常和勾股定理或相似三角形结合使用,成为解直角三角形乃至解决几何计算问题的重要工具.
参考答案
考点清单
① ② ③ ④ ⑤
基础演练
1.D 2.C 3.C 4.B 5.C 6.B
真题精粹·重变式
1.B 2.D 3.A
4.(1)由题意可得PQ⊥AE,PQ=2.6 m,AB=CD=EQ=1.6 m,AE=BQ=4 m,AC=BD=3 m,
∴CE=4-3=1(m),PE=2.6-1.6=1(m),∠CEP=90°,
∴CE=PE,
∴∠β=∠PCE=45°,tan α=tan∠PAE==.
(2)∵CE=PE=1 m,∠CEP=90°,
∴CP== m.
如图,过点C作CH⊥AP于点H.
∵tan α=tan∠PAE==,设CH=x m,则AH=4x m,
∴x2+(4x)2=AC2=9.
∴x=,
∴CH= m,
∴sin∠APC===.
5.(1)∵嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,
∴∠CAB=14°,∠CBA=90°,∴∠C=180°-∠CAB-∠CBA=76°.
∵tan C=,BC=1.7 m,∴tan 76°=,
∴AB=1.7×tan 76°≈6.8(m).
答:∠C=76°,AB的长为6.8 m.
(2)画出线段DH,如图所示:
如图,连接OM.
∵OA=OM,∠BAM=7°,∴∠OMA=∠OAM=7°.
∵AB∥MN,∴∠AMD=∠BAM=7°,∴∠OMD=14°,∴∠MOD=76°.
在Rt△MOD中,tan∠MOD=,∴tan 76°=,
∴MD=4OD.
设OD=x m,则MD=4x m,在Rt△MOD中,OM=OA=AB=3.4 m,
∴x2+(4x)2=3.42.
∵x>0,∴x=≈0.82,∴OD=0.82 m,
∴DH=OH-OD=OA-OD=3.4-0.82=2.58≈2.6(m).
答:最大水深约为2.6 m.
核心突破·拓思维
例
(1)在Rt△BDA中,∠BAD=90°,AD=1 m,∠BDA=60°,∴AB=AD·tan 60°=1×= m,
在Rt△BCA中,∠BCA=30°,
∴AC==3(m),
∴AC的长为3 m.
(2)如图,连接OM,过点O作OE⊥MN于点E,则ME=EN.
设∠AOM=n°,
∴的长==π,
∴n=27°,
∴∠AOM=27°.
∵AC∥MN,
∴∠AOM=∠OMN=27°,
在Rt△MOE中,ME=≈2OE.
根据勾股定理,可知OM2=OE2+ME2,
∴OE= m,ME= m,
∴ME=EN= m.
过点D作DD'⊥AC于点D',则DD'∥OE.
∵AC∥MN,
∴四边形DD'OE是平行四边形,
∴DE=D'O=OA-AD'=AC-AD'=-1= m,
∴DN=DE+EN=+(m),
∴DN的长为+ m.
变式训练
(1)证明:如图,延长AC,BD交于点O,则点O是弧EF所在圆的圆心,连接OG.
∵直线AB与圆O相切于点G,
∴OG⊥AB,∴∠AGO=∠BGO=90°.
∵AG=BG,∠AGO=∠BGO=90°,GO=GO,
∴△AGO ≌△BGO(SAS),
∴AO=BO,∠AOG=∠BOG.
∵CO=DO=GO,
∴∠GCO=∠CGO=∠DGO=∠GDO.
∵∠AGO=∠BGO=90°,∠CGO=∠DGO,
∴∠AGC=∠BGD.
(2)如图,连接OE,设EF与OG交于点H.
∵OG⊥AB,AG=74 cm,tan∠BAC==,
∴GO=130 cm,
∴OE=130 cm.
∵AB∥EF,OG⊥AB,
∴OG⊥EF,EF=2EH,弓形EGF的高HG=80 cm,
∴HO=GO-HG=50 cm.
在Rt△EHO中,由勾股定理得EH==120 cm,
∴EF=2EH=240 cm.
同课章节目录
