27.4正多边形和圆(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
27.4正多边形和圆
一、单选题
1.下列图形为正多边形的是( )
A. B. C. D.
2.若一个正多边形的边长与半径相等,则这个正多边形的中心角是( )
A.45° B.60° C.90° D.120°
3.2024年1月23日,国内在建规模最大塔式光热项目——甘肃省阿克塞汇东新能源“光热+光伏”试点项目,一万多面定日镜(如图1)全部安装完成.该项目建成后,年发电量将达17亿千瓦时.该项目采用塔式聚光热技术,使用国内首创的五边形巨蜥式定日镜,单块定日镜(如图2)的形状可近似看作正五边形,面积约为,则该正五边形的边长大约是( )(结果保留一位小数,参考数据:,,,)
A.5.2m B.4.8m C.3.7m D.2.6m
4.如图,正五边形内接于,连接,则( )
A. B. C. D.
5.如图,正多边形内接于半径相等的圆,其中正多边形的周长最大的是图形( )
A.① B.② C.③ D.无法判定
6.如图,在正六边形中,点是边的中点,是边上任意一点,若正六边形的面积是,则的值是( )
A.
B.
C.
D.由于点的位置不确定,所以的值不确定
7.正六边形的外接圆的半径与内切圆的半径之比为( )
A.1∶ B. ∶2 C.2: D. ∶1
8.要在边长为8米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为3米的圆面,则需安装这种喷水龙头的个数最少是 ( )
A.3 B.4 C.5 D.6
9.若圆的内接正六边形的半径为R,则该正六边形的内切圆的半径为( )
A.R B. C.R D.R
10.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶ B. ∶ C.3∶2 D.1∶2
二、填空题
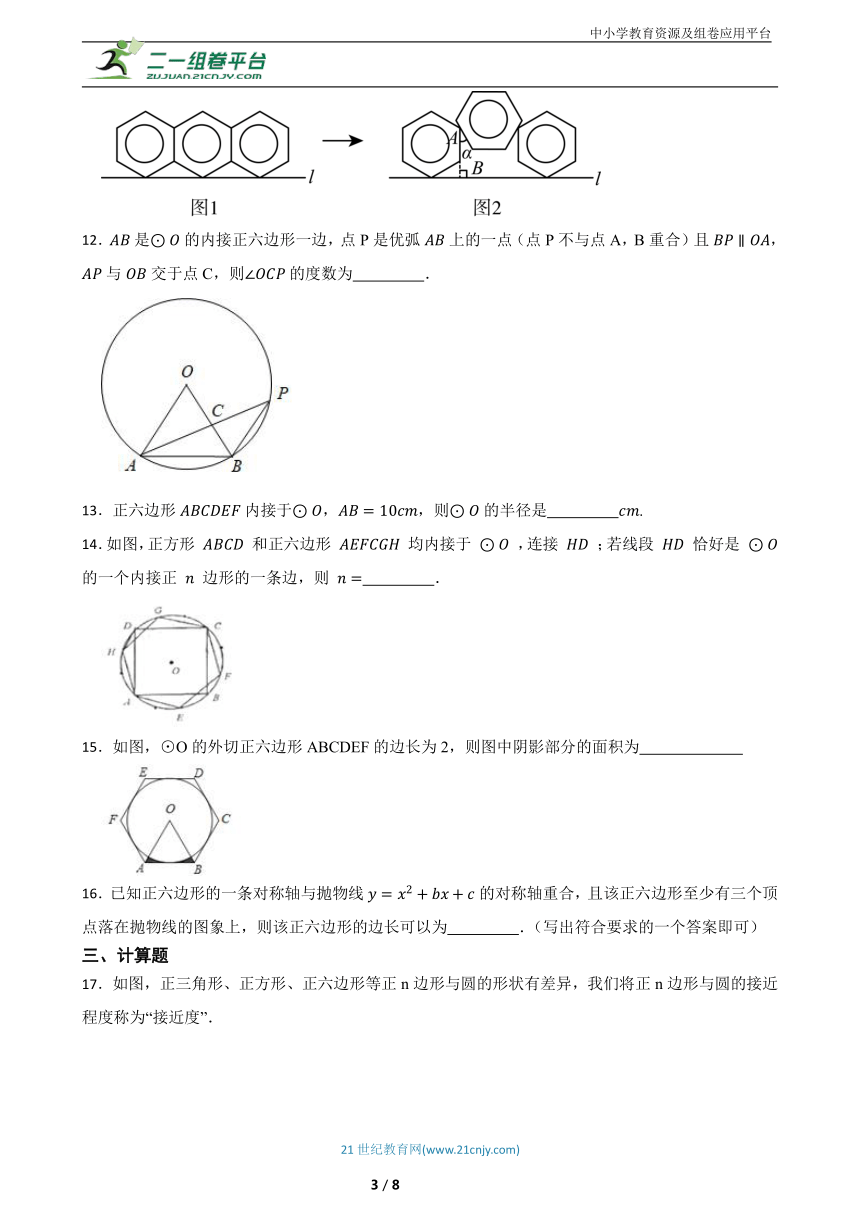
11.将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为,且各有一个顶点在直线上,两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图2所示,其中,中间正六边形的一边与直线平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线.则 .
12.是的内接正六边形一边,点P是优弧上的一点(点P不与点A,B重合)且,与交于点C,则的度数为 .
13.正六边形内接于,,则的半径是 .
14.如图,正方形 和正六边形 均内接于 ,连接 ;若线段 恰好是 的一个内接正 边形的一条边,则 .
15.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为
16.已知正六边形的一条对称轴与抛物线的对称轴重合,且该正六边形至少有三个顶点落在抛物线的图象上,则该正六边形的边长可以为 .(写出符合要求的一个答案即可)
三、计算题
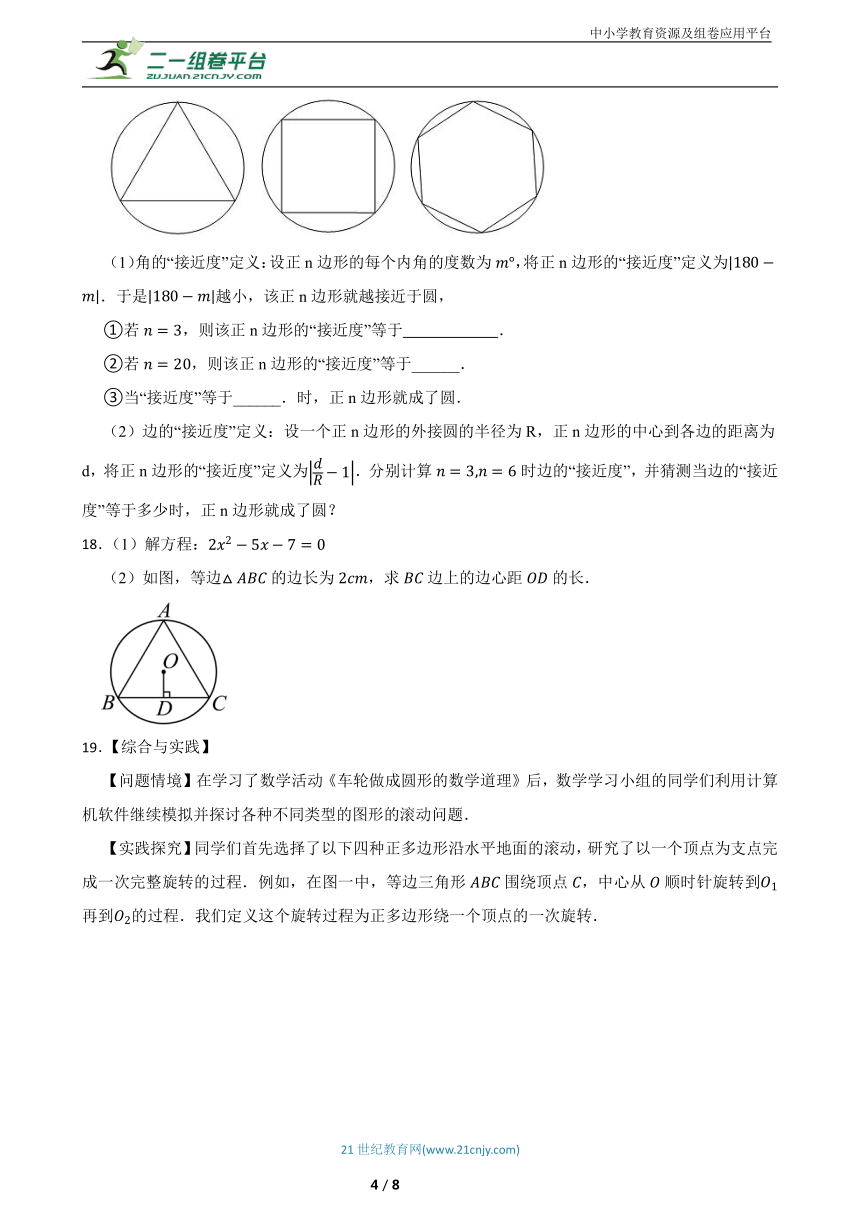
17.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)角的“接近度”定义:设正n边形的每个内角的度数为,将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
①若,则该正n边形的“接近度”等于 .
②若,则该正n边形的“接近度”等于______.
③当“接近度”等于______.时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
18.(1)解方程:
(2)如图,等边的边长为,求边上的边心距的长.
19.【综合与实践】
【问题情境】在学习了数学活动《车轮做成圆形的数学道理》后,数学学习小组的同学们利用计算机软件继续模拟并探讨各种不同类型的图形的滚动问题.
【实践探究】同学们首先选择了以下四种正多边形沿水平地面的滚动,研究了以一个顶点为支点完成一次完整旋转的过程.例如,在图一中,等边三角形围绕顶点,中心从顺时针旋转到再到的过程.我们定义这个旋转过程为正多边形绕一个顶点的一次旋转.
(1)我们学习了图二中正方形绕一个顶点的一次旋转角度为,即是正方形的中心角度数,也是外角度数.那么等边三角形绕一个顶点的一次旋转角度为______;正五边形绕一个顶点的一次旋转角度为______;正边形绕一个顶点的一次旋转角度为______;
【深入探究】同学们继续模拟并探究,如果不是沿着水平地面滚动又会是怎样的情况?
(2)如图五,半径为2的正五边形在另一个相同半径的正五边形的边上顺时针滚动,初始时正五边形绕顶点的一次旋转中,中心旋转到,则这一次旋转的旋转角度是多大?沿正五边形滚动一周后回到原来的位置,中心的运动路径长为多少?
【问题解决】如果将正多边形变化为其他图形又会是怎样的情况呢?
(3)如图六,点为上的点,,,由弦及弧组成的类似扇形的图形沿着水平地面顺时针滚动一周,直接写出圆心的运动路径的长.
四、解答题
20.如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
21.如图①,是的直径,,点C在上且位于直线上方,将半径绕点O顺时针旋转,点C的对应点为点D,连接,.
(1)以为边的内接正多边形的边数为 ;
(2)当直径平分时,求的长;
(3)如图②,连接并延长,交的延长线于点E,当是等腰三角形时,直接写出扇形的面积.
答案解析部分
1.【答案】D
【知识点】圆内接正多边形
2.【答案】B
【知识点】圆内接正多边形
3.【答案】A
【知识点】等腰三角形的判定与性质;圆内接正多边形;解直角三角形的其他实际应用
4.【答案】D
【知识点】多边形内角与外角;圆内接正多边形
5.【答案】C
【知识点】圆内接正多边形
6.【答案】A
【知识点】圆内接正多边形
7.【答案】C
【知识点】圆内接正多边形
8.【答案】B
【知识点】勾股定理;圆内接正多边形
9.【答案】D
【知识点】圆内接正多边形
10.【答案】B
【知识点】勾股定理;圆内接正多边形;锐角三角函数的定义
11.【答案】
【知识点】平行线的性质;圆内接正多边形
12.【答案】90°
【知识点】平行线的性质;圆内接正多边形
13.【答案】10
【知识点】圆内接正多边形
14.【答案】12
【知识点】圆内接正多边形
15.【答案】﹣
【知识点】圆内接正多边形
16.【答案】
【知识点】圆内接正多边形
17.【答案】(1)①120;②18;③0
(2)时,;时,,当边的“接近度”等于0时,正n边形就成了圆
【知识点】多边形内角与外角;圆内接正多边形
18.【答案】(1),;(2)
【知识点】因式分解法解一元二次方程;圆内接正多边形;解直角三角形
19.【答案】(1);(2);;(3)
【知识点】多边形内角与外角;圆内接正多边形;弧长的计算
20.【答案】解:∵正n边形边长为a,OM⊥AB,OA=OB,
∴AM= AB= a,
∵边心距为r,
∴正n边形的半径R= = = ;
∴周长P=na;
∴面积S=nS△OAB=n× a×r= nar
【知识点】圆内接正多边形
21.【答案】(1)9
(2)
(3)扇形的面积为或或
【知识点】圆周角定理;圆内接正多边形;弧长的计算;扇形面积的计算
21世纪教育网(www.21cnjy.com)
5 / 8
27.4正多边形和圆
一、单选题
1.下列图形为正多边形的是( )
A. B. C. D.
2.若一个正多边形的边长与半径相等,则这个正多边形的中心角是( )
A.45° B.60° C.90° D.120°
3.2024年1月23日,国内在建规模最大塔式光热项目——甘肃省阿克塞汇东新能源“光热+光伏”试点项目,一万多面定日镜(如图1)全部安装完成.该项目建成后,年发电量将达17亿千瓦时.该项目采用塔式聚光热技术,使用国内首创的五边形巨蜥式定日镜,单块定日镜(如图2)的形状可近似看作正五边形,面积约为,则该正五边形的边长大约是( )(结果保留一位小数,参考数据:,,,)
A.5.2m B.4.8m C.3.7m D.2.6m
4.如图,正五边形内接于,连接,则( )
A. B. C. D.
5.如图,正多边形内接于半径相等的圆,其中正多边形的周长最大的是图形( )
A.① B.② C.③ D.无法判定
6.如图,在正六边形中,点是边的中点,是边上任意一点,若正六边形的面积是,则的值是( )
A.
B.
C.
D.由于点的位置不确定,所以的值不确定
7.正六边形的外接圆的半径与内切圆的半径之比为( )
A.1∶ B. ∶2 C.2: D. ∶1
8.要在边长为8米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为3米的圆面,则需安装这种喷水龙头的个数最少是 ( )
A.3 B.4 C.5 D.6
9.若圆的内接正六边形的半径为R,则该正六边形的内切圆的半径为( )
A.R B. C.R D.R
10.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶ B. ∶ C.3∶2 D.1∶2
二、填空题
11.将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为,且各有一个顶点在直线上,两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图2所示,其中,中间正六边形的一边与直线平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线.则 .
12.是的内接正六边形一边,点P是优弧上的一点(点P不与点A,B重合)且,与交于点C,则的度数为 .
13.正六边形内接于,,则的半径是 .
14.如图,正方形 和正六边形 均内接于 ,连接 ;若线段 恰好是 的一个内接正 边形的一条边,则 .
15.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为
16.已知正六边形的一条对称轴与抛物线的对称轴重合,且该正六边形至少有三个顶点落在抛物线的图象上,则该正六边形的边长可以为 .(写出符合要求的一个答案即可)
三、计算题
17.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)角的“接近度”定义:设正n边形的每个内角的度数为,将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
①若,则该正n边形的“接近度”等于 .
②若,则该正n边形的“接近度”等于______.
③当“接近度”等于______.时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
18.(1)解方程:
(2)如图,等边的边长为,求边上的边心距的长.
19.【综合与实践】
【问题情境】在学习了数学活动《车轮做成圆形的数学道理》后,数学学习小组的同学们利用计算机软件继续模拟并探讨各种不同类型的图形的滚动问题.
【实践探究】同学们首先选择了以下四种正多边形沿水平地面的滚动,研究了以一个顶点为支点完成一次完整旋转的过程.例如,在图一中,等边三角形围绕顶点,中心从顺时针旋转到再到的过程.我们定义这个旋转过程为正多边形绕一个顶点的一次旋转.
(1)我们学习了图二中正方形绕一个顶点的一次旋转角度为,即是正方形的中心角度数,也是外角度数.那么等边三角形绕一个顶点的一次旋转角度为______;正五边形绕一个顶点的一次旋转角度为______;正边形绕一个顶点的一次旋转角度为______;
【深入探究】同学们继续模拟并探究,如果不是沿着水平地面滚动又会是怎样的情况?
(2)如图五,半径为2的正五边形在另一个相同半径的正五边形的边上顺时针滚动,初始时正五边形绕顶点的一次旋转中,中心旋转到,则这一次旋转的旋转角度是多大?沿正五边形滚动一周后回到原来的位置,中心的运动路径长为多少?
【问题解决】如果将正多边形变化为其他图形又会是怎样的情况呢?
(3)如图六,点为上的点,,,由弦及弧组成的类似扇形的图形沿着水平地面顺时针滚动一周,直接写出圆心的运动路径的长.
四、解答题
20.如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
21.如图①,是的直径,,点C在上且位于直线上方,将半径绕点O顺时针旋转,点C的对应点为点D,连接,.
(1)以为边的内接正多边形的边数为 ;
(2)当直径平分时,求的长;
(3)如图②,连接并延长,交的延长线于点E,当是等腰三角形时,直接写出扇形的面积.
答案解析部分
1.【答案】D
【知识点】圆内接正多边形
2.【答案】B
【知识点】圆内接正多边形
3.【答案】A
【知识点】等腰三角形的判定与性质;圆内接正多边形;解直角三角形的其他实际应用
4.【答案】D
【知识点】多边形内角与外角;圆内接正多边形
5.【答案】C
【知识点】圆内接正多边形
6.【答案】A
【知识点】圆内接正多边形
7.【答案】C
【知识点】圆内接正多边形
8.【答案】B
【知识点】勾股定理;圆内接正多边形
9.【答案】D
【知识点】圆内接正多边形
10.【答案】B
【知识点】勾股定理;圆内接正多边形;锐角三角函数的定义
11.【答案】
【知识点】平行线的性质;圆内接正多边形
12.【答案】90°
【知识点】平行线的性质;圆内接正多边形
13.【答案】10
【知识点】圆内接正多边形
14.【答案】12
【知识点】圆内接正多边形
15.【答案】﹣
【知识点】圆内接正多边形
16.【答案】
【知识点】圆内接正多边形
17.【答案】(1)①120;②18;③0
(2)时,;时,,当边的“接近度”等于0时,正n边形就成了圆
【知识点】多边形内角与外角;圆内接正多边形
18.【答案】(1),;(2)
【知识点】因式分解法解一元二次方程;圆内接正多边形;解直角三角形
19.【答案】(1);(2);;(3)
【知识点】多边形内角与外角;圆内接正多边形;弧长的计算
20.【答案】解:∵正n边形边长为a,OM⊥AB,OA=OB,
∴AM= AB= a,
∵边心距为r,
∴正n边形的半径R= = = ;
∴周长P=na;
∴面积S=nS△OAB=n× a×r= nar
【知识点】圆内接正多边形
21.【答案】(1)9
(2)
(3)扇形的面积为或或
【知识点】圆周角定理;圆内接正多边形;弧长的计算;扇形面积的计算
21世纪教育网(www.21cnjy.com)
5 / 8
