28.3.2容易误导读者的统计图(含答案)
文档属性
| 名称 | 28.3.2容易误导读者的统计图(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 635.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
28.3.2容易误导读者的统计图
一、单选题
1.已知一组数据的最大值为46,最小值为27,在绘制频数分布直方图时,取组距为3,则这组数据应分成( )
A.5组 B.6组 C.7组 D.8组
2.近年来我国航空事业取得重大突破,大大激发了国民对航天的热情和兴趣,某学校在全校范围内积极开展了航空航天知识竞赛,然后随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如图所示的频数分布直方图,下列说法不正确的是( )
A.样本容量为40
B.样本中得分在70.5~80.5的人数为14人
C.样本中得分在50.5~60.5的人数占总人数的12%
D.全校成绩在90分以上的占5%左右分数/分
3.一个容量为80的样本中,最大数是141,最小数是50,取组距为10,可以分成( )组
A.10组 B.9组 C.8组 D.7组
4.为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是
A.本次抽样调查的样本容量为50
B.估计该小区按第一档电价交费的居民户数最多
C.该小区按第二档电价交费的居民有240户
D.该小区按第三档电价交费的居民比例约为
5.某校为了了解学生在校吃午餐所需的时间,抽查了20名学生在校吃午餐所需的时间,获得数据(单位:):10,12,15,10,16,18,19,18,20,18,18,20,28,22,31,20,15,16,21,16.若将这些数据以为组距进行分组,则组数是( )
A.4 B.5 C.6 D.7
6.右图是某校七年级(2)班学生在一次体检中每分钟心跳次数的频数直方图(次数均为整数).该班李红同学参加了此次体检,她心跳每分钟68次,下列说法:
①李红每分钟心跳次数落在第1小组;②第3小组的频数为0.15;③每分钟心跳次数低于80次的人数占该班体检人数的.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
7.已知数据:25,24,27,25,21,23,25,29,27,28,25,24,26,28,26,27,30,22,26,25.在列频数分布表时,如果取组距为2,那么落在24.5~26.5这一组的频率是( )
A.0.3 B.0.4 C.0.5 D.0.6
8.对50个数据进行统计,频率分布表中,54.5~57.5这一组的频率为0.12.那么估计总体数据落在54.5~57.5之间的约有( )
A.12个 B.30个 C.24个 D.6个
9.学校从400名学生中抽查20名学生的视力,在得到的频率分布表中,有一组的频率是0.2,那么它的频数是( )
A.4 B.80 C.100 D.200
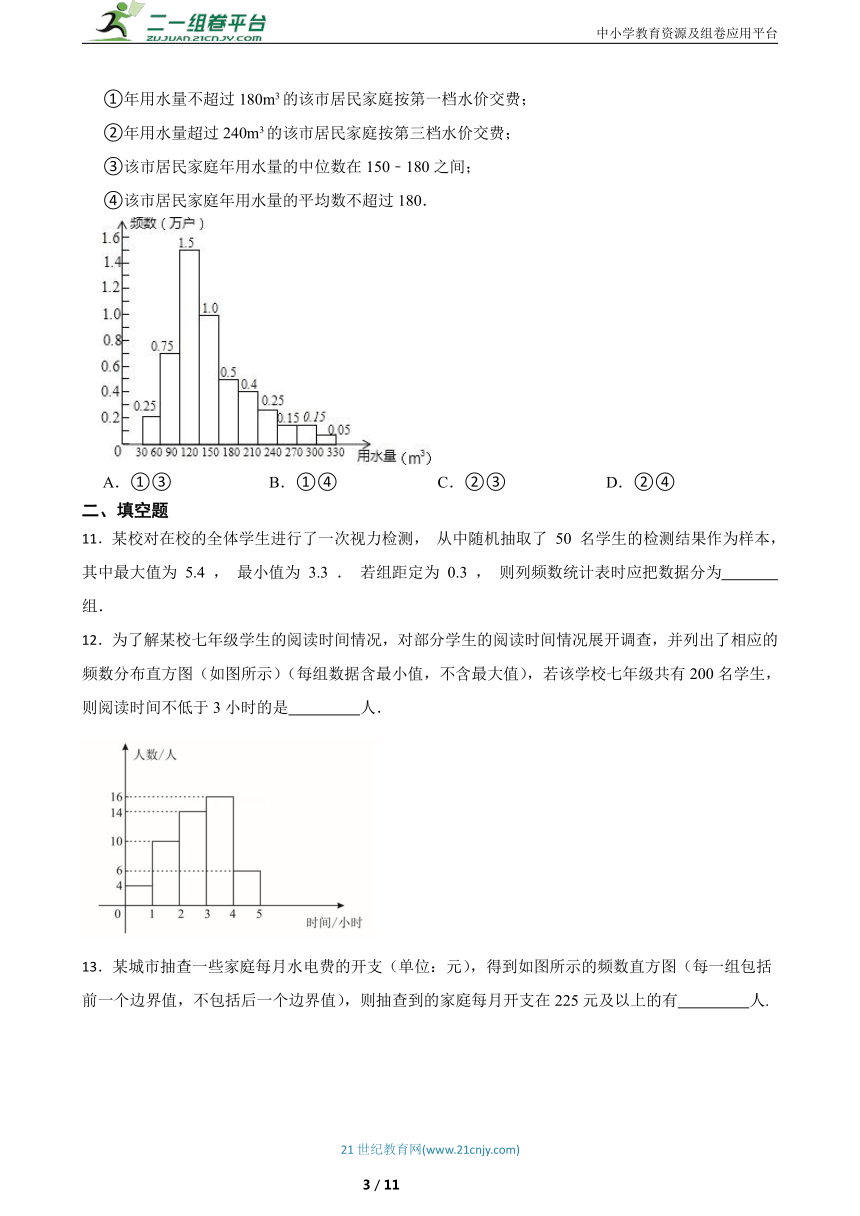
10.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
A.①③ B.①④ C.②③ D.②④
二、填空题
11.某校对在校的全体学生进行了一次视力检测, 从中随机抽取了 50 名学生的检测结果作为样本, 其中最大值为 5.4 , 最小值为 3.3 . 若组距定为 0.3 , 则列频数统计表时应把数据分为 组.
12.为了解某校七年级学生的阅读时间情况,对部分学生的阅读时间情况展开调查,并列出了相应的频数分布直方图(如图所示)(每组数据含最小值,不含最大值),若该学校七年级共有200名学生,则阅读时间不低于3小时的是 人.
13.某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有 人.
14.某校在清明节期间开展“缅怀先烈,放飞中国梦想”征文评比活动,共征集到论文160篇,对论文评比的分数(分数为整数)整理后,画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有 篇.
15.在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是 .
三、计算题
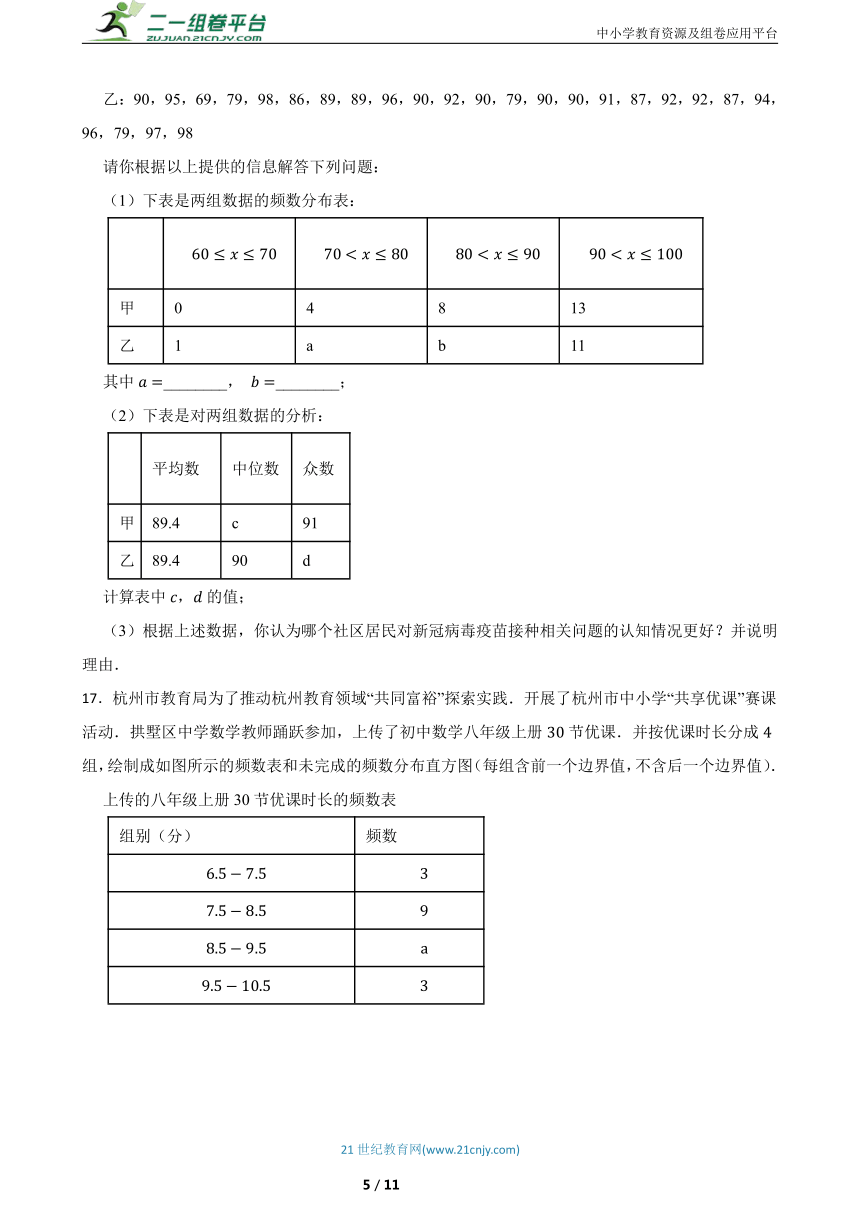
16.年国家实施新冠病毒疫苗全民接种计划,为了调查城乡居民对新冠病毒疫苗接种相关问题的认知情况(以分计),随机抽取了甲、乙两个社区各名居民的调查问卷结果,相关数据汇总如下:
甲:95,85,98,86,77,87,96,88,91,89,89,91,90,79,91,91,80,91,92,80,93,95,97,98,86
乙:90,95,69,79,98,86,89,89,96,90,92,90,79,90,90,91,87,92,92,87,94,96,79,97,98
请你根据以上提供的信息解答下列问题:
(1)下表是两组数据的频数分布表:
甲 0 4 8 13
乙 1 a b 11
其中________, ________;
(2)下表是对两组数据的分析:
平均数 中位数 众数
甲 89.4 c 91
乙 89.4 90 d
计算表中,的值;
(3)根据上述数据,你认为哪个社区居民对新冠病毒疫苗接种相关问题的认知情况更好?并说明理由.
17.杭州市教育局为了推动杭州教育领域“共同富裕”探索实践.开展了杭州市中小学“共享优课”赛课活动.拱墅区中学数学教师踊跃参加,上传了初中数学八年级上册节优课.并按优课时长分成组,绘制成如图所示的频数表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
上传的八年级上册30节优课时长的频数表
组别(分) 频数
(1)求的值,并把频数分布直方图补充完整;
(2)若要播放完这节优课(按正常速度完整播放,不考虑衔接的时间),试通过计算说明:总播放时长超过小时.
四、解答题
18.学校九年级共有50名女同学选考1min跳绳,根据测试评分标准,将她们的成绩进行统计后分为A、B、C、D四等,并绘制了下面的扇形统计图和频数分布表(注:6~7的意义为大于等于6分且小于7分,其余类似).
频数分布表
等级 分值 1min跳绳数/次 频数
A 9﹣10 150﹣170 4
8﹣9 140﹣150 12
B 7﹣8 130﹣140 17
6﹣7 120﹣130 m
C 5﹣6 110﹣120 0
4﹣5 90﹣110 n
D 3﹣4 70﹣90 1
0﹣3 0﹣70 0
(1)等级A人数的百分比是 ;
(2)求m、n的值;
(3)在抽取的这个样本中,哪个分数段的学生最多?请你帮助老师计算这次1min跳绳测试的及格率[6分以上为及格].
19.某玩具公司承接了第19庙杭州亚运会吉祥物公仔的生产任务,现对一批公仔进行抽检,其结果统计如下,请根据表中数据,回答问题:
抽取的公仔数n 10 100 1000 2000 3000
优等品的频数m 9 96 962 1920 2880
优等品的频率 0.9 0.96 a 0.96 b
(1)________;________.
(2)估计从这批公仔中任意抽取1只公仔是优等品的概率是________.(精确到0.01)
(3)若该公司这一批次生产了10000只公仔,估计这批公仔中优等品大约有多少只?
20.运动是一切生命的源泉,运动使人健康、使人聪明、使人快乐,运动不仅能改变人的体质,更能改变人的品格,某中学为了解学生一周在家运动时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将收集的数据整理分析,共分为四(,其中每周运动时间不少于小时为达标),绘制了如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)在这次抽样调查中,共调查了多少名学生;
(2)求C组人数,并请补全频数分布直方图;
(3)计算在扇形统计图中组所对应扇形的圆心角的度数;
(4)若该校有学生人,试估计该校学生一周在家运动时长不足小时的人数.
21.随着快递行业在农村的深入发展,全国各地的特色农产品有了更广阔的销售空间.不同的快递公司在配送、服务、收费和投递范围等方面各具优势,某农产品种植户经过前期调研,打算从甲、乙两家快递公司中选择一家合作.为此,该种植户收集了10家农产品种植户对两家公司的相关评价,并整理、描述、分析如下:
配送速度和服务质量得分统计表
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 m 7
乙 8 8 7
(1)补全频数分布直方图,扇形统计图中圆心角α的度数是 ;
(2)表格中的m= ; (填“”“=”或“”);
(3)如果A,B,C三家农产品种植户分别从甲、乙两个快递公司中任选一个公司合作,求三家种植户选择同一快递公司的概率.
答案解析部分
1.【答案】C
【知识点】频数(率)分布直方图
2.【答案】C
【知识点】总体、个体、样本、样本容量;用样本估计总体;频数(率)分布直方图
3.【答案】A
【知识点】频数(率)分布直方图
4.【答案】C
【知识点】频数(率)分布直方图
5.【答案】C
【知识点】频数(率)分布直方图
6.【答案】B
【知识点】频数(率)分布直方图
7.【答案】B
【知识点】频数(率)分布表
8.【答案】D
【知识点】频数(率)分布表
9.【答案】A
【知识点】频数(率)分布表
10.【答案】B
【知识点】频数(率)分布直方图;加权平均数及其计算
11.【答案】8
【知识点】频数(率)分布直方图
12.【答案】88
【知识点】频数(率)分布直方图
13.【答案】11
【知识点】频数(率)分布直方图
14.【答案】27
【知识点】频数(率)分布直方图
15.【答案】18,18,1
【知识点】频数(率)分布直方图;方差
16.【答案】(1)3,10
(2)
(3)甲社区居民对新冠病毒疫苗接种相关问题的认知情况掌握较好,理由:甲社区居民对新冠病毒疫苗接种相关问题的认知情况的中位数较高.
【知识点】频数(率)分布表;中位数;众数
17.【答案】(1)解:,补全频数分布直方图如下:
(2)解:∵(小时),
∴总播放时长超过4小时.
【知识点】频数(率)分布表;频数(率)分布直方图
18.【答案】(1)32%
(2)根据题意得:(17+m)÷50=64%,解得;m=15,.∵m+n=50﹣(4+12+17+1)=16,∴n=1;
(3)7~8 分数段的学生最多∵及格人数是:4+12+17+15=48(人),∴及格率: ×100%=96%.答:这次1分钟跳绳测试的及格人数是48人,及格率是96%.
【知识点】频数(率)分布表;扇形统计图
19.【答案】(1)0.962;0.96
(2)0.96
(3)9600只
【知识点】频数(率)分布表;利用频率估计概率
20.【答案】(1)解:组人,占比,
在这次抽样调查中,共调查了名,
故答案为:;
(2)解:组频数为:,
补全频数分布直方图如下:
(3)解:扇形统计图中组所对应扇形的圆心角的度数为:;
(4)解:该校学生一周在家运动时长不足小时的人数约为:人,
答:估计该校学生一周在家运动时长不足小时的人数约为人.
【知识点】用样本估计总体;频数(率)分布直方图;扇形统计图
21.【答案】(1)
(2),
(3)解:画树状图如下:
由树状图可知共有8种可能结果,其中三家种植户选择同一快递公司的有2种结果,
∴三家种植户选择同一快递公司的概率为.
【知识点】频数(率)分布直方图;扇形统计图;用列表法或树状图法求概率;中位数;方差
21世纪教育网(www.21cnjy.com)
2 / 11
28.3.2容易误导读者的统计图
一、单选题
1.已知一组数据的最大值为46,最小值为27,在绘制频数分布直方图时,取组距为3,则这组数据应分成( )
A.5组 B.6组 C.7组 D.8组
2.近年来我国航空事业取得重大突破,大大激发了国民对航天的热情和兴趣,某学校在全校范围内积极开展了航空航天知识竞赛,然后随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如图所示的频数分布直方图,下列说法不正确的是( )
A.样本容量为40
B.样本中得分在70.5~80.5的人数为14人
C.样本中得分在50.5~60.5的人数占总人数的12%
D.全校成绩在90分以上的占5%左右分数/分
3.一个容量为80的样本中,最大数是141,最小数是50,取组距为10,可以分成( )组
A.10组 B.9组 C.8组 D.7组
4.为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是
A.本次抽样调查的样本容量为50
B.估计该小区按第一档电价交费的居民户数最多
C.该小区按第二档电价交费的居民有240户
D.该小区按第三档电价交费的居民比例约为
5.某校为了了解学生在校吃午餐所需的时间,抽查了20名学生在校吃午餐所需的时间,获得数据(单位:):10,12,15,10,16,18,19,18,20,18,18,20,28,22,31,20,15,16,21,16.若将这些数据以为组距进行分组,则组数是( )
A.4 B.5 C.6 D.7
6.右图是某校七年级(2)班学生在一次体检中每分钟心跳次数的频数直方图(次数均为整数).该班李红同学参加了此次体检,她心跳每分钟68次,下列说法:
①李红每分钟心跳次数落在第1小组;②第3小组的频数为0.15;③每分钟心跳次数低于80次的人数占该班体检人数的.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
7.已知数据:25,24,27,25,21,23,25,29,27,28,25,24,26,28,26,27,30,22,26,25.在列频数分布表时,如果取组距为2,那么落在24.5~26.5这一组的频率是( )
A.0.3 B.0.4 C.0.5 D.0.6
8.对50个数据进行统计,频率分布表中,54.5~57.5这一组的频率为0.12.那么估计总体数据落在54.5~57.5之间的约有( )
A.12个 B.30个 C.24个 D.6个
9.学校从400名学生中抽查20名学生的视力,在得到的频率分布表中,有一组的频率是0.2,那么它的频数是( )
A.4 B.80 C.100 D.200
10.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
A.①③ B.①④ C.②③ D.②④
二、填空题
11.某校对在校的全体学生进行了一次视力检测, 从中随机抽取了 50 名学生的检测结果作为样本, 其中最大值为 5.4 , 最小值为 3.3 . 若组距定为 0.3 , 则列频数统计表时应把数据分为 组.
12.为了解某校七年级学生的阅读时间情况,对部分学生的阅读时间情况展开调查,并列出了相应的频数分布直方图(如图所示)(每组数据含最小值,不含最大值),若该学校七年级共有200名学生,则阅读时间不低于3小时的是 人.
13.某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有 人.
14.某校在清明节期间开展“缅怀先烈,放飞中国梦想”征文评比活动,共征集到论文160篇,对论文评比的分数(分数为整数)整理后,画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有 篇.
15.在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是 .
三、计算题
16.年国家实施新冠病毒疫苗全民接种计划,为了调查城乡居民对新冠病毒疫苗接种相关问题的认知情况(以分计),随机抽取了甲、乙两个社区各名居民的调查问卷结果,相关数据汇总如下:
甲:95,85,98,86,77,87,96,88,91,89,89,91,90,79,91,91,80,91,92,80,93,95,97,98,86
乙:90,95,69,79,98,86,89,89,96,90,92,90,79,90,90,91,87,92,92,87,94,96,79,97,98
请你根据以上提供的信息解答下列问题:
(1)下表是两组数据的频数分布表:
甲 0 4 8 13
乙 1 a b 11
其中________, ________;
(2)下表是对两组数据的分析:
平均数 中位数 众数
甲 89.4 c 91
乙 89.4 90 d
计算表中,的值;
(3)根据上述数据,你认为哪个社区居民对新冠病毒疫苗接种相关问题的认知情况更好?并说明理由.
17.杭州市教育局为了推动杭州教育领域“共同富裕”探索实践.开展了杭州市中小学“共享优课”赛课活动.拱墅区中学数学教师踊跃参加,上传了初中数学八年级上册节优课.并按优课时长分成组,绘制成如图所示的频数表和未完成的频数分布直方图(每组含前一个边界值,不含后一个边界值).
上传的八年级上册30节优课时长的频数表
组别(分) 频数
(1)求的值,并把频数分布直方图补充完整;
(2)若要播放完这节优课(按正常速度完整播放,不考虑衔接的时间),试通过计算说明:总播放时长超过小时.
四、解答题
18.学校九年级共有50名女同学选考1min跳绳,根据测试评分标准,将她们的成绩进行统计后分为A、B、C、D四等,并绘制了下面的扇形统计图和频数分布表(注:6~7的意义为大于等于6分且小于7分,其余类似).
频数分布表
等级 分值 1min跳绳数/次 频数
A 9﹣10 150﹣170 4
8﹣9 140﹣150 12
B 7﹣8 130﹣140 17
6﹣7 120﹣130 m
C 5﹣6 110﹣120 0
4﹣5 90﹣110 n
D 3﹣4 70﹣90 1
0﹣3 0﹣70 0
(1)等级A人数的百分比是 ;
(2)求m、n的值;
(3)在抽取的这个样本中,哪个分数段的学生最多?请你帮助老师计算这次1min跳绳测试的及格率[6分以上为及格].
19.某玩具公司承接了第19庙杭州亚运会吉祥物公仔的生产任务,现对一批公仔进行抽检,其结果统计如下,请根据表中数据,回答问题:
抽取的公仔数n 10 100 1000 2000 3000
优等品的频数m 9 96 962 1920 2880
优等品的频率 0.9 0.96 a 0.96 b
(1)________;________.
(2)估计从这批公仔中任意抽取1只公仔是优等品的概率是________.(精确到0.01)
(3)若该公司这一批次生产了10000只公仔,估计这批公仔中优等品大约有多少只?
20.运动是一切生命的源泉,运动使人健康、使人聪明、使人快乐,运动不仅能改变人的体质,更能改变人的品格,某中学为了解学生一周在家运动时长(单位:小时)的情况,从本校学生中随机抽取了部分学生进行问卷调查,并将收集的数据整理分析,共分为四(,其中每周运动时间不少于小时为达标),绘制了如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)在这次抽样调查中,共调查了多少名学生;
(2)求C组人数,并请补全频数分布直方图;
(3)计算在扇形统计图中组所对应扇形的圆心角的度数;
(4)若该校有学生人,试估计该校学生一周在家运动时长不足小时的人数.
21.随着快递行业在农村的深入发展,全国各地的特色农产品有了更广阔的销售空间.不同的快递公司在配送、服务、收费和投递范围等方面各具优势,某农产品种植户经过前期调研,打算从甲、乙两家快递公司中选择一家合作.为此,该种植户收集了10家农产品种植户对两家公司的相关评价,并整理、描述、分析如下:
配送速度和服务质量得分统计表
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 m 7
乙 8 8 7
(1)补全频数分布直方图,扇形统计图中圆心角α的度数是 ;
(2)表格中的m= ; (填“”“=”或“”);
(3)如果A,B,C三家农产品种植户分别从甲、乙两个快递公司中任选一个公司合作,求三家种植户选择同一快递公司的概率.
答案解析部分
1.【答案】C
【知识点】频数(率)分布直方图
2.【答案】C
【知识点】总体、个体、样本、样本容量;用样本估计总体;频数(率)分布直方图
3.【答案】A
【知识点】频数(率)分布直方图
4.【答案】C
【知识点】频数(率)分布直方图
5.【答案】C
【知识点】频数(率)分布直方图
6.【答案】B
【知识点】频数(率)分布直方图
7.【答案】B
【知识点】频数(率)分布表
8.【答案】D
【知识点】频数(率)分布表
9.【答案】A
【知识点】频数(率)分布表
10.【答案】B
【知识点】频数(率)分布直方图;加权平均数及其计算
11.【答案】8
【知识点】频数(率)分布直方图
12.【答案】88
【知识点】频数(率)分布直方图
13.【答案】11
【知识点】频数(率)分布直方图
14.【答案】27
【知识点】频数(率)分布直方图
15.【答案】18,18,1
【知识点】频数(率)分布直方图;方差
16.【答案】(1)3,10
(2)
(3)甲社区居民对新冠病毒疫苗接种相关问题的认知情况掌握较好,理由:甲社区居民对新冠病毒疫苗接种相关问题的认知情况的中位数较高.
【知识点】频数(率)分布表;中位数;众数
17.【答案】(1)解:,补全频数分布直方图如下:
(2)解:∵(小时),
∴总播放时长超过4小时.
【知识点】频数(率)分布表;频数(率)分布直方图
18.【答案】(1)32%
(2)根据题意得:(17+m)÷50=64%,解得;m=15,.∵m+n=50﹣(4+12+17+1)=16,∴n=1;
(3)7~8 分数段的学生最多∵及格人数是:4+12+17+15=48(人),∴及格率: ×100%=96%.答:这次1分钟跳绳测试的及格人数是48人,及格率是96%.
【知识点】频数(率)分布表;扇形统计图
19.【答案】(1)0.962;0.96
(2)0.96
(3)9600只
【知识点】频数(率)分布表;利用频率估计概率
20.【答案】(1)解:组人,占比,
在这次抽样调查中,共调查了名,
故答案为:;
(2)解:组频数为:,
补全频数分布直方图如下:
(3)解:扇形统计图中组所对应扇形的圆心角的度数为:;
(4)解:该校学生一周在家运动时长不足小时的人数约为:人,
答:估计该校学生一周在家运动时长不足小时的人数约为人.
【知识点】用样本估计总体;频数(率)分布直方图;扇形统计图
21.【答案】(1)
(2),
(3)解:画树状图如下:
由树状图可知共有8种可能结果,其中三家种植户选择同一快递公司的有2种结果,
∴三家种植户选择同一快递公司的概率为.
【知识点】频数(率)分布直方图;扇形统计图;用列表法或树状图法求概率;中位数;方差
21世纪教育网(www.21cnjy.com)
2 / 11
