第28章 样本与总体综合检测题(含答案)
文档属性
| 名称 | 第28章 样本与总体综合检测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 273.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 22:04:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第28章样本与总体综合检测题
一、单选题
1.某市期末考试中,甲校满分人数占4%,乙校满分人数占5%,比较两校满分人数( )
A.甲校多于乙校 B.甲校与乙校一样多
C.甲校少于乙校 D.不能确定
2.为了了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在25~30次的学生人数占被调查学生人数的百分比为( )
A.40% B.30% C.20% D.10%
3.下列说法不正确的是( )
A.为了解中央电视台《开学第1课》的收视率,采用抽样调查
B.为调查某单位职工学历情况占整体的百分比,采用扇形统计图
C.为调查神舟十四号飞船的零部件的质量,采用抽样调查
D.为调查某校初一班级学生的校服尺码,采用全面调查
4.以下调查中,最适合采用抽样调查的是( )
A.检测绿城南宁的空气质量
B.调查亚运会游泳决赛运动员兴奋剂的使用情况
C.公司招聘,对应聘人员进行面试
D.检查“神舟十七号”载人飞船的零件质量情况
5.以下问题中,适合采用抽样调查的是( )
A.调查某电视节目收视率情况
B.了解一沓钞票中有没有假钞
C.了解全班学生早餐喝牛奶的情况
D.检测“神舟十五号”飞船的零部件
二、填空题
6. 某次数学单元测试后, 七年级某班 50 名学生的成绩被分成 个等级. , 等级的频数分别是 ,其余的为 等级,则 等级的频率是
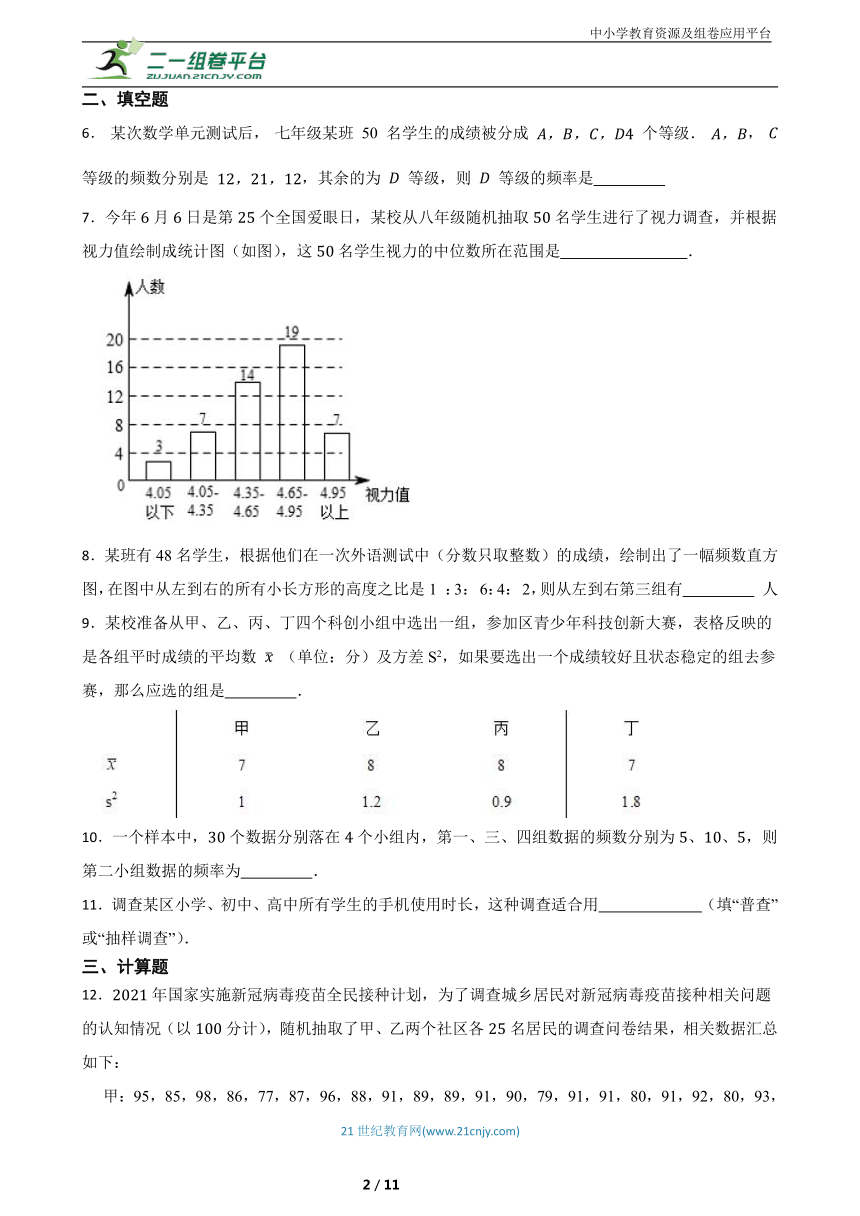
7.今年月日是第个全国爱眼日,某校从八年级随机抽取名学生进行了视力调查,并根据视力值绘制成统计图(如图),这名学生视力的中位数所在范围是 .
8.某班有48名学生,根据他们在一次外语测试中(分数只取整数)的成绩,绘制出了一幅频数直方图,在图中从左到右的所有小长方形的高度之比是1 :3: 6:4: 2,则从左到右第三组有 人
9.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数 (单位:分)及方差S2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是 .
10.一个样本中,个数据分别落在个小组内,第一、三、四组数据的频数分别为、、,则第二小组数据的频率为 .
11.调查某区小学、初中、高中所有学生的手机使用时长,这种调查适合用 (填“普查”或“抽样调查”).
三、计算题
12.年国家实施新冠病毒疫苗全民接种计划,为了调查城乡居民对新冠病毒疫苗接种相关问题的认知情况(以分计),随机抽取了甲、乙两个社区各名居民的调查问卷结果,相关数据汇总如下:
甲:95,85,98,86,77,87,96,88,91,89,89,91,90,79,91,91,80,91,92,80,93,95,97,98,86
乙:90,95,69,79,98,86,89,89,96,90,92,90,79,90,90,91,87,92,92,87,94,96,79,97,98
请你根据以上提供的信息解答下列问题:
(1)下表是两组数据的频数分布表:
甲 0 4 8 13
乙 1 a b 11
其中________, ________;
(2)下表是对两组数据的分析:
平均数 中位数 众数
甲 89.4 c 91
乙 89.4 90 d
计算表中,的值;
(3)根据上述数据,你认为哪个社区居民对新冠病毒疫苗接种相关问题的认知情况更好?并说明理由.
13.自18世纪以来一些统计学家做“抛掷质地均匀的硬币实验”获得的数据如下表
实验者 实验次数 正面朝上的频数 正面朝上的频率
布丰
德·摩根
费勒
皮尔逊
皮尔逊
罗曼诺夫斯基
(1)表中的______,______;
(2)估计硬币正面朝上的概率.(精确到)
四、解答题
14.为调查学生对客家文化的了解程度,某校从300名九年级学生中随机抽取了50名学生进行“我爱客家文化”知识问卷调查活动,对问卷调查成绩按“很好”“较好”“一般”“较差”四类统计分析,并绘制了如下扇形统计图.
(1)在抽取的学生中,成绩为“较好”的所占比例为多少?
(2)在抽取的学生中,成绩为“较差”的有多少人?
(3)根据抽查数据,估计该校九年级学生成绩为“很好”的学生有多少人?
15.中国人有在端午节这一天吃“粽子”的传统,寓意“祈福高中”.某粽子加工厂家为迎接端午的到来,组织了“浓情端午,粽叶飘香”员工包粽子比赛,规定所包粽子质量为时都符合标准,其中质量为优秀产品.现从甲乙两位员工所包粽子中各随机抽取个进行评测,质量分别如下单位::
甲:,,,,,,,,,
乙:,,,,,,,,,
分析数据如下表:
员工 平均数 中位数 众数 方差
甲 a
乙 b c
根据以上信息,解答下列问题:
(1)a= ,b= ,c= .
(2)若比赛规则的评判标准里看重所包粽子质量是否符合标准以及粽子质量的稳定性,根据抽样所得的粽子质量,你觉得哪位员工更加优秀?请说明理由.
(3)在此次比赛中,甲员工共包了个粽子,乙员工共包了个粽子,请你估计两位员工各自所包粽子质量属于“优秀产品”的个数,并判断若以此作为评判标准哪位员工更加优秀?请说明理由.
五、综合题
16.定点投篮测试规定,得6分以上为合格,得8分以上(包括8分)为优秀,甲、乙两组各随机选取15名同学的测试成绩如下:
成绩(分) 4 5 6 7 8 9
甲组(人) 1 2 5 2 1 4
乙组(人) 1 1 4 5 2 2
一分钟投篮成绩统计分析表:
统计量 平均分 中位数 众数 方差 合格率
甲组 6.8 m 6 2.56 80.0%
乙组 6.8 7 n 1.76 86.7%
(1)由上表填空m= ,n= ;
(2)你认为哪一组更优秀,请说明理由(一条理由即可);
(3)若甲组共有300人,请估计甲组中优秀的人数.
17.某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) 1 2 3 4 5 6 7 8 9
人数(名) 1 2 6 7 12 x 7 y 1
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
18.中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 中位数 众数 方差
去年 64.2 68 73 715.6
今年 56.2 a 68 629.7
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
六、实践探究题
19.[新考法——提建议,注重开放性]为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.
整理描述
初中学生视力情况统计表
视力 人数 百分比
0.6及以下 8
0.7 16
0.8 28
0.9 34
1.0
1.1及以上 46
合计 200
(1) , ;
(2)被调查的高中学生视力情况的样本容量为 ;
(3)分析处理
①小胡说:“初中学生的视力水平比高中学生的好.”请你对小胡的说法进行判断,并选择一个能反映总体的统计量说明理由;
②约定:视力未达到1.0为视力不良.若该区有26000名中学生,估计该区有多少名中学生视力不良?并对视力保护提出一条合理化建议.
答案解析部分
1.【答案】D
【知识点】频数与频率
2.【答案】A
【知识点】频数(率)分布直方图
3.【答案】C
【知识点】全面调查与抽样调查;扇形统计图
4.【答案】A
【知识点】全面调查与抽样调查
5.【答案】A
【知识点】全面调查与抽样调查
6.【答案】0.1
【知识点】频数与频率
7.【答案】4.65-4.95.
【知识点】频数(率)分布直方图;中位数
8.【答案】18
【知识点】频数(率)分布直方图
9.【答案】丙
【知识点】利用统计图表描述数据
10.【答案】
【知识点】频数与频率
11.【答案】抽样调查
【知识点】全面调查与抽样调查
12.【答案】(1)3,10
(2)
(3)甲社区居民对新冠病毒疫苗接种相关问题的认知情况掌握较好,理由:甲社区居民对新冠病毒疫苗接种相关问题的认知情况的中位数较高.
【知识点】频数(率)分布表;中位数;众数
13.【答案】(1);
(2)
【知识点】频数与频率;利用频率估计概率
14.【答案】(1)在所抽取的学生中,成绩为“较好”的占比为
(2)在所抽取的学生中,成绩为“较差”的有7人
(3)估计该校九年级学生成绩为“很好”的学生有48人
【知识点】用样本估计总体;扇形统计图
15.【答案】(1)160;161;3
(2)解:乙员工更加优秀,理由如下:
因为乙的方差小于甲的方差,
所以乙所包粽子质量质量比较稳定;
(3)解:甲员工所包粽子质量属于“优秀产品”得个数为:个,
乙员工所包粽子质量属于“优秀产品”得个数为:个,
甲员工所包粽子的优秀率为%,
乙员工所包粽子的优秀率为%,
甲员工所包粽子的优秀率大于乙员工所包粽子的优秀率,
甲员工更加优秀.
【知识点】用样本估计总体;平均数及其计算;方差;众数
16.【答案】(1)6;7
(2)解:乙组的中位数大于甲组的中位数,乙组的方差小于甲组的方差,所以乙组更优秀.
(3)解:300× =100(人).
答:甲组中优秀的人数约有100人.
【知识点】用样本估计总体;分析数据的集中趋势(平均数、中位数、众数)
17.【答案】(1)解:由表可知被调查学生中“一般”档次的有13人,所占比例是26%,所以共调查的学生数是13÷26%=50,
则调查学生中“良好”档次的人数为50×60%=30,
∴x=30﹣(12+7)=11,
y=50﹣(1+2+6+7+12+11+7+1)=3.
(2)解:
由样本数据可知“优秀”档次所占的百分比为=8%,
∴,估计九年级400名学生中为优秀档次的人数为400×8%=32
(3)解:用A、B、C表示阅读本数是8的学生,用D表示阅读9本的学生,列表得到:
A B C D
A AB AC AD
B BA BC BD
C CA CB CD
D DA DB DC
由列表可知,共12种等可能的结果,其中所抽取的2名学生中有1名阅读本数为9的有6种,所以抽取的2名学生中有1名阅读本数为9的概率为
【知识点】用样本估计总体;扇形统计图;用列表法或树状图法求概率
18.【答案】(1)64
(2)解:选择平均数,
由表可知,去年“声呐鲟”到达下游监测点的平均时间为64.2小时,而今年“声呐鲟”到达下游监测点的平均时间为56.2小时,缩短了8小时,
所以今年“声呐鲟”从长江到海洋的适应情况更好(答案不唯一,合理即可).
(3)解:1300×(尾).
答:其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有624尾中华鲟通过监测站A.
【知识点】用样本估计总体;频数(率)分布直方图;扇形统计图;分析数据的集中趋势(平均数、中位数、众数)
19.【答案】(1)68;23%
(2)320
(3)解:①小胡的说法正确,理由如下:
初中生的视力众数是1.0,高中生的视力众数是0.9,
1.0>0.9
初中学生的视力水平比高中学生的好;(理由不唯一)
②方法一:(名);
方法二:14300(名).
答:该区大约有14300名中学生视力不良.
对视力保护提出的建议是:坚持做眼保健操,加强体育锻炼,养成良好的阅读习惯,保护个人视力.(答案不唯一,合理即可)
【知识点】总体、个体、样本、样本容量;用样本估计总体;频数(率)分布表;频数(率)分布直方图;统计表;条形统计图
21世纪教育网(www.21cnjy.com)
2 / 11
第28章样本与总体综合检测题
一、单选题
1.某市期末考试中,甲校满分人数占4%,乙校满分人数占5%,比较两校满分人数( )
A.甲校多于乙校 B.甲校与乙校一样多
C.甲校少于乙校 D.不能确定
2.为了了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在25~30次的学生人数占被调查学生人数的百分比为( )
A.40% B.30% C.20% D.10%
3.下列说法不正确的是( )
A.为了解中央电视台《开学第1课》的收视率,采用抽样调查
B.为调查某单位职工学历情况占整体的百分比,采用扇形统计图
C.为调查神舟十四号飞船的零部件的质量,采用抽样调查
D.为调查某校初一班级学生的校服尺码,采用全面调查
4.以下调查中,最适合采用抽样调查的是( )
A.检测绿城南宁的空气质量
B.调查亚运会游泳决赛运动员兴奋剂的使用情况
C.公司招聘,对应聘人员进行面试
D.检查“神舟十七号”载人飞船的零件质量情况
5.以下问题中,适合采用抽样调查的是( )
A.调查某电视节目收视率情况
B.了解一沓钞票中有没有假钞
C.了解全班学生早餐喝牛奶的情况
D.检测“神舟十五号”飞船的零部件
二、填空题
6. 某次数学单元测试后, 七年级某班 50 名学生的成绩被分成 个等级. , 等级的频数分别是 ,其余的为 等级,则 等级的频率是
7.今年月日是第个全国爱眼日,某校从八年级随机抽取名学生进行了视力调查,并根据视力值绘制成统计图(如图),这名学生视力的中位数所在范围是 .
8.某班有48名学生,根据他们在一次外语测试中(分数只取整数)的成绩,绘制出了一幅频数直方图,在图中从左到右的所有小长方形的高度之比是1 :3: 6:4: 2,则从左到右第三组有 人
9.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数 (单位:分)及方差S2,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是 .
10.一个样本中,个数据分别落在个小组内,第一、三、四组数据的频数分别为、、,则第二小组数据的频率为 .
11.调查某区小学、初中、高中所有学生的手机使用时长,这种调查适合用 (填“普查”或“抽样调查”).
三、计算题
12.年国家实施新冠病毒疫苗全民接种计划,为了调查城乡居民对新冠病毒疫苗接种相关问题的认知情况(以分计),随机抽取了甲、乙两个社区各名居民的调查问卷结果,相关数据汇总如下:
甲:95,85,98,86,77,87,96,88,91,89,89,91,90,79,91,91,80,91,92,80,93,95,97,98,86
乙:90,95,69,79,98,86,89,89,96,90,92,90,79,90,90,91,87,92,92,87,94,96,79,97,98
请你根据以上提供的信息解答下列问题:
(1)下表是两组数据的频数分布表:
甲 0 4 8 13
乙 1 a b 11
其中________, ________;
(2)下表是对两组数据的分析:
平均数 中位数 众数
甲 89.4 c 91
乙 89.4 90 d
计算表中,的值;
(3)根据上述数据,你认为哪个社区居民对新冠病毒疫苗接种相关问题的认知情况更好?并说明理由.
13.自18世纪以来一些统计学家做“抛掷质地均匀的硬币实验”获得的数据如下表
实验者 实验次数 正面朝上的频数 正面朝上的频率
布丰
德·摩根
费勒
皮尔逊
皮尔逊
罗曼诺夫斯基
(1)表中的______,______;
(2)估计硬币正面朝上的概率.(精确到)
四、解答题
14.为调查学生对客家文化的了解程度,某校从300名九年级学生中随机抽取了50名学生进行“我爱客家文化”知识问卷调查活动,对问卷调查成绩按“很好”“较好”“一般”“较差”四类统计分析,并绘制了如下扇形统计图.
(1)在抽取的学生中,成绩为“较好”的所占比例为多少?
(2)在抽取的学生中,成绩为“较差”的有多少人?
(3)根据抽查数据,估计该校九年级学生成绩为“很好”的学生有多少人?
15.中国人有在端午节这一天吃“粽子”的传统,寓意“祈福高中”.某粽子加工厂家为迎接端午的到来,组织了“浓情端午,粽叶飘香”员工包粽子比赛,规定所包粽子质量为时都符合标准,其中质量为优秀产品.现从甲乙两位员工所包粽子中各随机抽取个进行评测,质量分别如下单位::
甲:,,,,,,,,,
乙:,,,,,,,,,
分析数据如下表:
员工 平均数 中位数 众数 方差
甲 a
乙 b c
根据以上信息,解答下列问题:
(1)a= ,b= ,c= .
(2)若比赛规则的评判标准里看重所包粽子质量是否符合标准以及粽子质量的稳定性,根据抽样所得的粽子质量,你觉得哪位员工更加优秀?请说明理由.
(3)在此次比赛中,甲员工共包了个粽子,乙员工共包了个粽子,请你估计两位员工各自所包粽子质量属于“优秀产品”的个数,并判断若以此作为评判标准哪位员工更加优秀?请说明理由.
五、综合题
16.定点投篮测试规定,得6分以上为合格,得8分以上(包括8分)为优秀,甲、乙两组各随机选取15名同学的测试成绩如下:
成绩(分) 4 5 6 7 8 9
甲组(人) 1 2 5 2 1 4
乙组(人) 1 1 4 5 2 2
一分钟投篮成绩统计分析表:
统计量 平均分 中位数 众数 方差 合格率
甲组 6.8 m 6 2.56 80.0%
乙组 6.8 7 n 1.76 86.7%
(1)由上表填空m= ,n= ;
(2)你认为哪一组更优秀,请说明理由(一条理由即可);
(3)若甲组共有300人,请估计甲组中优秀的人数.
17.某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) 1 2 3 4 5 6 7 8 9
人数(名) 1 2 6 7 12 x 7 y 1
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
18.中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 中位数 众数 方差
去年 64.2 68 73 715.6
今年 56.2 a 68 629.7
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.
六、实践探究题
19.[新考法——提建议,注重开放性]为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.
整理描述
初中学生视力情况统计表
视力 人数 百分比
0.6及以下 8
0.7 16
0.8 28
0.9 34
1.0
1.1及以上 46
合计 200
(1) , ;
(2)被调查的高中学生视力情况的样本容量为 ;
(3)分析处理
①小胡说:“初中学生的视力水平比高中学生的好.”请你对小胡的说法进行判断,并选择一个能反映总体的统计量说明理由;
②约定:视力未达到1.0为视力不良.若该区有26000名中学生,估计该区有多少名中学生视力不良?并对视力保护提出一条合理化建议.
答案解析部分
1.【答案】D
【知识点】频数与频率
2.【答案】A
【知识点】频数(率)分布直方图
3.【答案】C
【知识点】全面调查与抽样调查;扇形统计图
4.【答案】A
【知识点】全面调查与抽样调查
5.【答案】A
【知识点】全面调查与抽样调查
6.【答案】0.1
【知识点】频数与频率
7.【答案】4.65-4.95.
【知识点】频数(率)分布直方图;中位数
8.【答案】18
【知识点】频数(率)分布直方图
9.【答案】丙
【知识点】利用统计图表描述数据
10.【答案】
【知识点】频数与频率
11.【答案】抽样调查
【知识点】全面调查与抽样调查
12.【答案】(1)3,10
(2)
(3)甲社区居民对新冠病毒疫苗接种相关问题的认知情况掌握较好,理由:甲社区居民对新冠病毒疫苗接种相关问题的认知情况的中位数较高.
【知识点】频数(率)分布表;中位数;众数
13.【答案】(1);
(2)
【知识点】频数与频率;利用频率估计概率
14.【答案】(1)在所抽取的学生中,成绩为“较好”的占比为
(2)在所抽取的学生中,成绩为“较差”的有7人
(3)估计该校九年级学生成绩为“很好”的学生有48人
【知识点】用样本估计总体;扇形统计图
15.【答案】(1)160;161;3
(2)解:乙员工更加优秀,理由如下:
因为乙的方差小于甲的方差,
所以乙所包粽子质量质量比较稳定;
(3)解:甲员工所包粽子质量属于“优秀产品”得个数为:个,
乙员工所包粽子质量属于“优秀产品”得个数为:个,
甲员工所包粽子的优秀率为%,
乙员工所包粽子的优秀率为%,
甲员工所包粽子的优秀率大于乙员工所包粽子的优秀率,
甲员工更加优秀.
【知识点】用样本估计总体;平均数及其计算;方差;众数
16.【答案】(1)6;7
(2)解:乙组的中位数大于甲组的中位数,乙组的方差小于甲组的方差,所以乙组更优秀.
(3)解:300× =100(人).
答:甲组中优秀的人数约有100人.
【知识点】用样本估计总体;分析数据的集中趋势(平均数、中位数、众数)
17.【答案】(1)解:由表可知被调查学生中“一般”档次的有13人,所占比例是26%,所以共调查的学生数是13÷26%=50,
则调查学生中“良好”档次的人数为50×60%=30,
∴x=30﹣(12+7)=11,
y=50﹣(1+2+6+7+12+11+7+1)=3.
(2)解:
由样本数据可知“优秀”档次所占的百分比为=8%,
∴,估计九年级400名学生中为优秀档次的人数为400×8%=32
(3)解:用A、B、C表示阅读本数是8的学生,用D表示阅读9本的学生,列表得到:
A B C D
A AB AC AD
B BA BC BD
C CA CB CD
D DA DB DC
由列表可知,共12种等可能的结果,其中所抽取的2名学生中有1名阅读本数为9的有6种,所以抽取的2名学生中有1名阅读本数为9的概率为
【知识点】用样本估计总体;扇形统计图;用列表法或树状图法求概率
18.【答案】(1)64
(2)解:选择平均数,
由表可知,去年“声呐鲟”到达下游监测点的平均时间为64.2小时,而今年“声呐鲟”到达下游监测点的平均时间为56.2小时,缩短了8小时,
所以今年“声呐鲟”从长江到海洋的适应情况更好(答案不唯一,合理即可).
(3)解:1300×(尾).
答:其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有624尾中华鲟通过监测站A.
【知识点】用样本估计总体;频数(率)分布直方图;扇形统计图;分析数据的集中趋势(平均数、中位数、众数)
19.【答案】(1)68;23%
(2)320
(3)解:①小胡的说法正确,理由如下:
初中生的视力众数是1.0,高中生的视力众数是0.9,
1.0>0.9
初中学生的视力水平比高中学生的好;(理由不唯一)
②方法一:(名);
方法二:14300(名).
答:该区大约有14300名中学生视力不良.
对视力保护提出的建议是:坚持做眼保健操,加强体育锻炼,养成良好的阅读习惯,保护个人视力.(答案不唯一,合理即可)
【知识点】总体、个体、样本、样本容量;用样本估计总体;频数(率)分布表;频数(率)分布直方图;统计表;条形统计图
21世纪教育网(www.21cnjy.com)
2 / 11
