华师大版数学九年级下册综合题一(含答案)
文档属性
| 名称 | 华师大版数学九年级下册综合题一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1019.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 06:39:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
华师大版数学九年级下册综合题一
一、单选题
1.如图,已知,为上一点,以为半径的圆经过点,且与、交于点、,设,,则( )
A.若,则弧的度数为
B.若,则弧的度数为
C.若,则弧的度数为
D.若,则弧的度数为
2.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m,,则弯道外边缘的长为( )
A. B. C. D.
3.下列调查中,最适合采用全面调查的是( )
A.调查我国初中生的周末阅读时间
B.调查“神舟十五号”飞船各零部件的合格情况
C.调查某品牌汽车的抗撞击能力
D.调查巢湖的水质情况
4.在平面直角坐标系中,将抛物线y=2x2-4先向右平移2个单位长度,再向上平移1个单位长度得到的拋物线对应的函数表达式是( )
A.y=2(x+2)2+3 B.y=2(x+2)2-3 C.y=2(x-2)2+3 D.y=2(x-2)2-3
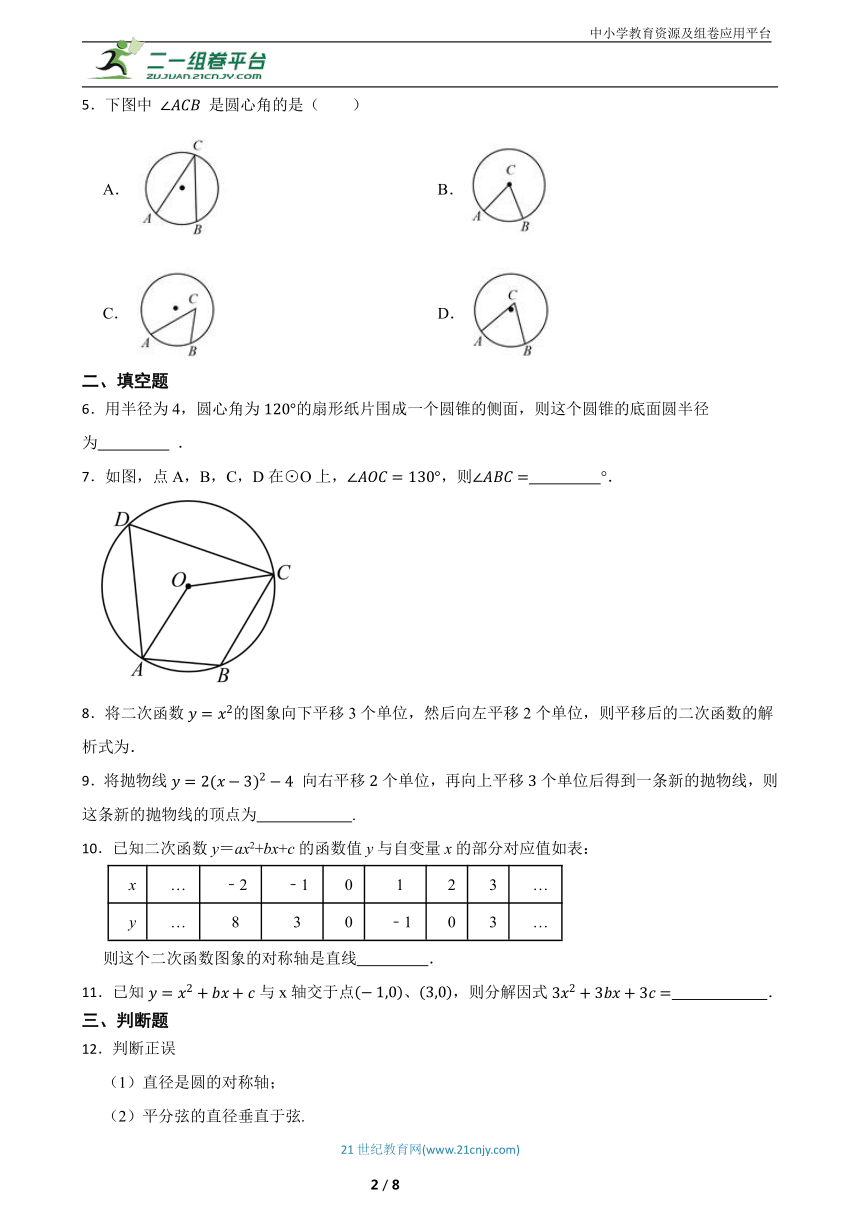
5.下图中 是圆心角的是( )
A. B.
C. D.
二、填空题
6.用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为 .
7.如图,点A,B,C,D在⊙O上,,则 °.
8.将二次函数的图象向下平移3个单位,然后向左平移2个单位,则平移后的二次函数的解析式为.
9.将抛物线 向右平移个单位,再向上平移个单位后得到一条新的抛物线,则这条新的抛物线的顶点为 .
10.已知二次函数y=ax2+bx+c的函数值y与自变量x的部分对应值如表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 8 3 0 ﹣1 0 3 …
则这个二次函数图象的对称轴是直线 .
11.已知与x轴交于点、,则分解因式 .
三、判断题
12.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
13.圆的周长是直径的 π 倍.(判断对错)
四、计算题
14.已知抛物线的顶点是,与y轴交于点,求该抛物线的解析式.
15.已知抛物线的顶点为,且在抛物线上,求抛物线的解析式.
五、解答题
16.脱贫攻坚的收官之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于60元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如表所示.
销售单价x(元) 30 40 45
销售数量y(件) 100 80 70
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式.
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少元?
17.如图在平面直角坐标系xOy中,二次函数的图象与x轴、y轴的交点分别为(1,0)和.
(1)求此二次函数的表达式;
(2)结合函数图象,直接写出当时,x的取值范围.
六、综合题
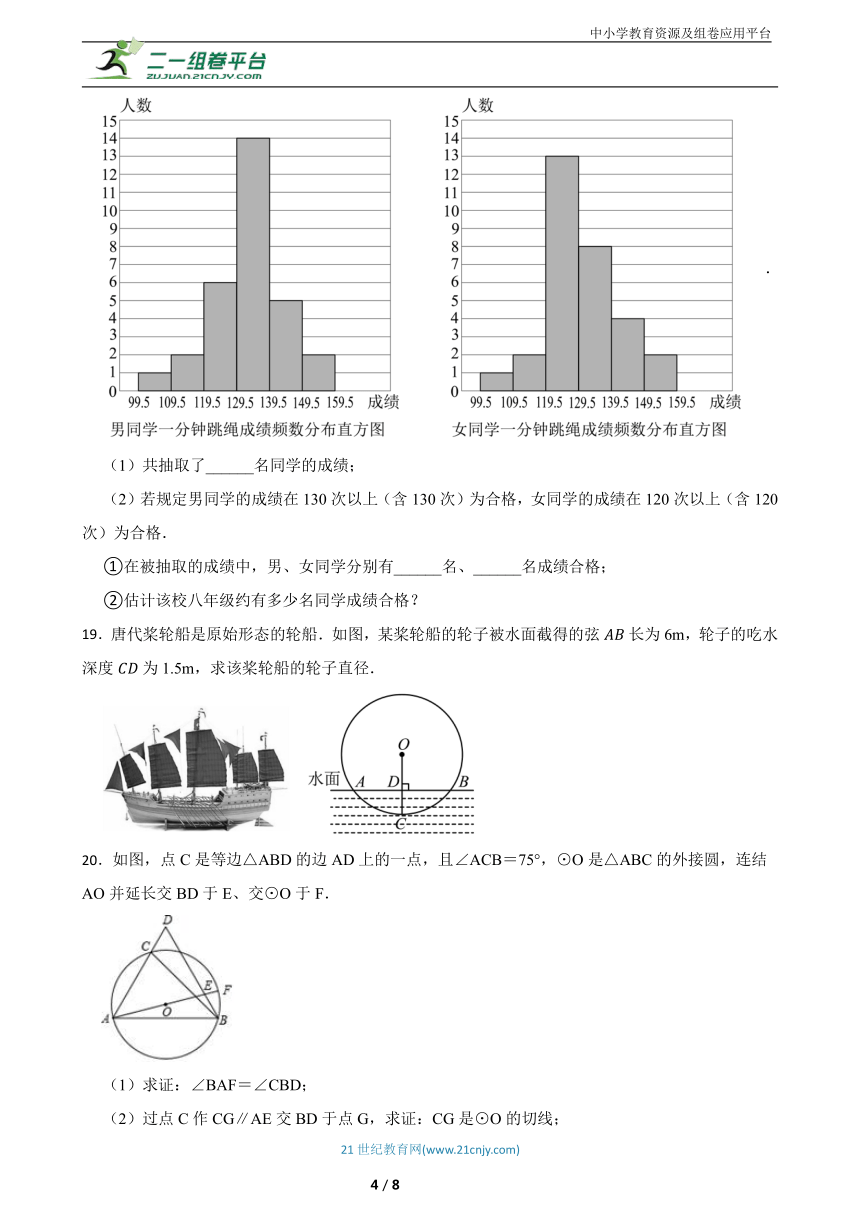
18.为积极响应市领导倡导的“阳光体育运动”的号召,某校八年级全体同学参加了一分钟跳绳比赛.八年级共有600名同学(其中女同学320名),从中随机抽取部分同学的成绩,绘制频数分布直方图如图.
.
(1)共抽取了______名同学的成绩;
(2)若规定男同学的成绩在130次以上(含130次)为合格,女同学的成绩在120次以上(含120次)为合格.
①在被抽取的成绩中,男、女同学分别有______名、______名成绩合格;
②估计该校八年级约有多少名同学成绩合格?
19.唐代桨轮船是原始形态的轮船.如图,某桨轮船的轮子被水面截得的弦长为6m,轮子的吃水深度为1.5m,求该桨轮船的轮子直径.
20.如图,点C是等边△ABD的边AD上的一点,且∠ACB=75°,⊙O是△ABC的外接圆,连结AO并延长交BD于E、交⊙O于F.
(1)求证:∠BAF=∠CBD;
(2)过点C作CG∥AE交BD于点G,求证:CG是⊙O的切线;
(3)在(2)的条件下,当AF=2 时,求 的值.
七、实践探究题
21.综合与探究
如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.已知,,点P是第一象限抛物线上对称轴右侧的一个动点,设点P的横坐标为m.
(1)求抛物线的函数表达式,并直接写出点C,D的坐标;
(2)连接,求面积的最大值.
答案解析部分
1.【答案】B
【知识点】三角形的外角性质;圆周角定理
2.【答案】C
【知识点】弧长的计算
3.【答案】B
【知识点】全面调查与抽样调查
4.【答案】D
【知识点】二次函数图象的几何变换
5.【答案】B
【知识点】圆心角、弧、弦的关系
6.【答案】
【知识点】圆锥的计算
7.【答案】115
【知识点】圆周角定理;圆内接四边形的性质
8.【答案】
【知识点】二次函数图象的几何变换
9.【答案】(5,-1)
【知识点】二次函数图象的几何变换
10.【答案】x=1
【知识点】二次函数y=ax²+bx+c的性质
11.【答案】
【知识点】因式分解法解一元二次方程;二次函数图象与坐标轴的交点问题
12.【答案】(1)正确
(2)错误
【知识点】垂径定理
13.【答案】正确
【知识点】圆的相关概念
14.【答案】
【知识点】待定系数法求二次函数解析式
15.【答案】
【知识点】待定系数法求二次函数解析式
16.【答案】(1)y=-2x+160;
(2)销售单价定为55元时,该商品每天获得的利润最大,最大利润是1250元
【知识点】二元一次方程组的实际应用-销售问题;二次函数的实际应用-销售问题
17.【答案】(1)
(2)或
【知识点】待定系数法求二次函数解析式
18.【答案】(1)60
(2)①21,27;②484名
【知识点】频数(率)分布直方图;用样本所占百分比估计总体数量
19.【答案】该桨轮船的轮子直径为
【知识点】勾股定理;垂径定理
20.【答案】(1)解:如图,连接CF.
∵AF为直径,
∴∠ACF=90°,
∵∠ACB=75°,
∴∠BCF=90°﹣75°=15°,
∴∠BAF=15°,
∵△ABD为等边三角形,
∴∠D=∠DAB=∠DBA=60°,
∴∠CBD=∠ACB﹣∠D=75°﹣60°=15°,
∴∠BAF=∠CBD
(2)解:过点C作CG∥AE交BD于点G,连接CO,
∵∠CAF=∠CAB﹣∠BAF=60°﹣15°=45°,
∠ACF=90°,
∴∠CFA=45°,
∴CA=CF,
∴CO⊥AF,
∵CG∥AE,
∴CO⊥CG,
∴CG是⊙O的切线
(3)解:作CH⊥AB于H,
∵AF= ,
∴AC=CF= AF=2,
在△ACB中,
∠CAB=60°,∠ACB=75°,∠ABC=45°,
∴∠ACH=30°,∠HCB=∠HBC=45°,
∴AH= AC=1,CH= ,AH= ,BH=CH= ,
∴AB=AH+BH=1+ ,
∴AD=AB= ,CD=AD﹣AC=
∵CG∥AE,
∴∠DCG=∠CAF=45°,
在△DCG与△ABC中,
∠DCG=∠ABC=45°,∠D=∠CAB=60°,
∴△DCG∽△ABC,
∴ ,
∴ 的值为 .
【知识点】等边三角形的性质;切线的判定
21.【答案】(1)抛物线的函数表达式为,点C的坐标为,点D的坐标为;
(2)面积的最大值为.
【知识点】待定系数法求二次函数解析式;二次函数-面积问题
21世纪教育网(www.21cnjy.com)
2 / 8
华师大版数学九年级下册综合题一
一、单选题
1.如图,已知,为上一点,以为半径的圆经过点,且与、交于点、,设,,则( )
A.若,则弧的度数为
B.若,则弧的度数为
C.若,则弧的度数为
D.若,则弧的度数为
2.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m,,则弯道外边缘的长为( )
A. B. C. D.
3.下列调查中,最适合采用全面调查的是( )
A.调查我国初中生的周末阅读时间
B.调查“神舟十五号”飞船各零部件的合格情况
C.调查某品牌汽车的抗撞击能力
D.调查巢湖的水质情况
4.在平面直角坐标系中,将抛物线y=2x2-4先向右平移2个单位长度,再向上平移1个单位长度得到的拋物线对应的函数表达式是( )
A.y=2(x+2)2+3 B.y=2(x+2)2-3 C.y=2(x-2)2+3 D.y=2(x-2)2-3
5.下图中 是圆心角的是( )
A. B.
C. D.
二、填空题
6.用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为 .
7.如图,点A,B,C,D在⊙O上,,则 °.
8.将二次函数的图象向下平移3个单位,然后向左平移2个单位,则平移后的二次函数的解析式为.
9.将抛物线 向右平移个单位,再向上平移个单位后得到一条新的抛物线,则这条新的抛物线的顶点为 .
10.已知二次函数y=ax2+bx+c的函数值y与自变量x的部分对应值如表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 8 3 0 ﹣1 0 3 …
则这个二次函数图象的对称轴是直线 .
11.已知与x轴交于点、,则分解因式 .
三、判断题
12.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
13.圆的周长是直径的 π 倍.(判断对错)
四、计算题
14.已知抛物线的顶点是,与y轴交于点,求该抛物线的解析式.
15.已知抛物线的顶点为,且在抛物线上,求抛物线的解析式.
五、解答题
16.脱贫攻坚的收官之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于60元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如表所示.
销售单价x(元) 30 40 45
销售数量y(件) 100 80 70
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式.
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少元?
17.如图在平面直角坐标系xOy中,二次函数的图象与x轴、y轴的交点分别为(1,0)和.
(1)求此二次函数的表达式;
(2)结合函数图象,直接写出当时,x的取值范围.
六、综合题
18.为积极响应市领导倡导的“阳光体育运动”的号召,某校八年级全体同学参加了一分钟跳绳比赛.八年级共有600名同学(其中女同学320名),从中随机抽取部分同学的成绩,绘制频数分布直方图如图.
.
(1)共抽取了______名同学的成绩;
(2)若规定男同学的成绩在130次以上(含130次)为合格,女同学的成绩在120次以上(含120次)为合格.
①在被抽取的成绩中,男、女同学分别有______名、______名成绩合格;
②估计该校八年级约有多少名同学成绩合格?
19.唐代桨轮船是原始形态的轮船.如图,某桨轮船的轮子被水面截得的弦长为6m,轮子的吃水深度为1.5m,求该桨轮船的轮子直径.
20.如图,点C是等边△ABD的边AD上的一点,且∠ACB=75°,⊙O是△ABC的外接圆,连结AO并延长交BD于E、交⊙O于F.
(1)求证:∠BAF=∠CBD;
(2)过点C作CG∥AE交BD于点G,求证:CG是⊙O的切线;
(3)在(2)的条件下,当AF=2 时,求 的值.
七、实践探究题
21.综合与探究
如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.已知,,点P是第一象限抛物线上对称轴右侧的一个动点,设点P的横坐标为m.
(1)求抛物线的函数表达式,并直接写出点C,D的坐标;
(2)连接,求面积的最大值.
答案解析部分
1.【答案】B
【知识点】三角形的外角性质;圆周角定理
2.【答案】C
【知识点】弧长的计算
3.【答案】B
【知识点】全面调查与抽样调查
4.【答案】D
【知识点】二次函数图象的几何变换
5.【答案】B
【知识点】圆心角、弧、弦的关系
6.【答案】
【知识点】圆锥的计算
7.【答案】115
【知识点】圆周角定理;圆内接四边形的性质
8.【答案】
【知识点】二次函数图象的几何变换
9.【答案】(5,-1)
【知识点】二次函数图象的几何变换
10.【答案】x=1
【知识点】二次函数y=ax²+bx+c的性质
11.【答案】
【知识点】因式分解法解一元二次方程;二次函数图象与坐标轴的交点问题
12.【答案】(1)正确
(2)错误
【知识点】垂径定理
13.【答案】正确
【知识点】圆的相关概念
14.【答案】
【知识点】待定系数法求二次函数解析式
15.【答案】
【知识点】待定系数法求二次函数解析式
16.【答案】(1)y=-2x+160;
(2)销售单价定为55元时,该商品每天获得的利润最大,最大利润是1250元
【知识点】二元一次方程组的实际应用-销售问题;二次函数的实际应用-销售问题
17.【答案】(1)
(2)或
【知识点】待定系数法求二次函数解析式
18.【答案】(1)60
(2)①21,27;②484名
【知识点】频数(率)分布直方图;用样本所占百分比估计总体数量
19.【答案】该桨轮船的轮子直径为
【知识点】勾股定理;垂径定理
20.【答案】(1)解:如图,连接CF.
∵AF为直径,
∴∠ACF=90°,
∵∠ACB=75°,
∴∠BCF=90°﹣75°=15°,
∴∠BAF=15°,
∵△ABD为等边三角形,
∴∠D=∠DAB=∠DBA=60°,
∴∠CBD=∠ACB﹣∠D=75°﹣60°=15°,
∴∠BAF=∠CBD
(2)解:过点C作CG∥AE交BD于点G,连接CO,
∵∠CAF=∠CAB﹣∠BAF=60°﹣15°=45°,
∠ACF=90°,
∴∠CFA=45°,
∴CA=CF,
∴CO⊥AF,
∵CG∥AE,
∴CO⊥CG,
∴CG是⊙O的切线
(3)解:作CH⊥AB于H,
∵AF= ,
∴AC=CF= AF=2,
在△ACB中,
∠CAB=60°,∠ACB=75°,∠ABC=45°,
∴∠ACH=30°,∠HCB=∠HBC=45°,
∴AH= AC=1,CH= ,AH= ,BH=CH= ,
∴AB=AH+BH=1+ ,
∴AD=AB= ,CD=AD﹣AC=
∵CG∥AE,
∴∠DCG=∠CAF=45°,
在△DCG与△ABC中,
∠DCG=∠ABC=45°,∠D=∠CAB=60°,
∴△DCG∽△ABC,
∴ ,
∴ 的值为 .
【知识点】等边三角形的性质;切线的判定
21.【答案】(1)抛物线的函数表达式为,点C的坐标为,点D的坐标为;
(2)面积的最大值为.
【知识点】待定系数法求二次函数解析式;二次函数-面积问题
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
