4-3-2对数的运算 课件(共32张PPT)-高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 4-3-2对数的运算 课件(共32张PPT)-高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
4.3.2 对 数 的 运 算
第四章 指数函数与对数函数
学习目标
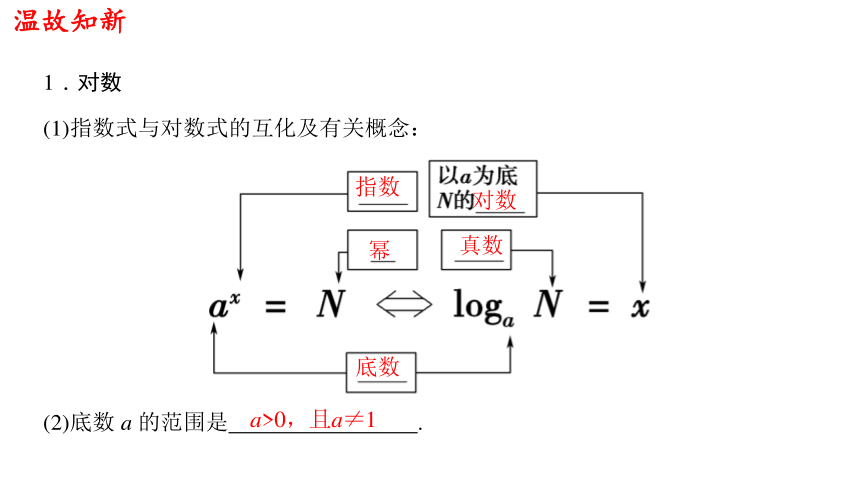
温故知新
在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究?
提出问题
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
1.对数的运算性质
探究一:
化为对数式,
它们之间有何关系?
结合指数的运算性质能否将
化为对数式?
将指数式
问题探究
试一试:由
得:
由
得
从而得出
探究二:结合前面的推导,由指数式
又能得到什么样的结论?
试一试:由
得
问题探究
又能得到什么样的结论?
试一试:由
得
探究三:结合前面的推导,由指数式
问题探究
对数的运算法则
思考辨析
典例解析
跟踪训练
归纳总结
探究四:结合对数的定义,你能推导出对数的换底公式吗
(a>0,且a≠1; c>0,且c≠1; b>0)
问题探究
数学史上,人们经过大量的努力,制作了常用对数表和自然对数表,只有通过查表就能求出任意正数的常用对数或自然对数。现在,利用计算器,也可以直接求出任意正数的常用对数或自然对数。这样,如果能将其他底的对数转换为以10或e为底的对数,就能方便地求出这些对数。
换底公式
证明:设
由对数的定义可以得:
即证得
这个公式叫做换底公式,一般取常用对数进行换底
问题探究
在4.2.1的问题1中,求经过多少年B地景区的游客人次是2001年的2倍,就是计算 2 的值。
由换底公式可得2=,
利用计算工具,可得=,
由此可得,大约经过7年,B地景区的
游客人次就达到2001年的2倍,类似地,
可以求出游客人次是2001年的3倍,4倍,
…所需要的年数。
2011年3月11日,日本东北部海域发生里氏9.0级地震,
它所释放出来的能量是2008年5月12日我国汶川
发生里氏8.0级地震的多少倍(精确到1)?
例3.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震M之间的关系为
典例解析
解:设里氏9.0级和里氏8.0级地震的能量分别为E1和E2
设里利用计算工具可得,
虽然里氏9.0级和里氏8.0级地震仅相差1级,但前者释放出的能量却是后者的约32倍。
跟踪训练
跟踪训练
归纳总结
当堂达标
1.对数的运算法则。
2.利用定义及指数运算证明对数的运算法则。
3.对数运算法则的应用。
4.换底公式的证明及应用。
课堂小结
积、商、幂的对数运算法则:
如果a>0,a 1,M>0,N>0,那么:
(a>0,且a≠1; c>0,且c≠1;
4.3.2 对 数 的 运 算
第四章 指数函数与对数函数
学习目标
温故知新
在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究?
提出问题
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
1.对数的运算性质
探究一:
化为对数式,
它们之间有何关系?
结合指数的运算性质能否将
化为对数式?
将指数式
问题探究
试一试:由
得:
由
得
从而得出
探究二:结合前面的推导,由指数式
又能得到什么样的结论?
试一试:由
得
问题探究
又能得到什么样的结论?
试一试:由
得
探究三:结合前面的推导,由指数式
问题探究
对数的运算法则
思考辨析
典例解析
跟踪训练
归纳总结
探究四:结合对数的定义,你能推导出对数的换底公式吗
(a>0,且a≠1; c>0,且c≠1; b>0)
问题探究
数学史上,人们经过大量的努力,制作了常用对数表和自然对数表,只有通过查表就能求出任意正数的常用对数或自然对数。现在,利用计算器,也可以直接求出任意正数的常用对数或自然对数。这样,如果能将其他底的对数转换为以10或e为底的对数,就能方便地求出这些对数。
换底公式
证明:设
由对数的定义可以得:
即证得
这个公式叫做换底公式,一般取常用对数进行换底
问题探究
在4.2.1的问题1中,求经过多少年B地景区的游客人次是2001年的2倍,就是计算 2 的值。
由换底公式可得2=,
利用计算工具,可得=,
由此可得,大约经过7年,B地景区的
游客人次就达到2001年的2倍,类似地,
可以求出游客人次是2001年的3倍,4倍,
…所需要的年数。
2011年3月11日,日本东北部海域发生里氏9.0级地震,
它所释放出来的能量是2008年5月12日我国汶川
发生里氏8.0级地震的多少倍(精确到1)?
例3.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震M之间的关系为
典例解析
解:设里氏9.0级和里氏8.0级地震的能量分别为E1和E2
设里利用计算工具可得,
虽然里氏9.0级和里氏8.0级地震仅相差1级,但前者释放出的能量却是后者的约32倍。
跟踪训练
跟踪训练
归纳总结
当堂达标
1.对数的运算法则。
2.利用定义及指数运算证明对数的运算法则。
3.对数运算法则的应用。
4.换底公式的证明及应用。
课堂小结
积、商、幂的对数运算法则:
如果a>0,a 1,M>0,N>0,那么:
(a>0,且a≠1; c>0,且c≠1;
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
