5.5用二次函数解决问题（含答案）

中小学教育资源及组卷应用平台
5.5用二次函数解决问题
一、单选题
1．一辆新汽车原价 万元，如果每年折旧率为 ，两年后这辆汽车的价钱为 元，则 关于 的函数关系式为（　　）
A．y=20(1+x)2 B．y=20(1-x)2 C．y=20(1+x) D．y=20+x2
2．教练对小明推铅球的录像进行技术分析，发现某次铅球行进高度与水平距离之间的关系为；由此可知小明这次的推铅球成绩是（　　）
A． B． C． D．
3．某广场有一喷水池，水从地面喷出.如图所示，以水平地面为轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线(单位：)的一部分，则水喷出的最大高度是（　　）。
A． B． C． D．
4．某航模组设计的火箭模型的升空高度与点火后飞行时间满足函数表达式．则点火后该火箭模型的升空高度为（　　）
A．53 B．47 C．45 D．44
5．如图，铅球运动员掷铅球的高度与水平距离之间的函数关系式是，则该运动员此次掷铅球的成绩是（　　）
A． B． C． D．
6．烟花厂为成都春节特别设计制作一种新型礼炮，这种礼炮的升空高度h（m）与飞行时间t（s）的关系式是 ，若这种礼炮在点火升空到最高点引爆，则从点火升空到引爆需要的时间为（　　）
A．3s B．4s C．5s D．6s
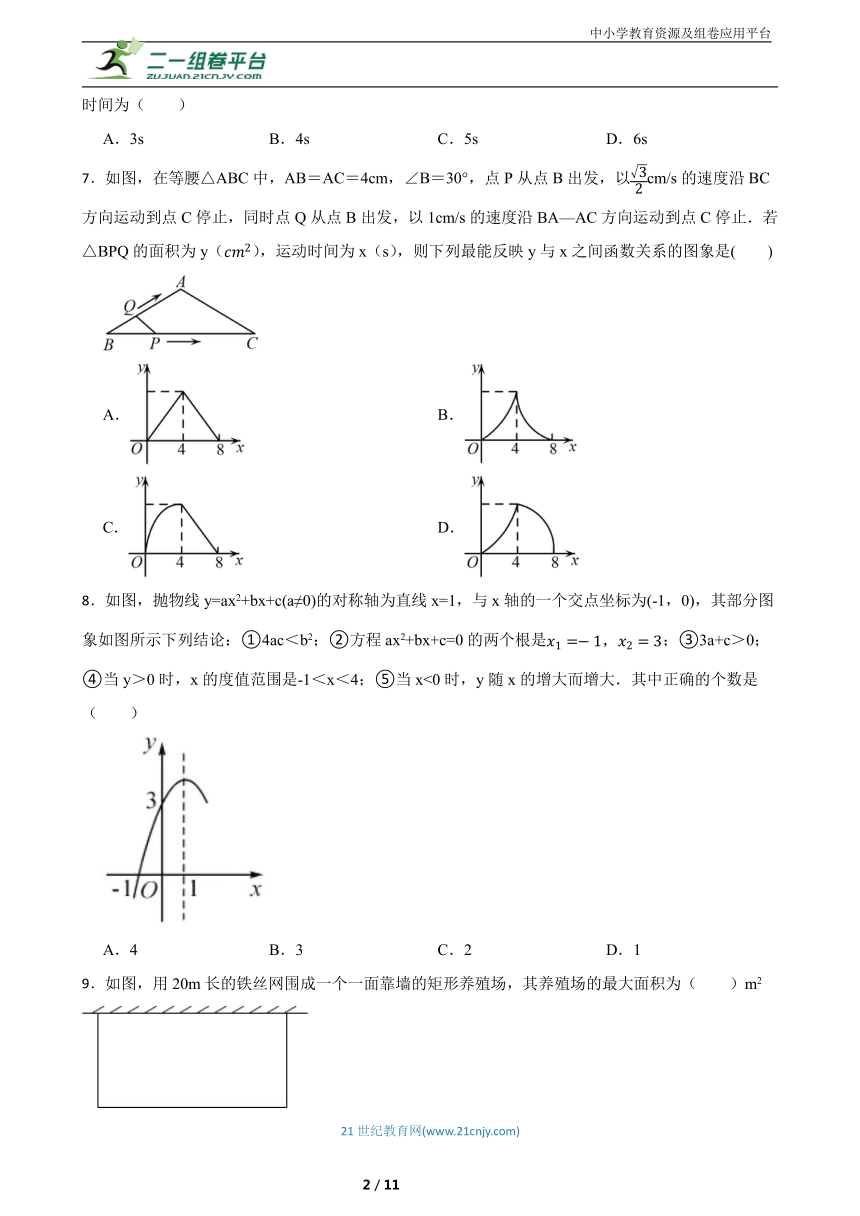
7．如图，在等腰△ABC中，AB＝AC＝4cm，∠B＝30°，点P从点B出发，以cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA—AC方向运动到点C停止．若△BPQ的面积为y（），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是(　　)
A． B．
C． D．
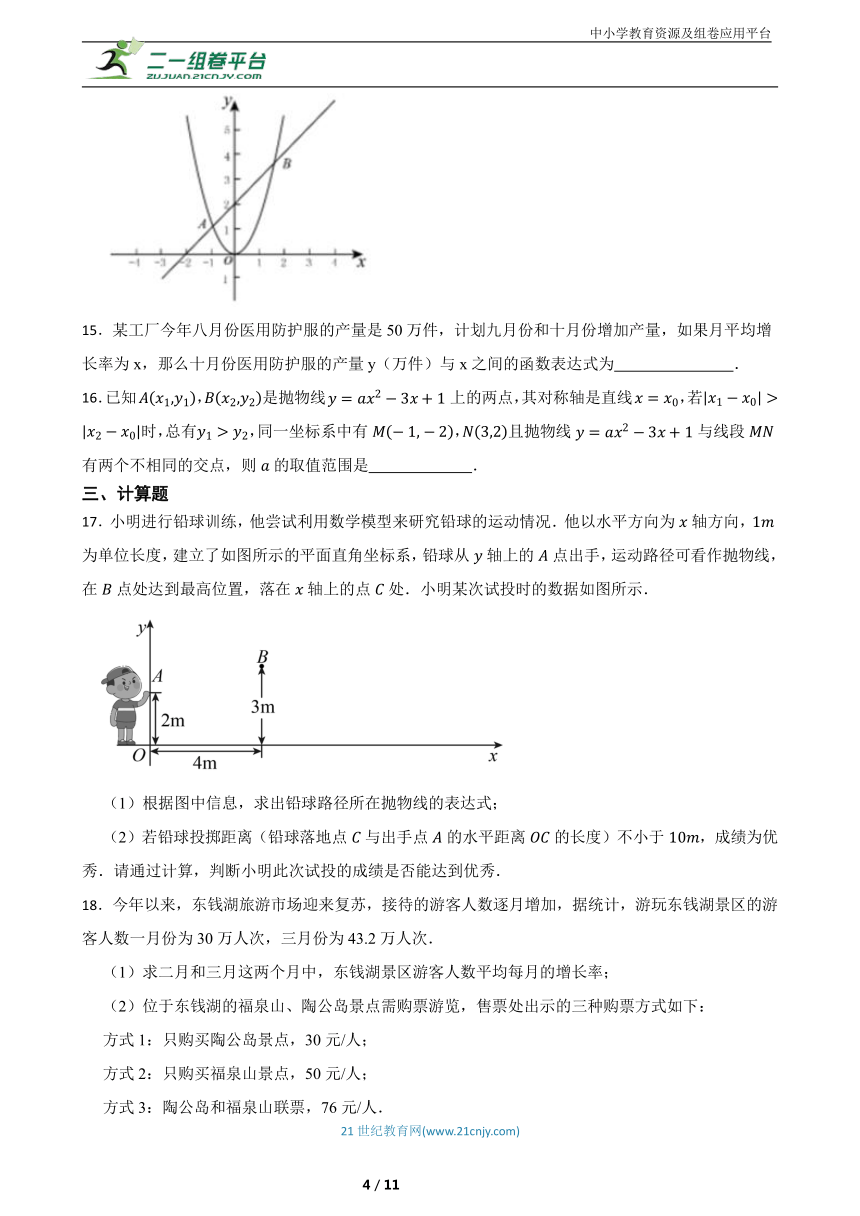
8．如图，抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1，与x轴的一个交点坐标为(-1，0)，其部分图象如图所示下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是；③3a+c＞0；④当y＞0时，x的度值范围是-1＜x＜4；⑤当x<0时，y随x的增大而增大．其中正确的个数是（　　）
A．4 B．3 C．2 D．1
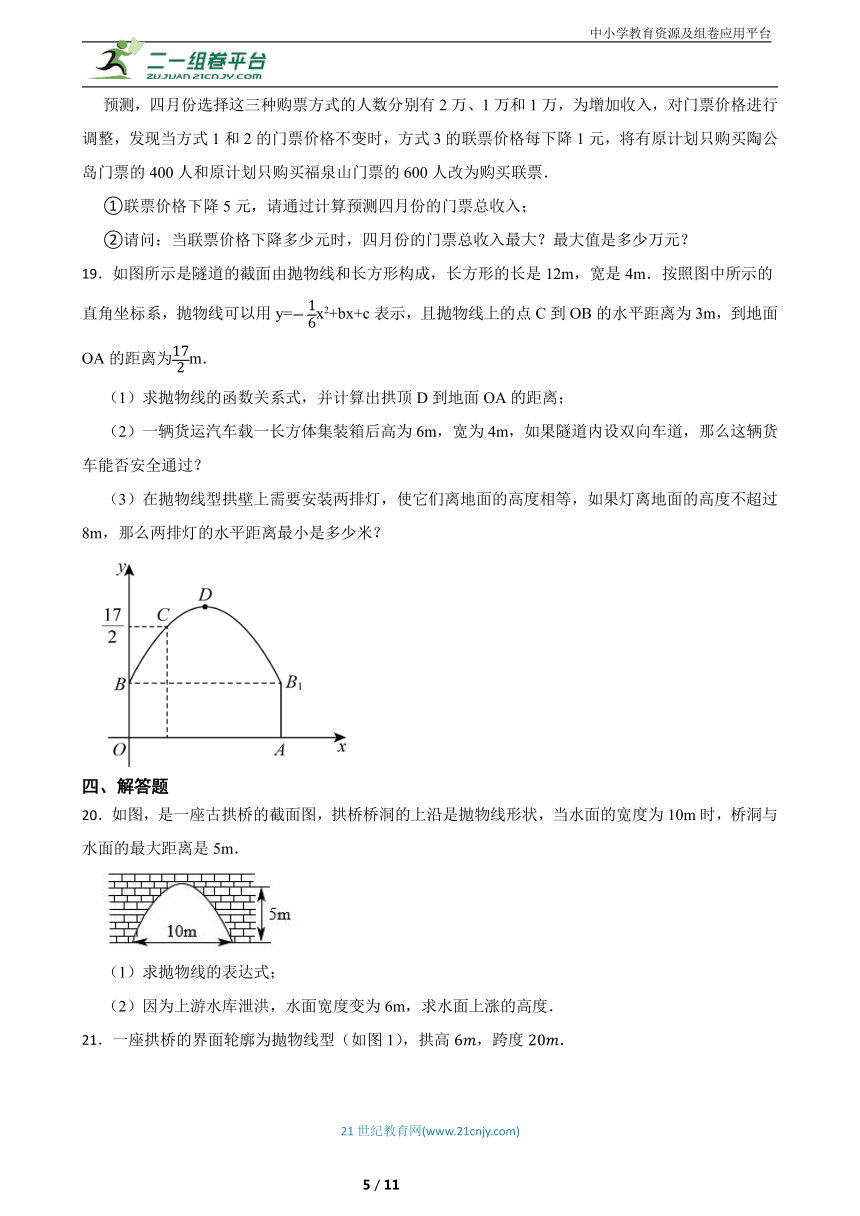
9．如图，用20m长的铁丝网围成一个一面靠墙的矩形养殖场，其养殖场的最大面积为（　　）m2
A．45 B．50 C．60 D．65
10．已知二次函数下列结论正确的是（　　）
①已知点，点在二次函数的图象上，则；②该图象一定过定点和；③直线与抛物线一定存在两个交点；④当时，的最小值是，则．
A．①②③ B．①③④ C．②③④ D．①②③④
二、填空题
11．如图，桥洞的拱形是抛物线，其顶部离水面的距离为，水面宽为，以水平向右方向为轴的正方向，建立平面直角坐标系，当点为原点时，抛物线表达式是，若选取点为坐标原点，则抛物线的表达式为 　 　．
12．要修建一个圆形喷水池在池中心竖直安装一根水管，在水管的顶端安一个喷水头使喷出的抛物线形水柱在与处达到最高，高度，水柱落地处离池中心，应安装水管的长度是　 　．
13．如图，用一段长为30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m，当平行于墙面的边长为　 　m时，菜园的面积最大．
14．如图，抛物线 与直线 的两个交点坐标分别为 ， ，则使得关于 的不等式 成立的 的取值范围是　 　.
15．某工厂今年八月份医用防护服的产量是50万件，计划九月份和十月份增加产量，如果月平均增长率为x，那么十月份医用防护服的产量y（万件）与x之间的函数表达式为　 　．
16．已知，是抛物线上的两点，其对称轴是直线，若时，总有，同一坐标系中有，且抛物线与线段有两个不相同的交点，则的取值范围是　 　．
三、计算题
17．小明进行铅球训练，他尝试利用数学模型来研究铅球的运动情况．他以水平方向为轴方向，为单位长度，建立了如图所示的平面直角坐标系，铅球从轴上的点出手，运动路径可看作抛物线，在点处达到最高位置，落在轴上的点处．小明某次试投时的数据如图所示．
（1）根据图中信息，求出铅球路径所在抛物线的表达式；
（2）若铅球投掷距离（铅球落地点与出手点的水平距离的长度）不小于，成绩为优秀．请通过计算，判断小明此次试投的成绩是否能达到优秀．
18．今年以来，东钱湖旅游市场迎来复苏，接待的游客人数逐月增加，据统计，游玩东钱湖景区的游客人数一月份为30万人次，三月份为43.2万人次．
（1）求二月和三月这两个月中，东钱湖景区游客人数平均每月的增长率；
（2）位于东钱湖的福泉山、陶公岛景点需购票游览，售票处出示的三种购票方式如下：
方式1：只购买陶公岛景点，30元/人；
方式2：只购买福泉山景点，50元/人；
方式3：陶公岛和福泉山联票，76元/人．
预测，四月份选择这三种购票方式的人数分别有2万、1万和1万，为增加收入，对门票价格进行调整，发现当方式1和2的门票价格不变时，方式3的联票价格每下降1元，将有原计划只购买陶公岛门票的400人和原计划只购买福泉山门票的600人改为购买联票．
①联票价格下降5元，请通过计算预测四月份的门票总收入；
②请问：当联票价格下降多少元时，四月份的门票总收入最大？最大值是多少万元？
19．如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=x2+bx+c表示，且抛物线上的点C到OB的水平距离为3m，到地面OA的距离为m．
（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？
四、解答题
20．如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．
（1）求抛物线的表达式；
（2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
21．一座拱桥的界面轮廓为抛物线型（如图1），拱高，跨度．
（1）将抛物线放在所给的直角坐标系中（如图2），其表达式是的形式，请根据所给的数据求出该抛物线表达式．
（2）拱桥下地平面是双向行车道（正中间隔离带宽度不计），其中的一条行车道要能并排行驶三辆宽的汽车（汽车间的间隔忽略不计），则在最外侧车道上的汽车最高为多少米？
22．善于不断改进学习方法的小迪发现，对解题进行回顾反思，学习效果更好．某一天小迪有20分钟时间可用于学习．假设小迪用于解题的时间x（单位：分钟）与学习收益量y的关系如图1所示，用于回顾反思的时间x（单位：分钟）与学习收益y的关系如图2所示（其中OA是抛物线的一部分，A为抛物线的顶点），且用于回顾反思的时间不超过用于解题的时间．
（1）求小迪解题的学习收益量y与用于解题的时间x之间的函数关系式；
（2）求小迪回顾反思的学习收益量y与用于回顾反思的时间x的函数关系式；
（3）问小迪如何分配解题和回顾反思的时间，才能使这20分钟的学习收益总量最大？
23．如图，直线y=x+4与x轴，y轴分别交于点A，B．抛物线L：y=-x2+bx+3c经过点A，L与线段AB的另一个交点为点C（不与点B重合），P（m，n） 为抛物线上点A、C之间的一动点
（1）点A的坐标为　 　，点B的坐标为　 　
（2）求b，c的数量关系：
（3）若L经过OB的中点，
①求L的解析式：
②求点P到AB距离的最大值．
答案解析部分
1．【答案】B
【知识点】二次函数的实际应用-百分率问题
2．【答案】C
【知识点】二次函数的实际应用-抛球问题
3．【答案】A
【知识点】二次函数的实际应用-喷水问题
4．【答案】C
【知识点】二次函数的实际应用-抛球问题
5．【答案】D
【知识点】二次函数的实际应用-抛球问题
6．【答案】B
【知识点】二次函数的其他应用
7．【答案】D
【知识点】二次函数-动态几何问题
8．【答案】B
【知识点】二次函数图象与系数的关系；二次函数的其他应用
9．【答案】B
【知识点】二次函数的实际应用-几何问题
10．【答案】A
【知识点】二次函数图象与系数的关系；二次函数与一次函数的综合应用；二次函数图象上点的坐标特征
11．【答案】
【知识点】二次函数的实际应用-拱桥问题
12．【答案】
【知识点】二次函数的实际应用-喷水问题
13．【答案】15
【知识点】二次函数的实际应用-几何问题
14．【答案】-1＜x＜2
【知识点】二次函数与一次函数的综合应用
15．【答案】
【知识点】二次函数的实际应用-百分率问题
16．【答案】
【知识点】一元二次方程根的判别式及应用；二次函数-动态几何问题
17．【答案】（1）
（2）能达到优秀
【知识点】待定系数法求二次函数解析式；二次函数的实际应用-抛球问题
18．【答案】（1）每月的增长率为20%；
（2）①四月份的门票总收入为195.5（万元）；②当联票价格下降12元时，四月份的门票总收入最大，最大值是200.4万元
【知识点】一元二次方程的实际应用-百分率问题；二次函数的实际应用-销售问题
19．【答案】解：（1）由题知点在抛物线上，
得，
解得，
∴，
∴当时，
∴抛物线解析式为，拱顶D到地面OA的距离为10米；
（2）可以通过，理由如下：
由题知车最外侧与地面OA的交点为（2，0）或（10，0）
当x=2或x=10时，，
所以可以通过；
（3）令，即，
可得，
解得
答：两排灯的水平距离最小是.
【知识点】二次函数的实际应用-拱桥问题
20．【答案】（1）
（2）水面上涨的高度为m
【知识点】待定系数法求二次函数解析式；二次函数的实际应用-拱桥问题
21．【答案】（1）
（2）3.84米
【知识点】待定系数法求二次函数解析式；二次函数的实际应用-拱桥问题
22．【答案】解：（1）由图1，设y=kx（k≠0）．当x=1时，y=2，解得k=2∴y=2x（0≤x≤20）（2）中的收益量y与反思时间x的函数关系必须分段：由图2，当0≤x＜4时，设y=a（x﹣4）2+16（a≠0），由已知，当x=0时，y=0∴0=16a+16，∴a=﹣1∴y=﹣（x﹣4）2+16即y=﹣x2+8x当4≤x≤10时，y=16．因此，函数关系式为：当0≤x＜4时，y=﹣（x﹣4）2+16；当4≤x≤10时，y=16．（3）设小迪用于回顾反思的时间为x（0≤x≤10）分钟，学习收益总量为y，则她用于解题的时间为（20﹣x）分钟．当0≤x＜4时，y=﹣x2+8x+2（20﹣x）=﹣（x﹣3）2+49∵a=﹣1＜0∴函数有最大值，当x=3时，有最大值49；当4≤x≤10时，y=16+2（20﹣x）=56﹣2x，y随x的增大而减小，因此当x=4时，有最大值48．综合以上，当x=3时，有最大值49，此时20﹣x=17．即小迪用于回顾反思的时间为3分钟，用于解题的时间为17分钟时，学习的总收益量最大．
【知识点】二次函数的实际应用-销售问题
23．【答案】（1）（3， 0）；（0， 4）
（2）解：把A（3，0）代入y= -x2+bx+3c得
-9+3b+3c= 0，
整理得b+c=3
（3）解：①由题知OB中点（0，2）， 代入y= -x2+bx+3c得
3c=2，解得c=
又b+c=3，
∴b=
L的抛物线解析式为y=-x2+x+2．
②由题知，
解得或者
∴（，），
设P（m， -m2+m+ 2）（ ∵A（3，0）， B（0， 4），
∴AB== 5，
连接BP，AP， OP，
∵S△PAB =S△PBO+S△PAO-S△OAB，
∴．
∴h=
∴当m=时，h的最大值时
∴点P到AB距离的最大值为
【知识点】二次函数与一次函数的综合应用；二次函数-动态几何问题
21世纪教育网(www.21cnjy.com)
2 / 11