6.4探索三角形相似的条件(含答案)
文档属性
| 名称 | 6.4探索三角形相似的条件(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 535.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-01 00:00:00 | ||
图片预览


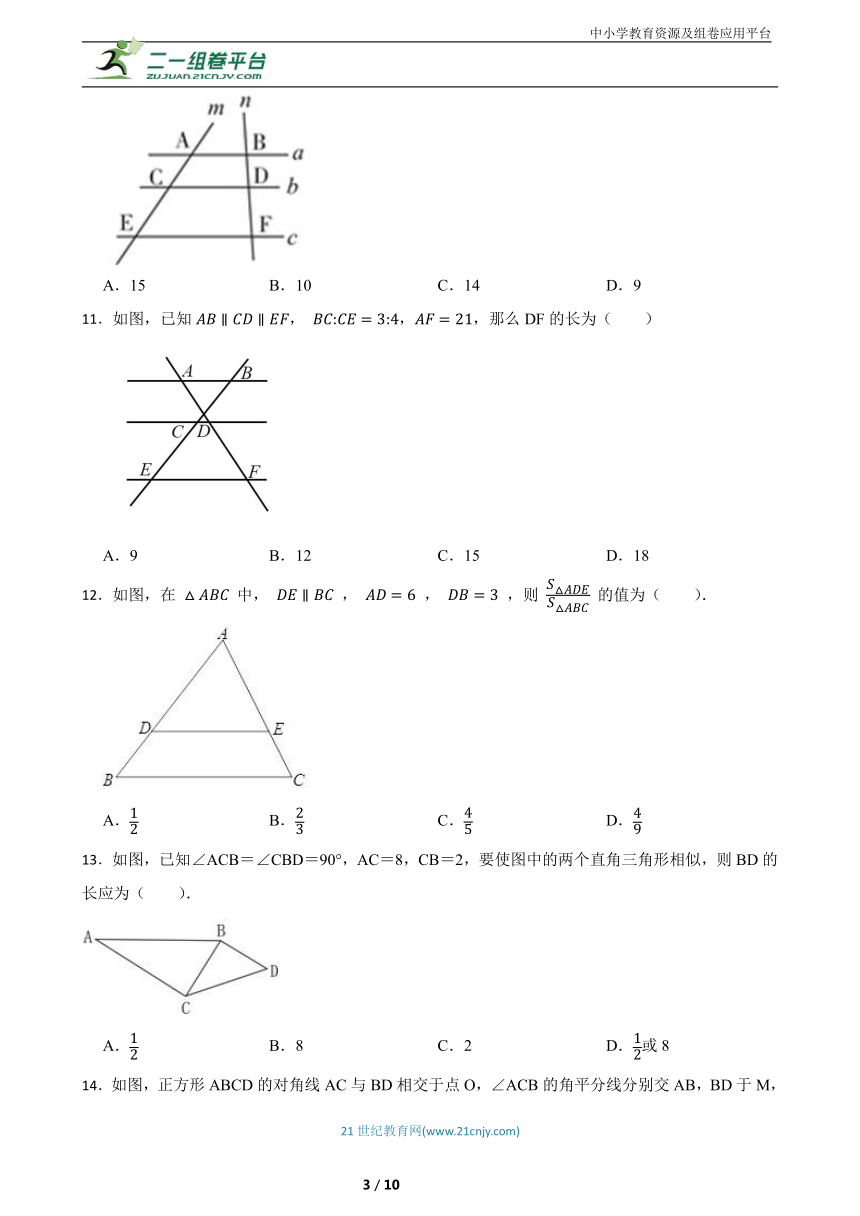

文档简介
中小学教育资源及组卷应用平台
6.4探索三角形相似的条件
一、填空题
1.已知△ABC与△DEF相似且面积比为9︰25,则△ABC与△DEF的相似比为 .
2.如图,在△ABC中,DE∥AB,且,则的值为
3.如图,已知它们分别交直线于点和点,如果,,那么线段的长是
4.如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP= .
5.若△ABC∽△A'B'C',∠A=40°,∠C=110°,则∠B'= .
6.如图,矩形的边在x轴上,,,把沿直线折叠,得到,交x轴于点E,则点D的坐标是.
二、单选题
7.如图,在平行四边形中,点E在边上,,连接交于点F,则的面积与的面积之比为( )
A. B. C. D.
8.如图所示,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的点、、都在横线上,如果线段的长为,那么的长是( )
A.2 B.3 C.6 D.8
9.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则 的值为( )
A. B. C. D.2
10.如图,已知直线 ,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若 , , ,则 的值是( )
A.15 B.10 C.14 D.9
11.如图,已知, ,,那么DF的长为( )
A.9 B.12 C.15 D.18
12.如图,在 中, , , ,则 的值为( ).
A. B. C. D.
13.如图,已知∠ACB=∠CBD=90°,AC=8,CB=2,要使图中的两个直角三角形相似,则BD的长应为( ).
A. B.8 C.2 D.或8
14.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
A. B. C.1 D.
15.如图,在 中, , ,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
16.中国古代数学家张爽证明勾股定理的弦图如图所示,它由四个全等的直角三角形和.一个小正方形EFGH组成,恰好拼成大正方形ABCD.作直线EG分别交AD,BC于点M, N.若图中两个正方形的面积分别是13和1,则MN的长为( )
A. B. C. D.
三、解答题
17.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长.
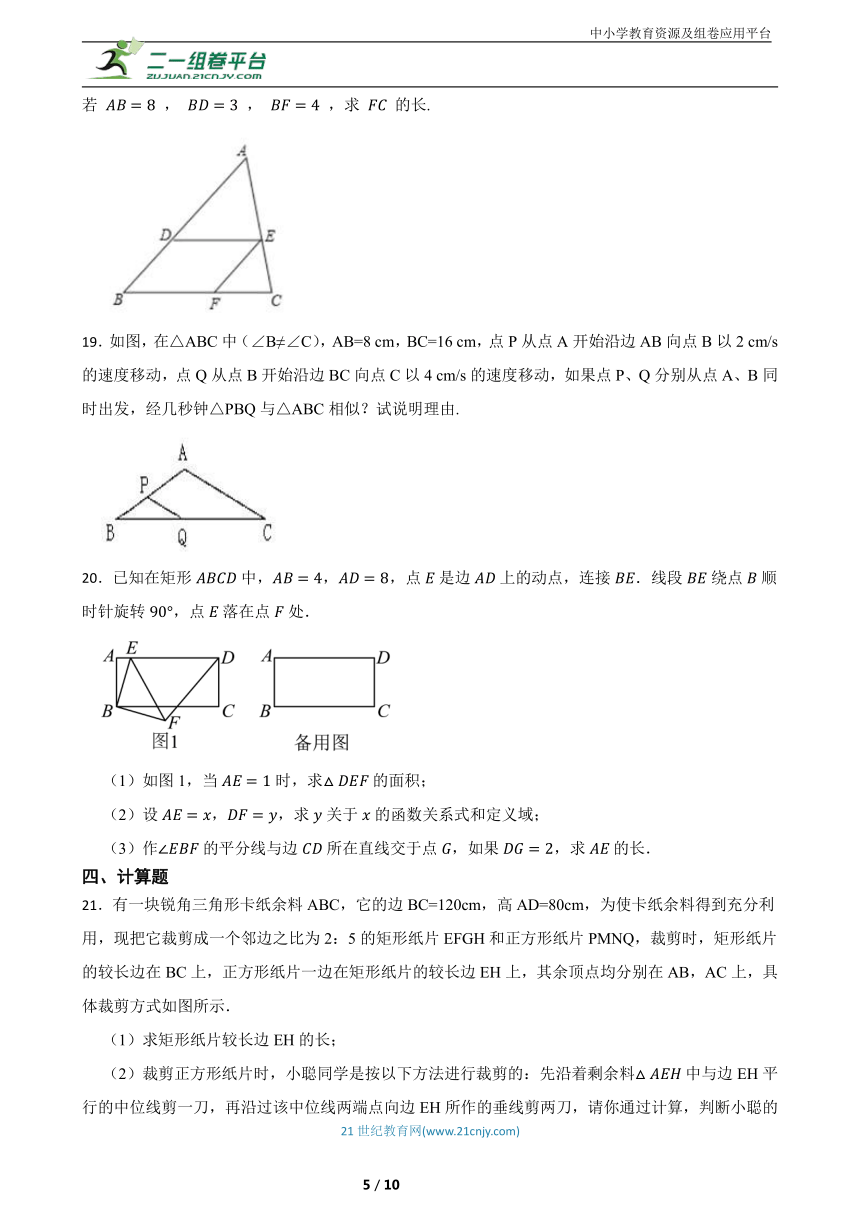
18.如图,在 中,点 , , 分别在 , , 上, , .若 , , ,求 的长.
19.如图,在△ABC中(∠B≠∠C),AB=8 cm,BC=16 cm,点P从点A开始沿边AB向点B以2 cm/s的速度移动,点Q从点B开始沿边BC向点C以4 cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
20.已知在矩形中,,,点是边上的动点,连接.线段绕点顺时针旋转,点落在点处.
(1)如图1,当时,求的面积;
(2)设,,求关于的函数关系式和定义域;
(3)作的平分线与边所在直线交于点,如果,求的长.
四、计算题
21.有一块锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点均分别在AB,AC上,具体裁剪方式如图所示.
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
22.阅读与思考,请阅读下列科普材料,并完成相应的任务.
图算法 图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系:得出,当时,.但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种利用特制的线条进行计算的方法就是图算法. 再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少? 我们可以利用公式求得的值,也可以设计一种图算法直接得出结果:我们先来画出一个的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值. 图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性.
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性:
①用公式计算:当,时,的值为多少;
②如图,在中,,是的角平分线,,,用你所学的几何知识求线段的长.
23.如图1,在锐角△ABC中,AB=5,AC=4,∠ACB=45°
(1)计算:求BC的长;
(2)操作:将图1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图2,当点C1在线段CA的延长线上时.
①求∠CC1A1的度数;
②求四边形A1BCC1的面积;
(3)探究:如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转所得到的△A1BC1中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
答案解析部分
1.【答案】3∶5
【知识点】相似三角形的性质
2.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】8
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】
【知识点】正方形的性质;相似三角形的判定与性质
5.【答案】30°
【知识点】相似三角形的性质
6.【答案】
【知识点】坐标与图形性质;勾股定理;矩形的性质;相似三角形的判定与性质
7.【答案】C
【知识点】平行四边形的性质;相似三角形的性质;相似三角形的判定
8.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
9.【答案】A
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
10.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
12.【答案】D
【知识点】相似三角形的性质
13.【答案】D
【知识点】相似三角形的判定
14.【答案】C
【知识点】角平分线的性质;正方形的性质;相似三角形的判定与性质
15.【答案】C
【知识点】相似三角形的判定
16.【答案】C
【知识点】三角形全等及其性质;勾股定理;相似三角形的判定与性质
17.【答案】(1);(2).
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】解:∵ ,
∴
∵ , ,
∴
解得
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
19.【答案】解:设经x秒钟△PBQ与△ABC相似,则AP=2xcm,BQ=4xcm,∵AB=8cm,BC=16cm,∴BP=AB﹣AP=(8﹣2x)cm,∵∠B是公共角,∵①当 ,即 时,△PBQ∽△ABC,解得:x=2;②当 ,即 时,△QBP∽△ABC,解得:x=0.8,∴经2或0.8秒钟△PBQ与△ABC相似.
【知识点】相似三角形的判定与性质
20.【答案】(1)
(2)()
(3)或
【知识点】函数解析式;矩形的判定与性质;相似三角形的判定与性质;旋转的性质
21.【答案】(1)75(2)小聪的剪法不正确
【知识点】相似三角形的判定与性质
22.【答案】(1)图算法方便;直观;或不用公式计算即可得出结果等;(2)①;②
【知识点】相似三角形的判定与性质
23.【答案】(1)BC=7(2)①∠CC1A=90°;②;(3)①最小值为﹣;最大值为:EP1=BC+BE=+7=.
【知识点】相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
1 / 10
6.4探索三角形相似的条件
一、填空题
1.已知△ABC与△DEF相似且面积比为9︰25,则△ABC与△DEF的相似比为 .
2.如图,在△ABC中,DE∥AB,且,则的值为
3.如图,已知它们分别交直线于点和点,如果,,那么线段的长是
4.如图,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP= .
5.若△ABC∽△A'B'C',∠A=40°,∠C=110°,则∠B'= .
6.如图,矩形的边在x轴上,,,把沿直线折叠,得到,交x轴于点E,则点D的坐标是.
二、单选题
7.如图,在平行四边形中,点E在边上,,连接交于点F,则的面积与的面积之比为( )
A. B. C. D.
8.如图所示,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的点、、都在横线上,如果线段的长为,那么的长是( )
A.2 B.3 C.6 D.8
9.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则 的值为( )
A. B. C. D.2
10.如图,已知直线 ,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若 , , ,则 的值是( )
A.15 B.10 C.14 D.9
11.如图,已知, ,,那么DF的长为( )
A.9 B.12 C.15 D.18
12.如图,在 中, , , ,则 的值为( ).
A. B. C. D.
13.如图,已知∠ACB=∠CBD=90°,AC=8,CB=2,要使图中的两个直角三角形相似,则BD的长应为( ).
A. B.8 C.2 D.或8
14.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
A. B. C.1 D.
15.如图,在 中, , ,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
16.中国古代数学家张爽证明勾股定理的弦图如图所示,它由四个全等的直角三角形和.一个小正方形EFGH组成,恰好拼成大正方形ABCD.作直线EG分别交AD,BC于点M, N.若图中两个正方形的面积分别是13和1,则MN的长为( )
A. B. C. D.
三、解答题
17.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长.
18.如图,在 中,点 , , 分别在 , , 上, , .若 , , ,求 的长.
19.如图,在△ABC中(∠B≠∠C),AB=8 cm,BC=16 cm,点P从点A开始沿边AB向点B以2 cm/s的速度移动,点Q从点B开始沿边BC向点C以4 cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
20.已知在矩形中,,,点是边上的动点,连接.线段绕点顺时针旋转,点落在点处.
(1)如图1,当时,求的面积;
(2)设,,求关于的函数关系式和定义域;
(3)作的平分线与边所在直线交于点,如果,求的长.
四、计算题
21.有一块锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点均分别在AB,AC上,具体裁剪方式如图所示.
(1)求矩形纸片较长边EH的长;
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
22.阅读与思考,请阅读下列科普材料,并完成相应的任务.
图算法 图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系:得出,当时,.但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种利用特制的线条进行计算的方法就是图算法. 再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少? 我们可以利用公式求得的值,也可以设计一种图算法直接得出结果:我们先来画出一个的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值. 图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性.
任务:
(1)请根据以上材料简要说明图算法的优越性;
(2)请用以下两种方法验证第二个例子中图算法的正确性:
①用公式计算:当,时,的值为多少;
②如图,在中,,是的角平分线,,,用你所学的几何知识求线段的长.
23.如图1,在锐角△ABC中,AB=5,AC=4,∠ACB=45°
(1)计算:求BC的长;
(2)操作:将图1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图2,当点C1在线段CA的延长线上时.
①求∠CC1A1的度数;
②求四边形A1BCC1的面积;
(3)探究:如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转所得到的△A1BC1中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.
答案解析部分
1.【答案】3∶5
【知识点】相似三角形的性质
2.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】8
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】
【知识点】正方形的性质;相似三角形的判定与性质
5.【答案】30°
【知识点】相似三角形的性质
6.【答案】
【知识点】坐标与图形性质;勾股定理;矩形的性质;相似三角形的判定与性质
7.【答案】C
【知识点】平行四边形的性质;相似三角形的性质;相似三角形的判定
8.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
9.【答案】A
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
10.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
12.【答案】D
【知识点】相似三角形的性质
13.【答案】D
【知识点】相似三角形的判定
14.【答案】C
【知识点】角平分线的性质;正方形的性质;相似三角形的判定与性质
15.【答案】C
【知识点】相似三角形的判定
16.【答案】C
【知识点】三角形全等及其性质;勾股定理;相似三角形的判定与性质
17.【答案】(1);(2).
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】解:∵ ,
∴
∵ , ,
∴
解得
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
19.【答案】解:设经x秒钟△PBQ与△ABC相似,则AP=2xcm,BQ=4xcm,∵AB=8cm,BC=16cm,∴BP=AB﹣AP=(8﹣2x)cm,∵∠B是公共角,∵①当 ,即 时,△PBQ∽△ABC,解得:x=2;②当 ,即 时,△QBP∽△ABC,解得:x=0.8,∴经2或0.8秒钟△PBQ与△ABC相似.
【知识点】相似三角形的判定与性质
20.【答案】(1)
(2)()
(3)或
【知识点】函数解析式;矩形的判定与性质;相似三角形的判定与性质;旋转的性质
21.【答案】(1)75(2)小聪的剪法不正确
【知识点】相似三角形的判定与性质
22.【答案】(1)图算法方便;直观;或不用公式计算即可得出结果等;(2)①;②
【知识点】相似三角形的判定与性质
23.【答案】(1)BC=7(2)①∠CC1A=90°;②;(3)①最小值为﹣;最大值为:EP1=BC+BE=+7=.
【知识点】相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
1 / 10
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
