2025届高考物理专题复习--机械振动(共31张ppt)
文档属性
| 名称 | 2025届高考物理专题复习--机械振动(共31张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 40.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-01 17:02:29 | ||
图片预览









文档简介
(共31张PPT)
机械振动
我们把物体或物体的一部分在一个位置附近的往复运动称为机械振动,简称振动。
特征:(1)有一个“中心位置”,也是振动物体静止时的位置;
(2)运动具有往复性。
机械振动
我们把小球和弹簧组成的系统称为弹簧振子,有时也简称为振子。
理想模型(1)小球看成质点;(2)不计阻力;(3)忽略弹簧的质量;
(4)弹簧始终在弹性限度内。
弹簧振子
弹簧振子
平衡位置:振子原来静止时的位置.
特点:合力为0,加速度为0,速度最大
弹簧最长(弹簧最短)
特点:合力最大 加速度最大 速度为0
某时刻的位移:从平衡位置指向振子在该时刻位置的有向线段。位移总是背离平衡位置。
振子在某段时间内的位移:由初位置指向末位置的有向线段。
五个对称:时间对称 空间对称 速度对称 力对称 能量对称
弹簧振子的平衡位置不一定在弹簧的原长位置,如:竖直方向弹簧阵子等
弹簧阵子的振动图像x-t图象
用横坐标表示物体运动的时间t,纵坐标表示振动物体运动过程中相对平衡位置的位移x,建立坐标系,如图.
t /s
x
横向
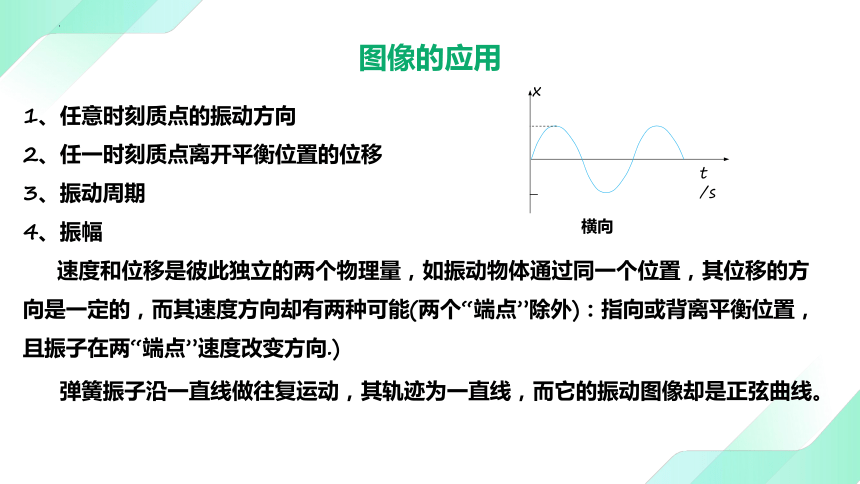
1、任意时刻质点的振动方向
2、任一时刻质点离开平衡位置的位移
3、振动周期
4、振幅
速度和位移是彼此独立的两个物理量,如振动物体通过同一个位置,其位移的方向是一定的,而其速度方向却有两种可能(两个“端点”除外):指向或背离平衡位置,且振子在两“端点”速度改变方向.)
弹簧振子沿一直线做往复运动,其轨迹为一直线,而它的振动图像却是正弦曲线。
t /s
x
横向
图像的应用
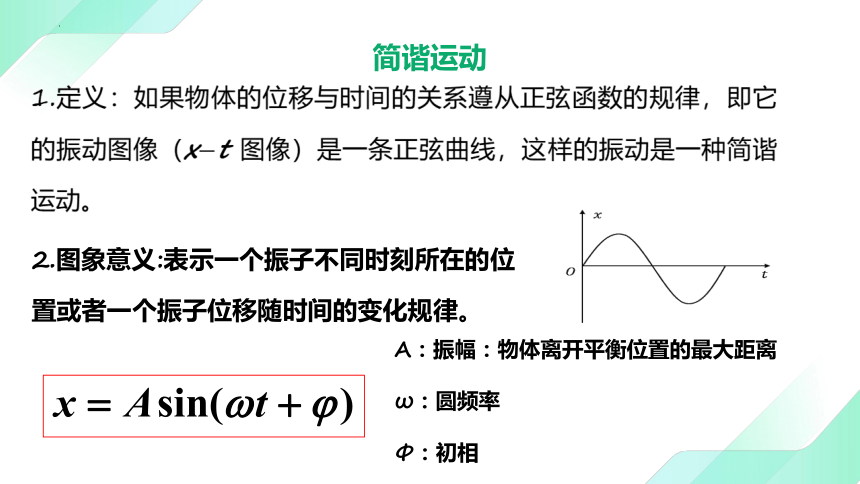
简谐运动
1.定义:如果物体的位移与时间的关系遵从正弦函数的规律,即它的振动图像(xt 图像)是一条正弦曲线,这样的振动是一种简谐运动。
2.图象意义:表示一个振子不同时刻所在的位置或者一个振子位移随时间的变化规律。
A:振幅:物体离开平衡位置的最大距离
ω:圆频率
Φ:初相
(1)任意时刻质点位移的大小和方向。如图甲所示,质点在t1、t2时刻的位移分别为x1和-x2。
3.图象应用:
(2)任意时刻质点的振动方向:看下一时刻质点的位置,如图乙中a点,下一时刻离平衡位置更远,故a点此刻向上振动。图乙中b点,下一时刻离平衡位置更近,故b此刻向上振动。
(3)斜率:该时刻速度的大小和方向.
简谐运动
简谐运动
4.简谐运动的对称性
如图所示,物体在A与B间运动,O点为平衡位置,C和D两点关于O点对称,则有:
(1)时间的对称:tOB=tBO=tOA=tAO,tOD=tDO=tOC=tCO,tDB=tBD=tAC=tCA
(2)速度的对称:
①物体连续两次经过同一点(如D点)的速度大小相等,方向相反;
②物体经过关于O点对称的两点(如C与D两点)的速度大小相等,方向可能相同,也可能相反.
简谐运动
(3)位移和加速度的对称
①物体经过同一点(如C点)时,位移和加速度均相同;
②物体经过关于O点对称的两点(如C点与D点)时,位移与加速度均大小相等,方向相反。
(4)动能、势能、机械能的对称
①物体连续两次经过同一点(如D点)时的动能、势能、机械能均相等;
②物体经过关于O点对称的两点(如C点与D点)时的动能、势能、机械能均相等。
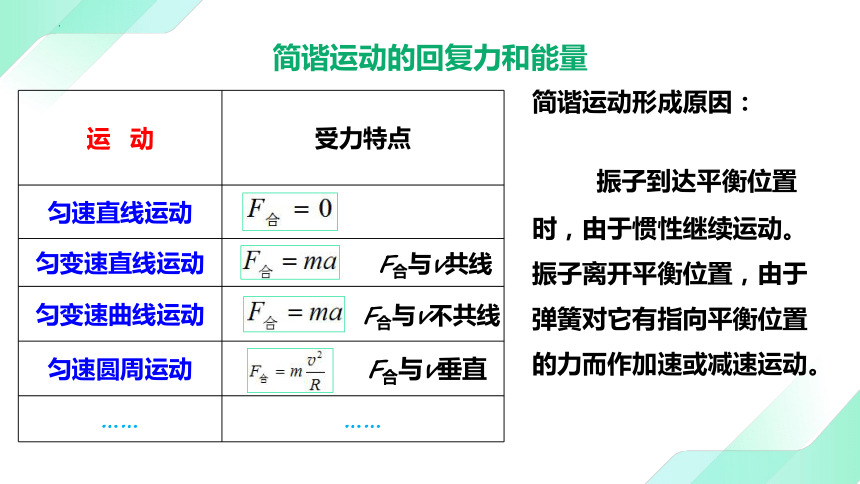
简谐运动的回复力和能量
运 动 受力特点
匀速直线运动
匀变速直线运动
匀变速曲线运动
匀速圆周运动
…… ……
F合与v共线
F合与v垂直
F合与v不共线
简谐运动形成原因:
振子到达平衡位置时,由于惯性继续运动。振子离开平衡位置,由于弹簧对它有指向平衡位置的力而作加速或减速运动。
回复力
1.定义:使振子回到平衡位置的力
回复力是按力的作用效果命名的
2.来源:可以是弹力,也可以是其它力;可以是某一个力,或几个力的合力,或某个力的分力.
3.大小: F=-kx
“-” 表示回复力方向始终与位移方向相反.
4.方向: 总是指向平衡位置.
5.简谐运动定义的另一种表述:如果质点所受的力与偏离平衡位置的位移大小成正比,并且总是指向平衡位置,其运动就是简谐运动。
即回复力满足 F= -kx的运动就是简谐运动。
注意:对一般的简谐运动,由于回复力不一定是弹簧的弹力,所以k不一定是劲度系数而是回复力与位移的比例系数。
例题:如图一劲度为k的轻弹簧上端固定,另一端挂一质量为m的小球,平衡时弹簧形变量为x0,下拉一段距离(没有超出弹性限度)后释放小球,小球的运动是简谐运动吗?其回复力是谁提供的?
x0
o
证明:平衡时
重力和弹力的合力提供回复力
x
kx0
k(x0+x)
kx
mg
mg
kx0
mg
当偏离平衡位置为x时
回复力:F=mg-k(x0+x)
得 F=-kx
小球运动是简谐运动
mg=kx0
mgsinθ
k(x0+x)
o
简谐运动的规律
动能
势能
0
增大
最大
减小
0
最大
减小
0
增大
最大
机械能
不变
O
Q
P
X
v
F、a
Q
Q-O
O
O-P
P
向左最大
向左减小
向右最大
向右最大
0
向右最大
向右增大
向右减小
0
0
向右增大
向右减小
向左增大
0
向左最大
简谐运动的规律
t
E
0
机械能
势能
动能
Q
P
O
做简谐运动时的Ek-t和Ep-t及E-t图象
在细线的一端拴上一个小球,另一端固定在悬点上,如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫作单摆。
单摆是实际摆的理想化模型
条件:
轻:绳重可忽略
细:阻力可忽略
软:绳力沿绳
长:摆角较小时才可看做简谐运动,绳长便于观察
无弹性:绳不可伸长
悬点要固定:不固定,摆长会发生变化。
单摆
单摆的回复力
l
m
O
θ
分析单摆的回复力
P
FT
G
F1
F
x
回复力F指向平衡位置O,与位移x反向。
故回复力可表示为:
F回=-kx
在θ很小时,
mg、l是定值
F =mgsin θ
令
单摆
B
A
O
P
G2
G1
沿切线指向平衡位置
(重力沿切线的分力提供回复力):
与该点速度方向垂直,只改变速度方向
F回=mgsinθ
回复力大小:
回复力方向:
作用:
向心力大小:
F向=T-mgcosθ
向心力方向:
沿半径指向悬点
作用:
单摆的周期
荷兰物理学家惠更斯(1629---1695)通过实验进一步得到:单摆做简谐运动的周期T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比,与振幅、摆球质量无关.
单摆周期公式:
T=2π
惠更斯(荷兰)
理解:(1)单摆周期与摆长和重力加速度有关,与振幅和质量无关。
(2)摆长、重力加速度都一定时,周期和频率也一定,
通常称为单摆的固有周期和固有频率。
(3)注意事项:
摆长L:悬点到球心的距离
适用条件:单摆做简谐运动θ<50
利用 单摆测重力加速度
等效摆
单摆的周期
固有周期
像弹簧振子和单摆这样的振动系统在没有外力干预的情况下做简谐运动,周期或频率与振幅无关,仅有系统自身的性质决定,我们把这种振动称为固有振动,其振动频率称为固有频率。
振幅随时间逐渐减小
振动系统的能量越来越少
1、固有频率:简谐运动的物体受到的回复力是振动系统内部的相互作用力.如果振动系统不受外力的作用,此时系统的振动叫做固有振动,其振动频率称为固有振动.
2、阻尼振动:振动系统受到的阻力作用叫做阻尼.阻尼振动的振幅不断减小.振动系统受到的阻尼越大,振幅减小得越快.当阻尼很小时,就可以忽略,当成简谐运动来处理.
例:空气中的弹簧振子和单摆,由于受到空气阻力的作用,做振幅逐渐减小的运动叫做阻尼振动.而钟摆能保持振幅不变,原因是定时补充能量的结果.
受迫振动 共振
阻尼振动
1、阻尼振动:振动系统在阻尼(摩擦或其他阻力)作用下的振幅逐渐减小的振动.
2、阻尼振动的图像
3、振动系统受到的阻尼越大,振幅减小得越快,阻尼过大时,系统将不能发生振动。
4、实际的振动一定是阻尼振动
振动系统能量衰减的两种方式:
1.一种是由于振动系统受到摩擦或其他阻力的作用,使振动系统的机械能逐渐转化为内能。
2.另一种是由于振动系统引起邻近介质中各质点的振动,使能量向四周辐射出去,从而自身机械能减少。
生活中的实际的振动一定有阻力,
故一定是阻尼振动
思考:阻尼振动中,由于存在阻力,振幅不断减小,故振动系统的机械能将不断减少,那么,振动系统的周期和频率也会发生变化吗?
T
T
T
振动周期与振幅无关,故阻尼振动中周期和频率不变!
单摆:
简谐运动 阻尼振动
产生条件 理想模型,不受阻力
受到阻力作用
振幅 不变 减小
频率 由系统本身决定 频率不变
振动图像
简谐运动与阻尼振动的比较
阻尼振动最终要停下来,那么怎样才能产生持续的振动呢?
用周期性的外力作用于振动系统,补偿系统机械能的损耗,使系统持续地振动下去。
1.驱动力:
周期性作用于振动系统的外力叫做驱动力。
2.受迫振动:
系统在驱动力作用下的振动,叫做受迫振动。
受迫振动稳定时的频率等于驱动力的频率,跟系统的固有频率无关。
受迫振动
当系统做受迫振动时,驱动力的频率与物体的固有频率相差越小,受迫振动的振幅越大;当驱动力的频率与物体的固有频率相等时,受迫振动的振幅最大。
共振
1.定义:驱动力的频率f 等于物体的固有频率f0时,受迫振动的振幅最大,这种现象叫做共振。
横轴:表示驱动力的频率
纵轴:表示受迫振动的振幅
2.共振曲线:
3.受迫振动的规律
f驱 = f固 时,振幅有最大值;
f驱 与 f固 差别越大时,振幅越小。
共振
汇报人:WPS
机械振动
我们把物体或物体的一部分在一个位置附近的往复运动称为机械振动,简称振动。
特征:(1)有一个“中心位置”,也是振动物体静止时的位置;
(2)运动具有往复性。
机械振动
我们把小球和弹簧组成的系统称为弹簧振子,有时也简称为振子。
理想模型(1)小球看成质点;(2)不计阻力;(3)忽略弹簧的质量;
(4)弹簧始终在弹性限度内。
弹簧振子
弹簧振子
平衡位置:振子原来静止时的位置.
特点:合力为0,加速度为0,速度最大
弹簧最长(弹簧最短)
特点:合力最大 加速度最大 速度为0
某时刻的位移:从平衡位置指向振子在该时刻位置的有向线段。位移总是背离平衡位置。
振子在某段时间内的位移:由初位置指向末位置的有向线段。
五个对称:时间对称 空间对称 速度对称 力对称 能量对称
弹簧振子的平衡位置不一定在弹簧的原长位置,如:竖直方向弹簧阵子等
弹簧阵子的振动图像x-t图象
用横坐标表示物体运动的时间t,纵坐标表示振动物体运动过程中相对平衡位置的位移x,建立坐标系,如图.
t /s
x
横向
1、任意时刻质点的振动方向
2、任一时刻质点离开平衡位置的位移
3、振动周期
4、振幅
速度和位移是彼此独立的两个物理量,如振动物体通过同一个位置,其位移的方向是一定的,而其速度方向却有两种可能(两个“端点”除外):指向或背离平衡位置,且振子在两“端点”速度改变方向.)
弹簧振子沿一直线做往复运动,其轨迹为一直线,而它的振动图像却是正弦曲线。
t /s
x
横向
图像的应用
简谐运动
1.定义:如果物体的位移与时间的关系遵从正弦函数的规律,即它的振动图像(xt 图像)是一条正弦曲线,这样的振动是一种简谐运动。
2.图象意义:表示一个振子不同时刻所在的位置或者一个振子位移随时间的变化规律。
A:振幅:物体离开平衡位置的最大距离
ω:圆频率
Φ:初相
(1)任意时刻质点位移的大小和方向。如图甲所示,质点在t1、t2时刻的位移分别为x1和-x2。
3.图象应用:
(2)任意时刻质点的振动方向:看下一时刻质点的位置,如图乙中a点,下一时刻离平衡位置更远,故a点此刻向上振动。图乙中b点,下一时刻离平衡位置更近,故b此刻向上振动。
(3)斜率:该时刻速度的大小和方向.
简谐运动
简谐运动
4.简谐运动的对称性
如图所示,物体在A与B间运动,O点为平衡位置,C和D两点关于O点对称,则有:
(1)时间的对称:tOB=tBO=tOA=tAO,tOD=tDO=tOC=tCO,tDB=tBD=tAC=tCA
(2)速度的对称:
①物体连续两次经过同一点(如D点)的速度大小相等,方向相反;
②物体经过关于O点对称的两点(如C与D两点)的速度大小相等,方向可能相同,也可能相反.
简谐运动
(3)位移和加速度的对称
①物体经过同一点(如C点)时,位移和加速度均相同;
②物体经过关于O点对称的两点(如C点与D点)时,位移与加速度均大小相等,方向相反。
(4)动能、势能、机械能的对称
①物体连续两次经过同一点(如D点)时的动能、势能、机械能均相等;
②物体经过关于O点对称的两点(如C点与D点)时的动能、势能、机械能均相等。
简谐运动的回复力和能量
运 动 受力特点
匀速直线运动
匀变速直线运动
匀变速曲线运动
匀速圆周运动
…… ……
F合与v共线
F合与v垂直
F合与v不共线
简谐运动形成原因:
振子到达平衡位置时,由于惯性继续运动。振子离开平衡位置,由于弹簧对它有指向平衡位置的力而作加速或减速运动。
回复力
1.定义:使振子回到平衡位置的力
回复力是按力的作用效果命名的
2.来源:可以是弹力,也可以是其它力;可以是某一个力,或几个力的合力,或某个力的分力.
3.大小: F=-kx
“-” 表示回复力方向始终与位移方向相反.
4.方向: 总是指向平衡位置.
5.简谐运动定义的另一种表述:如果质点所受的力与偏离平衡位置的位移大小成正比,并且总是指向平衡位置,其运动就是简谐运动。
即回复力满足 F= -kx的运动就是简谐运动。
注意:对一般的简谐运动,由于回复力不一定是弹簧的弹力,所以k不一定是劲度系数而是回复力与位移的比例系数。
例题:如图一劲度为k的轻弹簧上端固定,另一端挂一质量为m的小球,平衡时弹簧形变量为x0,下拉一段距离(没有超出弹性限度)后释放小球,小球的运动是简谐运动吗?其回复力是谁提供的?
x0
o
证明:平衡时
重力和弹力的合力提供回复力
x
kx0
k(x0+x)
kx
mg
mg
kx0
mg
当偏离平衡位置为x时
回复力:F=mg-k(x0+x)
得 F=-kx
小球运动是简谐运动
mg=kx0
mgsinθ
k(x0+x)
o
简谐运动的规律
动能
势能
0
增大
最大
减小
0
最大
减小
0
增大
最大
机械能
不变
O
Q
P
X
v
F、a
Q
Q-O
O
O-P
P
向左最大
向左减小
向右最大
向右最大
0
向右最大
向右增大
向右减小
0
0
向右增大
向右减小
向左增大
0
向左最大
简谐运动的规律
t
E
0
机械能
势能
动能
Q
P
O
做简谐运动时的Ek-t和Ep-t及E-t图象
在细线的一端拴上一个小球,另一端固定在悬点上,如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫作单摆。
单摆是实际摆的理想化模型
条件:
轻:绳重可忽略
细:阻力可忽略
软:绳力沿绳
长:摆角较小时才可看做简谐运动,绳长便于观察
无弹性:绳不可伸长
悬点要固定:不固定,摆长会发生变化。
单摆
单摆的回复力
l
m
O
θ
分析单摆的回复力
P
FT
G
F1
F
x
回复力F指向平衡位置O,与位移x反向。
故回复力可表示为:
F回=-kx
在θ很小时,
mg、l是定值
F =mgsin θ
令
单摆
B
A
O
P
G2
G1
沿切线指向平衡位置
(重力沿切线的分力提供回复力):
与该点速度方向垂直,只改变速度方向
F回=mgsinθ
回复力大小:
回复力方向:
作用:
向心力大小:
F向=T-mgcosθ
向心力方向:
沿半径指向悬点
作用:
单摆的周期
荷兰物理学家惠更斯(1629---1695)通过实验进一步得到:单摆做简谐运动的周期T与摆长l的二次方根成正比,与重力加速度g的二次方根成反比,与振幅、摆球质量无关.
单摆周期公式:
T=2π
惠更斯(荷兰)
理解:(1)单摆周期与摆长和重力加速度有关,与振幅和质量无关。
(2)摆长、重力加速度都一定时,周期和频率也一定,
通常称为单摆的固有周期和固有频率。
(3)注意事项:
摆长L:悬点到球心的距离
适用条件:单摆做简谐运动θ<50
利用 单摆测重力加速度
等效摆
单摆的周期
固有周期
像弹簧振子和单摆这样的振动系统在没有外力干预的情况下做简谐运动,周期或频率与振幅无关,仅有系统自身的性质决定,我们把这种振动称为固有振动,其振动频率称为固有频率。
振幅随时间逐渐减小
振动系统的能量越来越少
1、固有频率:简谐运动的物体受到的回复力是振动系统内部的相互作用力.如果振动系统不受外力的作用,此时系统的振动叫做固有振动,其振动频率称为固有振动.
2、阻尼振动:振动系统受到的阻力作用叫做阻尼.阻尼振动的振幅不断减小.振动系统受到的阻尼越大,振幅减小得越快.当阻尼很小时,就可以忽略,当成简谐运动来处理.
例:空气中的弹簧振子和单摆,由于受到空气阻力的作用,做振幅逐渐减小的运动叫做阻尼振动.而钟摆能保持振幅不变,原因是定时补充能量的结果.
受迫振动 共振
阻尼振动
1、阻尼振动:振动系统在阻尼(摩擦或其他阻力)作用下的振幅逐渐减小的振动.
2、阻尼振动的图像
3、振动系统受到的阻尼越大,振幅减小得越快,阻尼过大时,系统将不能发生振动。
4、实际的振动一定是阻尼振动
振动系统能量衰减的两种方式:
1.一种是由于振动系统受到摩擦或其他阻力的作用,使振动系统的机械能逐渐转化为内能。
2.另一种是由于振动系统引起邻近介质中各质点的振动,使能量向四周辐射出去,从而自身机械能减少。
生活中的实际的振动一定有阻力,
故一定是阻尼振动
思考:阻尼振动中,由于存在阻力,振幅不断减小,故振动系统的机械能将不断减少,那么,振动系统的周期和频率也会发生变化吗?
T
T
T
振动周期与振幅无关,故阻尼振动中周期和频率不变!
单摆:
简谐运动 阻尼振动
产生条件 理想模型,不受阻力
受到阻力作用
振幅 不变 减小
频率 由系统本身决定 频率不变
振动图像
简谐运动与阻尼振动的比较
阻尼振动最终要停下来,那么怎样才能产生持续的振动呢?
用周期性的外力作用于振动系统,补偿系统机械能的损耗,使系统持续地振动下去。
1.驱动力:
周期性作用于振动系统的外力叫做驱动力。
2.受迫振动:
系统在驱动力作用下的振动,叫做受迫振动。
受迫振动稳定时的频率等于驱动力的频率,跟系统的固有频率无关。
受迫振动
当系统做受迫振动时,驱动力的频率与物体的固有频率相差越小,受迫振动的振幅越大;当驱动力的频率与物体的固有频率相等时,受迫振动的振幅最大。
共振
1.定义:驱动力的频率f 等于物体的固有频率f0时,受迫振动的振幅最大,这种现象叫做共振。
横轴:表示驱动力的频率
纵轴:表示受迫振动的振幅
2.共振曲线:
3.受迫振动的规律
f驱 = f固 时,振幅有最大值;
f驱 与 f固 差别越大时,振幅越小。
共振
汇报人:WPS
同课章节目录
