2025届高考物理专题复习--匀变速直线运动的规律(共35张ppt)
文档属性
| 名称 | 2025届高考物理专题复习--匀变速直线运动的规律(共35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-02 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
第一章 运动的描述
匀变速直线运动的规律
目录
contents
匀变速直线运动的平均速度公式
01
02
匀变速直线运动的位移差公式
03
初速度为零的匀加速直线运动的比例式
04
典例分析
回顾知识
3个公式中都含有 a,能不能推出不含a却含有v0、 v、 x、t的公式呢?
无位移
无末速度
无时间
5个:v0、 v、 a、x、t。
任何一个匀变速直线运动过程涉及物理量:
4类:速度、加速度、位移、时间;
速度与时间关系:
位移与时间关系:
速度与位移关系:
匀变速直线运动
加速度恒定不变的变速直线运动
匀变速直线运动的平均速度公式
01
(重要推论)
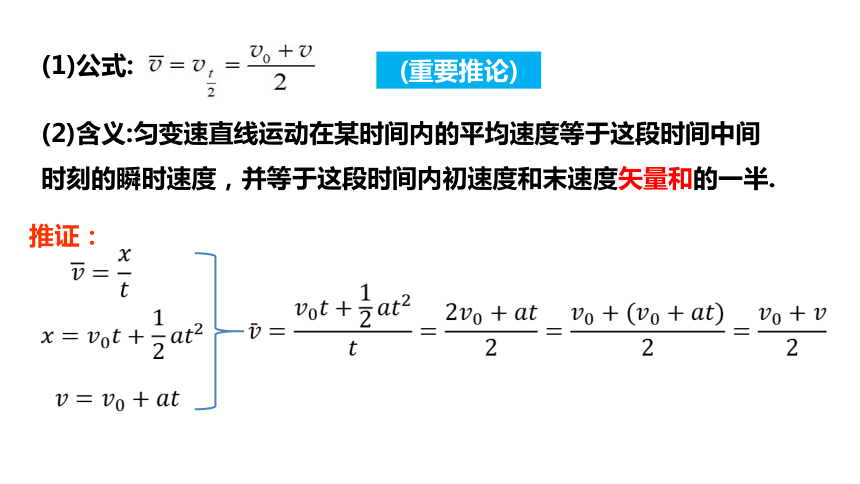
(1)公式:
(2)含义:匀变速直线运动在某时间内的平均速度等于这段时间中间时刻的瞬时速度,并等于这段时间内初速度和末速度矢量和的一半.
推证:
t 时间内的平均速度等于t/2时刻的瞬时速度
又因为
注意:此公式只适用于匀变速直线运动
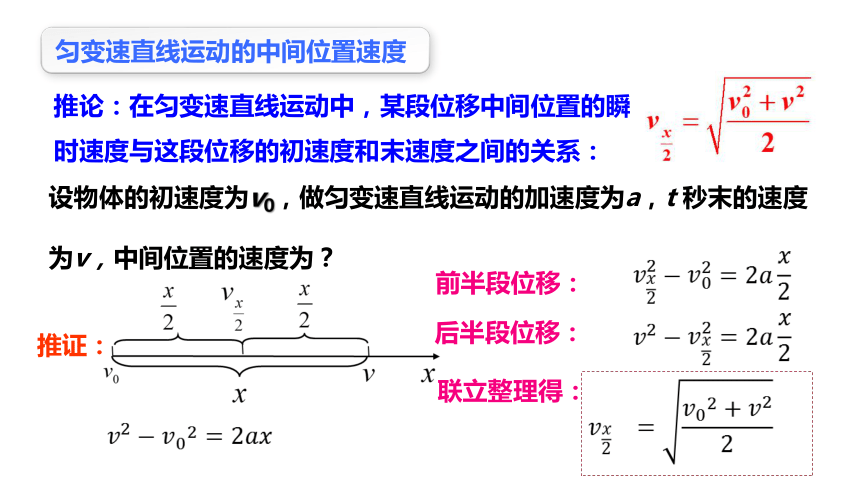
匀变速直线运动的中间位置速度
推论:在匀变速直线运动中,某段位移中间位置的瞬时速度与这段位移的初速度和末速度之间的关系:
设物体的初速度为v0,做匀变速直线运动的加速度为a,t 秒末的速度为v,中间位置的速度为?
联立整理得:
前半段位移:
后半段位移:
推证:
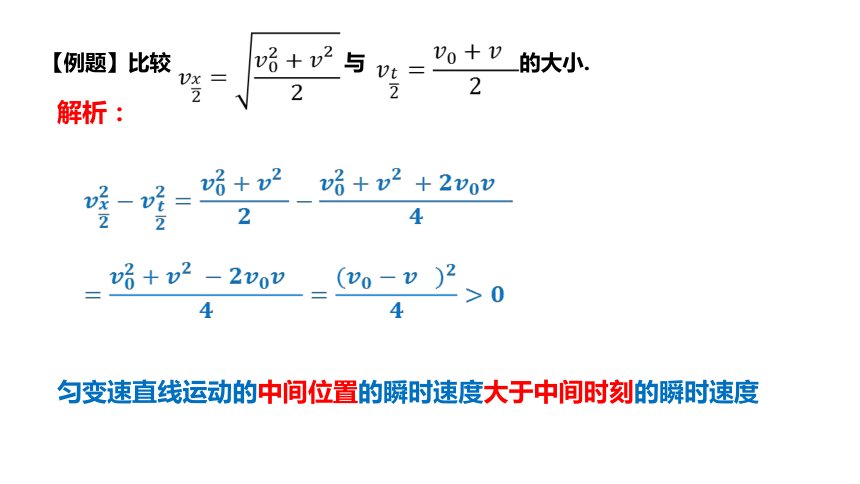
解析:
【例题】比较 与 的大小.
匀变速直线运动的中间位置的瞬时速度大于中间时刻的瞬时速度
匀变速直线运动的位移差公式
02
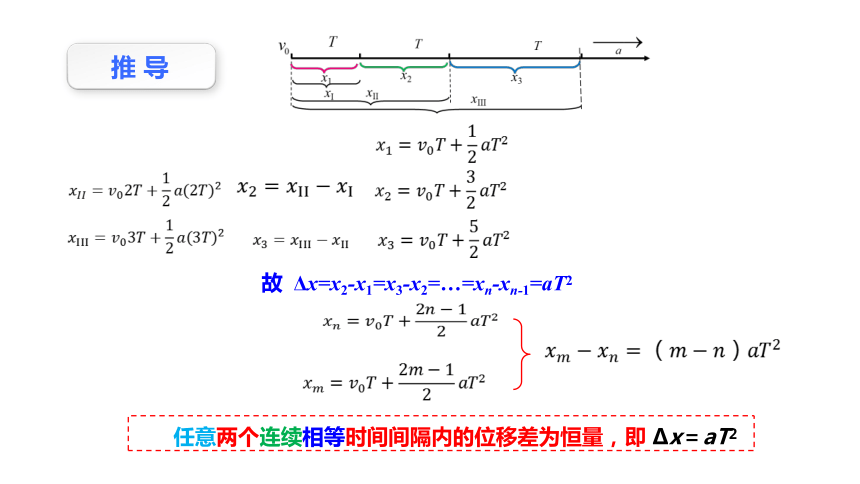
(1)含义:做匀变速直线运动的物体在任意两个连续相等的时间T内,位移之差为一恒量,即:
(2)表达式:
重要推论:逐差相等
推广: △xmn=xm-xn=(m-n)aT2
Δx=x2-x1=x3-x2=…=xn-xn-1=aT2 (恒量)
任意两个连续相等时间间隔内的位移差为恒量,即 x=aT2
推 导
故 Δx=x2-x1=x3-x2=…=xn-xn-1=aT2
初速度为零的匀加速直线运动的比例式
03
建立时间坐标轴,把初速度为零的匀变速直线运动按时间T等分,如下图所示:
初速度为零的匀加速直线运动的速度公式:
可得:
已知:
所以:
①1T 秒末,2T秒末,…….瞬时速度之比:
建立时间坐标轴,把初速度为零的匀变速直线运动按时间T等分,如下图所示:
初速度为零的匀加速直线运动的位移公式:
可得:
已知:
所以:
②1T 内,2T 内,3T 内,…的位移之比
建立时间坐标轴,把初速度为零的匀变速直线运动按时间T等分,如下图
所示:
由图可得:
已知:
可得:
③第一个T内,第二个T内,第三个T内…的位移比
建立位移坐标轴,把初速度为零的匀变速直线运动按位移s等分,如下图
所示:
初速度为零的匀加速直线运动的时间公式:
可得:
所以:
④前1个s,前2个s,前3个s,…所用时间的比值:
建立位移坐标轴,把初速度为零的匀变速直线运动按位移s等分,如下图
所示:
初速度为零的匀加速直线运动的位移速度关系式:
可得:
所以:
⑤第1个s末,第2个s末,第3个s末…的速度之比:
建立位移坐标轴,把初速度为零的匀变速直线运动按位移s等分,如下图
所示:
由图可得:
已知:
所以:
⑥通过第1个s,通过第2个s,通过第3个s…所用时间的比值:
1.初速度为0的匀加速直线运动,按时间等分(设相等的时间间隔为T),则:
(1)T末、2T末、3T末、…、nT末的瞬时速度之比为:
v1∶v2∶v3∶…∶vn=1∶2∶3∶…∶n.
(2)T内、2T内、3T内、…、nT内的位移之比为:
x1∶x2∶x3∶…∶xn=12∶22∶32∶…∶n2.
(3)第一个T内、第二个T内、第三个T内、…、第n个T内的位移之比为:
x1′∶x2′∶x3′∶…∶xn′=1∶3∶5∶…∶(2n-1).
结论汇总
2.初速度为0的匀加速直线运动,按位移等分(设相等的位移为x),则:
(1)通过前x、前2x、前3x、…、前nx的位移时的瞬时速度之比为:
(2)通过前x、前2x、前3x、…、前nx的位移所用时间之比为:
(3)通过连续相同的位移所用时间之比为:
【特别提醒】
(1)以上比例成立的前提是物体做初速度为零的匀加速直线运动。
(2)对于末速度为零的匀减速直线运动,可把它看成逆向的初速度为零的匀加速直线运动,应用比例关系,可使问题简化。
1.思考判断
(1)匀变速直线运动是加速度均匀变化的直线运动。( )
(2)匀变速直线运动的位移是均匀增加的。( )
(3)匀变速直线运动是加速度不变而速度均匀变化的直线运动。( )
(4)在匀变速直线运动中,中间时刻的速度一定小于该段时间内位移中点的速度。( )
×
×
√
√
2.(2023·重庆一诊)2022年北京冬奥会单板滑雪项目中的助滑道可简化为如图1所示的斜面模型。设一运动员从助滑道的顶端A点由静止开始匀加速下滑,最初2 s内的位移为10 m,则他滑到离顶端25 m的B点时的速度大约为( )
A.10 m/s B.13 m/s
C.16 m/s D.19 m/s
C
例3 如图4所示,一辆汽车在平直公路上做匀加速直线运动,从树A开始,在相等的时间内依次经过B、C、D、E 四棵树,已知树A、B 间距为s1,树D、E 间距为s2,则树B、D 间距为( )
解决匀变速直线运动的常用推论
角度
A
平均速度公式的应用
A.s1+s2 B.2s1+s2 C.s1+2s2 D.2(s1+s2)
角度
D
位移差公式的应用
例5 (2023·山东日照市高三月考)小金开车在石村村口A处停了一会,接着由静止开始匀加速直线行驶,途经B、C、D、E四个石墩,如图6所示。已知B到C、C到D、D到E的时间相等,B、C间距离为4 m,C、D间距离为6 m,根据以上信息,以下说法正确的是( )
图6
A.可以求出汽车通过C点时的速度大小
B.可以求出汽车的加速度大小
C.可以求得汽车在A、B之间的行驶时间
D.可以求得A、E之间的距离
例2 (多选)(2023·河北石家庄模拟)如图3所示,某飞机着陆时的速度v0=216 km/h,随后沿直线匀减速滑行到静止。从飞机着陆开始计时,该飞机在倒数第4 s内的位移为7 m,下列说法正确的是( )
图3
AC
A.该飞机的加速度大小为2 m/s2
B.该飞机着陆后5 s时的速度大小为40 m/s
C.该飞机在跑道上滑行的时间为30 s
D.该飞机在跑道上滑行的距离为1 800 m
跟踪训练
C
1.某质点做直线运动,位置随时间变化的关系式为x=100t-10t2+100 m,则对这个质点的运动描述正确的是( )
A.初速度为0
B.加速度为20 m/s2
C.在3 s末,瞬时速度为40 m/s
D.做匀加速直线运动
例1 (2022·江苏盐城模拟)近两年,交警将“礼让行人”作为管理重点,“斑马线前车让人”现已逐渐成为一种普遍现象,如图2所示。司机小明驾车以12 m/s的速度,在平直的城市道路上沿直线行驶。看到斑马线有行人后立即以大小为2 m/s2的加速度刹车,车停住时车头刚好碰到斑马线。等待行人10 s后(人已走过),又用了8 s时间匀加速至原来的速度。开始刹车时设为计时起点(即t=0),求:
图2
(1)车第3 s末的瞬时速度大小;
(2)车前10 s内的位移大小;
(3)从开始刹车到恢复至原来速度这段时间内,车的平均速度大小。
刹车陷阱
B
例4 (2023·广东珠海模拟)如图5为港珠澳大桥上四段110 m的等跨钢箱连续梁桥,若汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,则( )
角度
A.通过cd段的时间为t
B.通过ce段的时间为(2-)t
C.ae段的平均速度等于c点的瞬时速度
D.ac段的平均速度等于b点的瞬时速度
对点练2 匀变速直线运动的推论及应用
ABD
5.(多选)一质点做匀加速直线运动,第3 s内的位移是2 m,第4 s内的位移是2.5 m,那么以下说法中正确的是( )
A.这2 s内的平均速度是2.25 m/s
B.第3 s末的瞬时速度是2.25 m/s
C.质点的加速度是0.125 m/s2
D.质点的加速度是0.5 m/s2
跟踪训练
2.(2023·山东日照质检)一物体做匀加速直线运动,通过一段位移Δs所用时间为2t,紧接着通过下一段位移Δs所用时间为t。则物体运动的加速度大小为( )
C
3.如图7甲为游客排队滑冰滑梯的场景,在工作人员的引导下,每间隔相同时间从滑梯顶端由静止开始滑下一名游客,将某次拍到的滑梯上同时有多名游客的照片简化为如图乙所示,已知A、B和B、C间的距离分别为2.5 m和3.5 m,若游客在滑梯上做匀加速直线运动,求:
图7
(1)C、D间的距离;
(2)此刻A的上端滑道上还有几个人;
(3)此时A距滑道顶端的距离。
2.某短跑运动员完成100 m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中,该运动员用12 s跑完全程,已知该运动员在加速阶段的位移和匀速阶段的位移之比为1∶4,则该运动员在加速阶段的加速度为( )
A.2.0 m/s2 B.2.5 m/s2 C.3.0 m/s2 D.3.5 m/s2
B
3.高速公路的ETC电子收费系统如图1所示,ETC通道的长度是识别区起点到自动栏杆的水平距离。某汽车以5 m/s的速度匀速进入识别区,ETC天线用了0.3 s的时间识别车载电子标签,识别完成后发出“滴”的一声,司机发现自动栏杆没有抬起,于是采取制动刹车,汽车刚好没有撞杆。已知司机的反应时间为0.5 s,刹车的加速度大小为2.5 m/s2,则该ETC通道的长度约为( )
B
A.7 m B.9 m
C.11 m D.13 m
B
第一章 运动的描述
匀变速直线运动的规律
目录
contents
匀变速直线运动的平均速度公式
01
02
匀变速直线运动的位移差公式
03
初速度为零的匀加速直线运动的比例式
04
典例分析
回顾知识
3个公式中都含有 a,能不能推出不含a却含有v0、 v、 x、t的公式呢?
无位移
无末速度
无时间
5个:v0、 v、 a、x、t。
任何一个匀变速直线运动过程涉及物理量:
4类:速度、加速度、位移、时间;
速度与时间关系:
位移与时间关系:
速度与位移关系:
匀变速直线运动
加速度恒定不变的变速直线运动
匀变速直线运动的平均速度公式
01
(重要推论)
(1)公式:
(2)含义:匀变速直线运动在某时间内的平均速度等于这段时间中间时刻的瞬时速度,并等于这段时间内初速度和末速度矢量和的一半.
推证:
t 时间内的平均速度等于t/2时刻的瞬时速度
又因为
注意:此公式只适用于匀变速直线运动
匀变速直线运动的中间位置速度
推论:在匀变速直线运动中,某段位移中间位置的瞬时速度与这段位移的初速度和末速度之间的关系:
设物体的初速度为v0,做匀变速直线运动的加速度为a,t 秒末的速度为v,中间位置的速度为?
联立整理得:
前半段位移:
后半段位移:
推证:
解析:
【例题】比较 与 的大小.
匀变速直线运动的中间位置的瞬时速度大于中间时刻的瞬时速度
匀变速直线运动的位移差公式
02
(1)含义:做匀变速直线运动的物体在任意两个连续相等的时间T内,位移之差为一恒量,即:
(2)表达式:
重要推论:逐差相等
推广: △xmn=xm-xn=(m-n)aT2
Δx=x2-x1=x3-x2=…=xn-xn-1=aT2 (恒量)
任意两个连续相等时间间隔内的位移差为恒量,即 x=aT2
推 导
故 Δx=x2-x1=x3-x2=…=xn-xn-1=aT2
初速度为零的匀加速直线运动的比例式
03
建立时间坐标轴,把初速度为零的匀变速直线运动按时间T等分,如下图所示:
初速度为零的匀加速直线运动的速度公式:
可得:
已知:
所以:
①1T 秒末,2T秒末,…….瞬时速度之比:
建立时间坐标轴,把初速度为零的匀变速直线运动按时间T等分,如下图所示:
初速度为零的匀加速直线运动的位移公式:
可得:
已知:
所以:
②1T 内,2T 内,3T 内,…的位移之比
建立时间坐标轴,把初速度为零的匀变速直线运动按时间T等分,如下图
所示:
由图可得:
已知:
可得:
③第一个T内,第二个T内,第三个T内…的位移比
建立位移坐标轴,把初速度为零的匀变速直线运动按位移s等分,如下图
所示:
初速度为零的匀加速直线运动的时间公式:
可得:
所以:
④前1个s,前2个s,前3个s,…所用时间的比值:
建立位移坐标轴,把初速度为零的匀变速直线运动按位移s等分,如下图
所示:
初速度为零的匀加速直线运动的位移速度关系式:
可得:
所以:
⑤第1个s末,第2个s末,第3个s末…的速度之比:
建立位移坐标轴,把初速度为零的匀变速直线运动按位移s等分,如下图
所示:
由图可得:
已知:
所以:
⑥通过第1个s,通过第2个s,通过第3个s…所用时间的比值:
1.初速度为0的匀加速直线运动,按时间等分(设相等的时间间隔为T),则:
(1)T末、2T末、3T末、…、nT末的瞬时速度之比为:
v1∶v2∶v3∶…∶vn=1∶2∶3∶…∶n.
(2)T内、2T内、3T内、…、nT内的位移之比为:
x1∶x2∶x3∶…∶xn=12∶22∶32∶…∶n2.
(3)第一个T内、第二个T内、第三个T内、…、第n个T内的位移之比为:
x1′∶x2′∶x3′∶…∶xn′=1∶3∶5∶…∶(2n-1).
结论汇总
2.初速度为0的匀加速直线运动,按位移等分(设相等的位移为x),则:
(1)通过前x、前2x、前3x、…、前nx的位移时的瞬时速度之比为:
(2)通过前x、前2x、前3x、…、前nx的位移所用时间之比为:
(3)通过连续相同的位移所用时间之比为:
【特别提醒】
(1)以上比例成立的前提是物体做初速度为零的匀加速直线运动。
(2)对于末速度为零的匀减速直线运动,可把它看成逆向的初速度为零的匀加速直线运动,应用比例关系,可使问题简化。
1.思考判断
(1)匀变速直线运动是加速度均匀变化的直线运动。( )
(2)匀变速直线运动的位移是均匀增加的。( )
(3)匀变速直线运动是加速度不变而速度均匀变化的直线运动。( )
(4)在匀变速直线运动中,中间时刻的速度一定小于该段时间内位移中点的速度。( )
×
×
√
√
2.(2023·重庆一诊)2022年北京冬奥会单板滑雪项目中的助滑道可简化为如图1所示的斜面模型。设一运动员从助滑道的顶端A点由静止开始匀加速下滑,最初2 s内的位移为10 m,则他滑到离顶端25 m的B点时的速度大约为( )
A.10 m/s B.13 m/s
C.16 m/s D.19 m/s
C
例3 如图4所示,一辆汽车在平直公路上做匀加速直线运动,从树A开始,在相等的时间内依次经过B、C、D、E 四棵树,已知树A、B 间距为s1,树D、E 间距为s2,则树B、D 间距为( )
解决匀变速直线运动的常用推论
角度
A
平均速度公式的应用
A.s1+s2 B.2s1+s2 C.s1+2s2 D.2(s1+s2)
角度
D
位移差公式的应用
例5 (2023·山东日照市高三月考)小金开车在石村村口A处停了一会,接着由静止开始匀加速直线行驶,途经B、C、D、E四个石墩,如图6所示。已知B到C、C到D、D到E的时间相等,B、C间距离为4 m,C、D间距离为6 m,根据以上信息,以下说法正确的是( )
图6
A.可以求出汽车通过C点时的速度大小
B.可以求出汽车的加速度大小
C.可以求得汽车在A、B之间的行驶时间
D.可以求得A、E之间的距离
例2 (多选)(2023·河北石家庄模拟)如图3所示,某飞机着陆时的速度v0=216 km/h,随后沿直线匀减速滑行到静止。从飞机着陆开始计时,该飞机在倒数第4 s内的位移为7 m,下列说法正确的是( )
图3
AC
A.该飞机的加速度大小为2 m/s2
B.该飞机着陆后5 s时的速度大小为40 m/s
C.该飞机在跑道上滑行的时间为30 s
D.该飞机在跑道上滑行的距离为1 800 m
跟踪训练
C
1.某质点做直线运动,位置随时间变化的关系式为x=100t-10t2+100 m,则对这个质点的运动描述正确的是( )
A.初速度为0
B.加速度为20 m/s2
C.在3 s末,瞬时速度为40 m/s
D.做匀加速直线运动
例1 (2022·江苏盐城模拟)近两年,交警将“礼让行人”作为管理重点,“斑马线前车让人”现已逐渐成为一种普遍现象,如图2所示。司机小明驾车以12 m/s的速度,在平直的城市道路上沿直线行驶。看到斑马线有行人后立即以大小为2 m/s2的加速度刹车,车停住时车头刚好碰到斑马线。等待行人10 s后(人已走过),又用了8 s时间匀加速至原来的速度。开始刹车时设为计时起点(即t=0),求:
图2
(1)车第3 s末的瞬时速度大小;
(2)车前10 s内的位移大小;
(3)从开始刹车到恢复至原来速度这段时间内,车的平均速度大小。
刹车陷阱
B
例4 (2023·广东珠海模拟)如图5为港珠澳大桥上四段110 m的等跨钢箱连续梁桥,若汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,则( )
角度
A.通过cd段的时间为t
B.通过ce段的时间为(2-)t
C.ae段的平均速度等于c点的瞬时速度
D.ac段的平均速度等于b点的瞬时速度
对点练2 匀变速直线运动的推论及应用
ABD
5.(多选)一质点做匀加速直线运动,第3 s内的位移是2 m,第4 s内的位移是2.5 m,那么以下说法中正确的是( )
A.这2 s内的平均速度是2.25 m/s
B.第3 s末的瞬时速度是2.25 m/s
C.质点的加速度是0.125 m/s2
D.质点的加速度是0.5 m/s2
跟踪训练
2.(2023·山东日照质检)一物体做匀加速直线运动,通过一段位移Δs所用时间为2t,紧接着通过下一段位移Δs所用时间为t。则物体运动的加速度大小为( )
C
3.如图7甲为游客排队滑冰滑梯的场景,在工作人员的引导下,每间隔相同时间从滑梯顶端由静止开始滑下一名游客,将某次拍到的滑梯上同时有多名游客的照片简化为如图乙所示,已知A、B和B、C间的距离分别为2.5 m和3.5 m,若游客在滑梯上做匀加速直线运动,求:
图7
(1)C、D间的距离;
(2)此刻A的上端滑道上还有几个人;
(3)此时A距滑道顶端的距离。
2.某短跑运动员完成100 m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中,该运动员用12 s跑完全程,已知该运动员在加速阶段的位移和匀速阶段的位移之比为1∶4,则该运动员在加速阶段的加速度为( )
A.2.0 m/s2 B.2.5 m/s2 C.3.0 m/s2 D.3.5 m/s2
B
3.高速公路的ETC电子收费系统如图1所示,ETC通道的长度是识别区起点到自动栏杆的水平距离。某汽车以5 m/s的速度匀速进入识别区,ETC天线用了0.3 s的时间识别车载电子标签,识别完成后发出“滴”的一声,司机发现自动栏杆没有抬起,于是采取制动刹车,汽车刚好没有撞杆。已知司机的反应时间为0.5 s,刹车的加速度大小为2.5 m/s2,则该ETC通道的长度约为( )
B
A.7 m B.9 m
C.11 m D.13 m
B
同课章节目录
