2024-2025学年勾股定理八年级数学上册第一章 勾股定理 基础测试卷(1)(含答案)
文档属性
| 名称 | 2024-2025学年勾股定理八年级数学上册第一章 勾股定理 基础测试卷(1)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-02 22:18:41 | ||
图片预览


文档简介
第一章基础测试卷(1)
考试时间:120分钟 满分:120分
题号 一 二 三 总分
得分
一、选择题
1.下列各组数中,不是勾股数的是( )
A.5,12,13 B.7,24,25
C.8,12,15 D.3k,4k,5k(k为正整数)
2.等腰直角三角形三边长的平方的比为( )
A.1:4:1 B.1:2:1
C.1:8:1 D.1:3:1
3.在△ABC中,BC=a,AB=c,AC=b,则不能作为判定△ABC是直角三角形的条件是( )
A.∠A=∠B-∠C B.∠A:∠B:∠C=1:4:3
C. a:b:c=7:24:25 D. a:b:c=4:5:6
4.已知x、y为正数,且 如果以x、y为两直角边长作一个直角三角形,那么以这个直角三角形的斜边长为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
5.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为 S 、S ,则 等于( )
A.2π B.π C.π/2 D.π4
6.如图所示,在正方形网格中,若每个小方格的边长均为1,则△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
7.如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC.△BCD的周长为13,则ED的长为( )
A.3 B.4 C.5 D.13
8.如图,方爷爷家屋后有一块长12m,宽8m的长方形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.9m B.7m C.5m D.3m
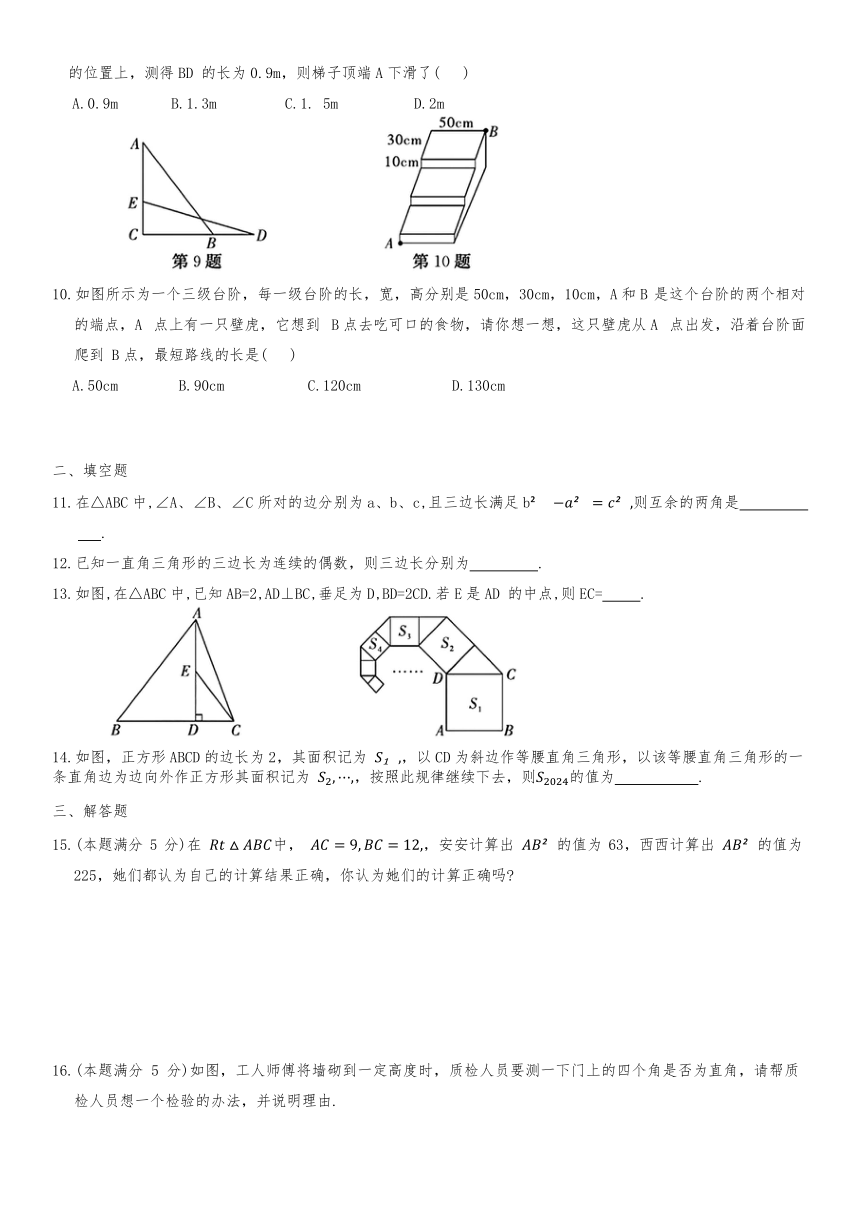
9.如图,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C的距离为1.5m,梯子滑动后停在DE的位置上,测得BD 的长为0.9m,则梯子顶端A下滑了( )
A.0.9m B.1.3m C.1. 5m D.2m
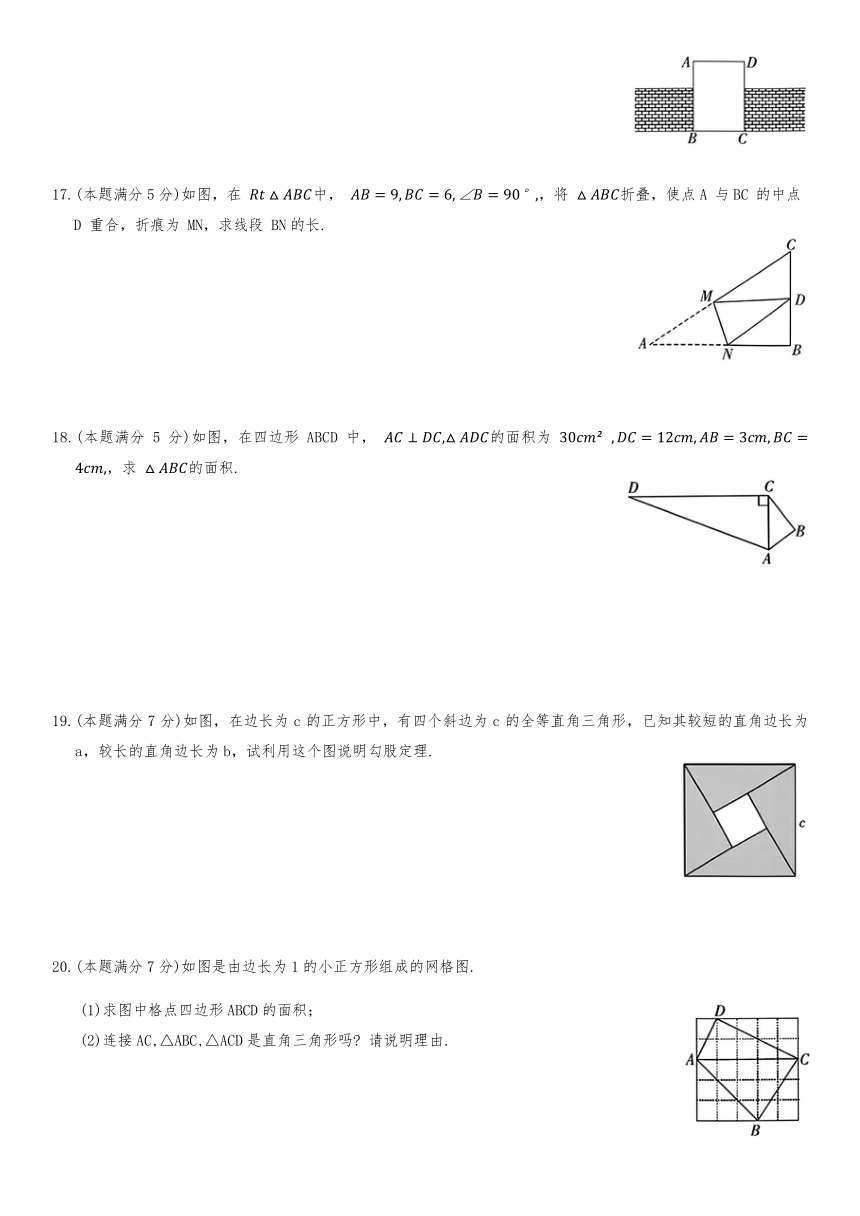
10.如图所示为一个三级台阶,每一级台阶的长,宽,高分别是50cm,30cm,10cm,A和B 是这个台阶的两个相对的端点,A 点上有一只壁虎,它想到 B点去吃可口的食物,请你想一想,这只壁虎从A 点出发,沿着台阶面爬到 B点,最短路线的长是( )
A.50cm B.90cm C.120cm D.130cm
二、填空题
11.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且三边长满足b 则互余的两角是 .
12.已知一直角三角形的三边长为连续的偶数,则三边长分别为 .
13.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD 的中点,则EC= .
14.如图,正方形ABCD的边长为2,其面积记为 ,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形其面积记为 ,按照此规律继续下去,则的值为 .
三、解答题
15.(本题满分5分)在 中, ,安安计算出 的值为63,西西计算出 的值为225,她们都认为自己的计算结果正确,你认为她们的计算正确吗
16.(本题满分5分)如图,工人师傅将墙砌到一定高度时,质检人员要测一下门上的四个角是否为直角,请帮质检人员想一个检验的办法,并说明理由.
17.(本题满分5分)如图,在 中, ,将 折叠,使点A 与BC 的中点D 重合,折痕为 MN,求线段 BN的长.
18.(本题满分5分)如图,在四边形ABCD中, 的面积为 ,求 的面积.
19.(本题满分7分)如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其较短的直角边长为a,较长的直角边长为b,试利用这个图说明勾股定理.
20.(本题满分7分)如图是由边长为1的小正方形组成的网格图.
(1)求图中格点四边形ABCD的面积;
(2)连接AC,△ABC,△ACD是直角三角形吗 请说明理由.
21.(本题满分7分)如图,四边形 BCDE为长方形, CD=2.求图中阴影部分的面积.
22.(本题满分7分)如图,小明在广场上先向东走10m,又向南走40m再向西走20m,又向南走 40m,再向东走 70m.求小明到达的终点与出发点的距离是多少.
23.(本题满分8分)有一辆装满货物的卡车,行进方向的截面视为矩形,高2.5米,宽1.6米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径(长方形的一边)为2米,长方形的另一条边长是2.3米.
(1)这辆卡车能否通过此桥洞 试说明你的理由.
(2)为了适应车流量的增加,想把桥洞改为双行道,并且要使行进方向截面的宽为1.2米,高为2.8米的卡车能安全通过,那么此桥洞的宽至少应增加到多少米
24.(本题满分 10 分)如图,在 中,CE 平分 ,CF 平分 且 交AC于M,若( 求 的值.
25.(本题满分12分)如图,桌子上放着一个长方体盒子,长、宽、高分别是12cm,8cm,30cm,在AB的中点C 处有一滴蜜糖,一只小虫从 E处沿盒子表面爬到C处去吃,求小虫爬行的最短路程.
第一章基础测试卷(1)
1.C 2.B 3.D 4.C 5.A 6.A 7.A 8.D 9.B 10.D
11. ∠A,∠C .12. 6,8,10 .13. 1 .14.
15.解:不完全正确;
当BC为斜边时,
当AB 为斜边时,
故答案为63 或225.
解:连接AC(图略),测量 AB,BC及AC 的长度,
利用勾股定理的逆定理可知,
若 则 是直角;
否则,∠ABC不是直角,类似的方法,
可以判断∠BCD,∠CDA,∠BAD 是否为直角.
解:设 ,
由折叠的性质可得
因为点D 是BC 的中点,
所以 3.
在 中,
解得 故线段 BN 的长为4.
解:在 Rt△ACD 中, 30cm .
因为DC=12cm,
所以AC=5cm.
因为
所以
所以△ABC是直角三角形,且∠ABC=90°,
所以
19.解:阴影部分的面积可用两种形式表示,
分别为c 或
所以
即
20.解:(1)四边形ABCD 的面积为
(2)△ACD 是直角三角形,△ABC 不是直角三角形.
理由:由图可得, 2 =13,
AD =1 +2 =5,CD =2 +4 =20,AC =5 =25.
因为AD
所以△ACD 是直角三角形,△ABC 不是直角三角形.
解:因为 AD=14,CD=2,
所以 AC=12.
因为 AB=13,∠ACB=90°,
所以
所以CB=5.所
解:如图,作AC⊥BC于点C.
因为AC=40+40 出发点10m=80(m),BC=70-20+10=60(m),
所以AB ,则AB=100m.
解:(1)能通过.
理由如下:如图①所示,当桥洞中心线两边各为0.8米时,
设卡车在半圆部分的高度为 xm.
则( 解得x=0.6.
因为2.5<2.3+0.6,所以能通过.
如图②所示,
故OA=1.3米,
所以桥洞的宽至少应增加到1.3×2=2.6(米).
解:因为CE 平分∠ACB,CF 平分∠ACD,
所以 ∠ACD,
即 ,
所以△EFC 为直角三角形,
又因为
所以∠ECB=∠MEC,∠DCF=∠CFM,
所以.
所以EM=CM=5,MC=MF=5,
所以EM=MF=5.
所以EF=10.由勾股定理可知
25.解:分三种情况.情况一:如图①,连接EC.
在 中,
由勾股定理,得
所以
情况二:如图②,连接 EC.根据勾股定理可求得
情况三:如图③,连接EC.根据勾股定理可求得
所以小虫爬行的最短路程是 25cm.
考试时间:120分钟 满分:120分
题号 一 二 三 总分
得分
一、选择题
1.下列各组数中,不是勾股数的是( )
A.5,12,13 B.7,24,25
C.8,12,15 D.3k,4k,5k(k为正整数)
2.等腰直角三角形三边长的平方的比为( )
A.1:4:1 B.1:2:1
C.1:8:1 D.1:3:1
3.在△ABC中,BC=a,AB=c,AC=b,则不能作为判定△ABC是直角三角形的条件是( )
A.∠A=∠B-∠C B.∠A:∠B:∠C=1:4:3
C. a:b:c=7:24:25 D. a:b:c=4:5:6
4.已知x、y为正数,且 如果以x、y为两直角边长作一个直角三角形,那么以这个直角三角形的斜边长为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
5.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为 S 、S ,则 等于( )
A.2π B.π C.π/2 D.π4
6.如图所示,在正方形网格中,若每个小方格的边长均为1,则△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
7.如图,在△ABC中,AB=AC=8,AB的垂直平分线DE分别交AB、AC于点E、D,BD=BC.△BCD的周长为13,则ED的长为( )
A.3 B.4 C.5 D.13
8.如图,方爷爷家屋后有一块长12m,宽8m的长方形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.9m B.7m C.5m D.3m
9.如图,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C的距离为1.5m,梯子滑动后停在DE的位置上,测得BD 的长为0.9m,则梯子顶端A下滑了( )
A.0.9m B.1.3m C.1. 5m D.2m
10.如图所示为一个三级台阶,每一级台阶的长,宽,高分别是50cm,30cm,10cm,A和B 是这个台阶的两个相对的端点,A 点上有一只壁虎,它想到 B点去吃可口的食物,请你想一想,这只壁虎从A 点出发,沿着台阶面爬到 B点,最短路线的长是( )
A.50cm B.90cm C.120cm D.130cm
二、填空题
11.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且三边长满足b 则互余的两角是 .
12.已知一直角三角形的三边长为连续的偶数,则三边长分别为 .
13.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD 的中点,则EC= .
14.如图,正方形ABCD的边长为2,其面积记为 ,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形其面积记为 ,按照此规律继续下去,则的值为 .
三、解答题
15.(本题满分5分)在 中, ,安安计算出 的值为63,西西计算出 的值为225,她们都认为自己的计算结果正确,你认为她们的计算正确吗
16.(本题满分5分)如图,工人师傅将墙砌到一定高度时,质检人员要测一下门上的四个角是否为直角,请帮质检人员想一个检验的办法,并说明理由.
17.(本题满分5分)如图,在 中, ,将 折叠,使点A 与BC 的中点D 重合,折痕为 MN,求线段 BN的长.
18.(本题满分5分)如图,在四边形ABCD中, 的面积为 ,求 的面积.
19.(本题满分7分)如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其较短的直角边长为a,较长的直角边长为b,试利用这个图说明勾股定理.
20.(本题满分7分)如图是由边长为1的小正方形组成的网格图.
(1)求图中格点四边形ABCD的面积;
(2)连接AC,△ABC,△ACD是直角三角形吗 请说明理由.
21.(本题满分7分)如图,四边形 BCDE为长方形, CD=2.求图中阴影部分的面积.
22.(本题满分7分)如图,小明在广场上先向东走10m,又向南走40m再向西走20m,又向南走 40m,再向东走 70m.求小明到达的终点与出发点的距离是多少.
23.(本题满分8分)有一辆装满货物的卡车,行进方向的截面视为矩形,高2.5米,宽1.6米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径(长方形的一边)为2米,长方形的另一条边长是2.3米.
(1)这辆卡车能否通过此桥洞 试说明你的理由.
(2)为了适应车流量的增加,想把桥洞改为双行道,并且要使行进方向截面的宽为1.2米,高为2.8米的卡车能安全通过,那么此桥洞的宽至少应增加到多少米
24.(本题满分 10 分)如图,在 中,CE 平分 ,CF 平分 且 交AC于M,若( 求 的值.
25.(本题满分12分)如图,桌子上放着一个长方体盒子,长、宽、高分别是12cm,8cm,30cm,在AB的中点C 处有一滴蜜糖,一只小虫从 E处沿盒子表面爬到C处去吃,求小虫爬行的最短路程.
第一章基础测试卷(1)
1.C 2.B 3.D 4.C 5.A 6.A 7.A 8.D 9.B 10.D
11. ∠A,∠C .12. 6,8,10 .13. 1 .14.
15.解:不完全正确;
当BC为斜边时,
当AB 为斜边时,
故答案为63 或225.
解:连接AC(图略),测量 AB,BC及AC 的长度,
利用勾股定理的逆定理可知,
若 则 是直角;
否则,∠ABC不是直角,类似的方法,
可以判断∠BCD,∠CDA,∠BAD 是否为直角.
解:设 ,
由折叠的性质可得
因为点D 是BC 的中点,
所以 3.
在 中,
解得 故线段 BN 的长为4.
解:在 Rt△ACD 中, 30cm .
因为DC=12cm,
所以AC=5cm.
因为
所以
所以△ABC是直角三角形,且∠ABC=90°,
所以
19.解:阴影部分的面积可用两种形式表示,
分别为c 或
所以
即
20.解:(1)四边形ABCD 的面积为
(2)△ACD 是直角三角形,△ABC 不是直角三角形.
理由:由图可得, 2 =13,
AD =1 +2 =5,CD =2 +4 =20,AC =5 =25.
因为AD
所以△ACD 是直角三角形,△ABC 不是直角三角形.
解:因为 AD=14,CD=2,
所以 AC=12.
因为 AB=13,∠ACB=90°,
所以
所以CB=5.所
解:如图,作AC⊥BC于点C.
因为AC=40+40 出发点10m=80(m),BC=70-20+10=60(m),
所以AB ,则AB=100m.
解:(1)能通过.
理由如下:如图①所示,当桥洞中心线两边各为0.8米时,
设卡车在半圆部分的高度为 xm.
则( 解得x=0.6.
因为2.5<2.3+0.6,所以能通过.
如图②所示,
故OA=1.3米,
所以桥洞的宽至少应增加到1.3×2=2.6(米).
解:因为CE 平分∠ACB,CF 平分∠ACD,
所以 ∠ACD,
即 ,
所以△EFC 为直角三角形,
又因为
所以∠ECB=∠MEC,∠DCF=∠CFM,
所以.
所以EM=CM=5,MC=MF=5,
所以EM=MF=5.
所以EF=10.由勾股定理可知
25.解:分三种情况.情况一:如图①,连接EC.
在 中,
由勾股定理,得
所以
情况二:如图②,连接 EC.根据勾股定理可求得
情况三:如图③,连接EC.根据勾股定理可求得
所以小虫爬行的最短路程是 25cm.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
